ГОУ СПО «Московский издательский полиграфический колледж им. Ивана Федорова»

Исследовательская работа по теме:

«Конус. Усеченный конус.»

Выполнили:

Студентка группы 1КТ2

Асташкина Валентина, Фролова Дарья

Проверила:

Епихина Е.В.

Москва

2012

Содержание:

1. Конус. Элементы

2. Усеченный конус

3. Элементы

4. Свойства

5. Свойства усеченного конуса

6. Формулы

5. Теоремы

5. Решение задач

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Конус.

Ко́нус (от др.-греч. κώνος «шишка») — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Также можно сказать, что это тело, полученное при вращении прямоугольного треугольника вокруг одного из его катетов. Далее будет рассматриваться именно этот случай, если не оговорено обратное. Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

рисунок 1     рисунок 2

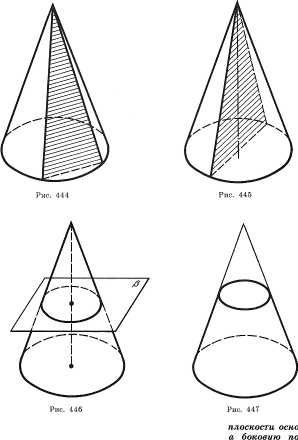
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1) Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис.2). Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

рисунок 3                                   рисунок 4   рисунок 5                                 рисунок 6

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4).

Усеченный конус.

Усечённый конус — часть конуса, заключенная между его основанием и сечением, параллельным основанию. Усеченный конус можно рассматривать как результат вращения равнобедренной трапеции вокруг её симметрии. При вращении основания трапеции описывают круги - основания усеченного конуса. Высота усеченного конуса - расстояние между основаниями.

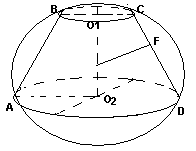
Круги с центрами О1 и О2 – верхнее и нижнее основания усеченного конуса, R r – радиусы оснований, АВ= L образующая ,α угол наклона образующе и плоскости нижнего основания.

Отрезок О1О2-высота. Трапеция АВСD – осевое сечение.

Боковая сторона трапеции называется образующей усеченного конуса; круги, полученные при вращении оснований трапеции, - основаниями усеченного конуса.

Развертка усеченного конуса представляет собой объединение части кругового кольца и двух кругов.

Свойства:

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания. Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.

• Телесный угол при вершине прямого кругового конуса равен

где  — угол раствора конуса (то есть угол между двумя противоположными образующими).

• Площадь боковой поверхности такого конуса равна

где  — радиус основания,  — длина образующей.

• Объем кругового конуса равен

• Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Св-ва усеченного конуса:

1)        В усеченный конус можно вписать шар тогда и только тогда, когда образующая равна сумме радиусов оснований.

2)        Вокруг усеченного конуса всегда можно описать шар.

Формулы:   Конус (рис. 1.19)

     Площадь боковой поверхности:

     Площадь полной поверхности:

     Объем:

     Усеченный конус (рис. 1.20)

     

     

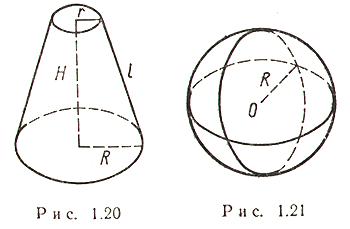
Боковая площадь поверхности круглого конуса, формула.

Боковая площадь поверхности круглого конуса равна произведению половины окружности основания (C) на образующую (l):

1.	S= 1 2  C l=π r l

(r - радиус вращения конуса; l - образующая конуса)

Полная площадь поверхности круглого конуса, формула.

Полная площадь поверхности круглого конуса равна сумме площадей боковой поверхности конуса и его основания. Основание конуса есть круг и его площадь вычисляется по формуле площади круга:

2.	S=π r l+π r2=π r (r+ l)

(r - радиус вращения конуса; l - образующая конуса)

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000