
- •1.1. Основные понятия, определения, допущения и принципы
- •Задача 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется… Варианты ответов:
- •3) Упругостью;
- •1.2. Модели прочностной надежности
- •1.3. Внутренние силы и напряжения
- •1.4. Перемещения и деформация
- •2.1. Продольная сила. Напряжения и деформации
- •2.2. Испытание конструкционных материалов на растяжение и сжатие
- •2.3. Механические свойства материалов
- •2.4. Расчеты стержней на прочность и жесткость
- •3.1. Чистый сдвиг. Расчет на сдвиг (срез)
- •3.2. Крутящий момент. Деформации и напряжения
- •3.3. Расчет на прочность при кручении
- •3.4. Расчет на жесткость при кручении
- •4.2. Виды напряженного состояния
- •4.3. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
- •4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
- •6. Плоский прямой изгиб
- •6.1. Поперечная сила, изгибающий момент и их эпюры
- •6.2. Напряжения в поперечном сечении стержня при плоском изгибе
- •6.3. Расчет балок на прочность
- •6.4. Перемещения при изгибе. Расчет балок на жесткость
- •Виды нагружения стержня
- •Пространственный и косой изгиб
- •Изгиб с растяжением-сжатием
- •Изгиб с кручением
- •Определение перемещений с помощью интегралов Мора. Правило Верещагина
- •Статическая неопределимость. Степень статической неопределенности
- •Метод сил
- •Расчет простейших статически неопределимых систем
- •Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
- •Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
- •9.3. Влияние условий закрепления концов стержня на величину критической силы
- •9.4. Устойчивость за пределом пропорциональности. Расчет сжатых стержней
- •5.1. Статические моменты. Центр тяжести плоской фигуры
- •5.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей
- •5.3. Главные оси и главные моменты инерции
- •Моменты инерции простых и сложных сечений
Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
Задача 9.2.1: Стержни изготовлены из одного материала, имеют одинаковую длину, размеры и форму поперечного сечения. Критическая сила имеет наибольшее значение для стержня, показанного на рисунке… При решении учитывайте, что напряжения в стержнях не превышают предел пропорциональности.
1) ;
2)
;
2)![]() ;
;
3) ;
4)
;
4) .
.
Решение:
1) Ответ неверный! Необходимо проанализировать формулу для определения критической силы в зависимости от коэффициента приведения длины .
2) Ответ неверный! Для данной схемы значение критической силы будет наименьшим.
3) Ответ
верный.
Формула для определения критической
силы при различных вариантах закрепления
сжатого стержня имеет вид
 ,
где
− коэффициент
приведения длины, учитывающий условия
опирания стержня. На рисунке показано
несколько видов закрепления стержня и
значения коэффициента
.
,
где
− коэффициент
приведения длины, учитывающий условия
опирания стержня. На рисунке показано
несколько видов закрепления стержня и
значения коэффициента
.
 Подставим
значение коэффициента приведения длины
в выражение для определения критической
силы. Из сопоставления значений
Подставим
значение коэффициента приведения длины
в выражение для определения критической
силы. Из сопоставления значений
![]() видно,
что наибольшее значение будет для
стержня на рис. 3).
видно,
что наибольшее значение будет для
стержня на рис. 3).
4) Ответ
неверный!
Значение критической силы зависит при
прочих равных условиях от условий
закрепления стержня. При шарнирном
опирании коэффициент приведения длины
,
а для схемы 3)
имеем
![]() .
Из анализа формулы для определения
критической силы следует, что, чем меньше
значение
,
тем больше значение критической силы.
.
Из анализа формулы для определения
критической силы следует, что, чем меньше
значение
,
тем больше значение критической силы.
Задача 9.2.2:
Граница применимости обобщенной формулы
Эйлера
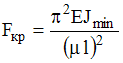 определяется...
определяется...
1)
величиной жесткости поперечного сечении
стержня на изгиб
![]() ;
;
2) физико-механическими свойствами материала сжимаемого стержня;
3)
неравенством
![]() ;
4) неравенством
;
4) неравенством
![]() .
.
Решение:
1) Ответ
неверный!
В формулу Эйлера
 действительно
входит выражение минимальной жесткости
поперечного сечения стержня на изгиб.
Это связано с тем, что потеря устойчивости
сжатого стержня связана с изгибом,
происходящим в плоскости с минимальной
жесткостью. Однако данная величина не
является критерием для определения
границы применимости использования
формулы Эйлера.
действительно
входит выражение минимальной жесткости
поперечного сечения стержня на изгиб.
Это связано с тем, что потеря устойчивости
сжатого стержня связана с изгибом,
происходящим в плоскости с минимальной
жесткостью. Однако данная величина не
является критерием для определения
границы применимости использования
формулы Эйлера.
2) Ответ
верный.
Известно, что применимость формулы
Эйлера ограничена неравенством
![]() .
.
 ,
или
,
или
 ,
здесь
,
здесь
 .
Тогда минимальное значение гибкости
.
Тогда минимальное значение гибкости
 ,
где Е –
модуль упругости,
–
предел пропорциональности.
Таким
образом, граница применимости формулы
Эйлера определяется физико-механическими
свойствами материала.
,
где Е –
модуль упругости,
–
предел пропорциональности.
Таким
образом, граница применимости формулы
Эйлера определяется физико-механическими
свойствами материала.
3) Ответ
неверный!
Неравенство предполагает, что напряжения,
возникающие в момент потери устойчивости
стержня, превышают значение предела
пропорциональности материала, из
которого изготовлен стержень. Однако
формула Эйлера получена в предположении
малости перемещений и отсутствия
пластических деформаций. Следовательно,
границей применимости обобщенной
формулы Эйлера является неравенство
![]() .
.
4) Ответ
неверный!
Неравенство предполагает наличие
верхней и нижней границы применимости
формулы Эйлера. Однако существует только
нижняя граница, определяемая формулой
 .
Формула получена с использованием
соотношения
.
.
Формула получена с использованием
соотношения
.
Задача 9.2.3: Стержень круглого сечения диаметром нагружен силой . При увеличении диаметра в два раза значение критической силы увеличится в ________ раз (-а). При решении учитывайте, что нормальные напряжения в стержне не превышают предела пропорциональности.
1) 16; 2) 8; 3) 2; 4) 32.
Решение:
1) Ответ
верный.
Выражение критической силы сжатого
стержня имеет вид
.
При
изменении размеров поперечного сечения
зависит
от минимального значения осевого момента
инерции сечения
![]() .
При значении диаметра, равного d,
получим
.
При значении диаметра, равного d,
получим
 .
С увеличением диаметра стержня в два
раза имеем
.
С увеличением диаметра стержня в два
раза имеем
 .
Следовательно,
значение критической силы увеличится
в 16 раз.
.
Следовательно,
значение критической силы увеличится
в 16 раз.
2) Ответ
неверный!
Критическая сила пропорциональна
минимальному осевому моменту инерции
сечения, который определяется для
круглого сечения по формуле
 .
Диаметр стоит не в третьей, а четвертой
степени.
.
Диаметр стоит не в третьей, а четвертой
степени.
3) Ответ неверный! Значение критической силы не изменяется пропорционально диаметру сечения.
4) Ответ неверный! Допущена ошибка при возведении числа в степень.
Задача 9.2.4: Использование формулы Эйлера является корректным при выполнении неравенства …
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
Решение:
1) Ответ
неверный!
Формула Эйлера получена в предположении,
что напряжение в стержне в момент потери
устойчивости не превышает предела
пропорциональности
 а
не предела текучести
а
не предела текучести
![]() .
.
2) Ответ
неверный!
Формула Эйлера получена в предположении,
что значение напряжения в стержне в
момент потери устойчивости не превышает
предела пропорциональности![]() или
или
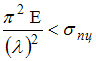 ,
а не предела текучести
.
Следовательно,
.
,
а не предела текучести
.
Следовательно,
.
3) Ответ
неверный!
Величина
 определяет
нижнюю границу значения гибкости для
применимости формулы Эйлера. Верхняя
граница не регламентируется. Данное
неравенство предполагает использование
формулы Эйлера для расчета стержней,
имеющих гибкость меньше данной величины.
Использование формулы Эйлера для
стержней малой гибкости приведет к
получению значений
определяет
нижнюю границу значения гибкости для
применимости формулы Эйлера. Верхняя
граница не регламентируется. Данное
неравенство предполагает использование
формулы Эйлера для расчета стержней,
имеющих гибкость меньше данной величины.
Использование формулы Эйлера для
стержней малой гибкости приведет к
получению значений
![]() ,
превышающих предел текучести и предел
прочности, что крайне опасно по своим
последствиям.
,
превышающих предел текучести и предел
прочности, что крайне опасно по своим
последствиям.
4) Ответ
верный.
Формула Эйлера
 получена
в предположении, что нормальное напряжение
в стержне, в момент потери устойчивости,
не превышает предела
пропорциональности:
получена
в предположении, что нормальное напряжение
в стержне, в момент потери устойчивости,
не превышает предела
пропорциональности:

 ,
, ,
где
,
где![]() – минимальный
радиус инерции поперечного сечения
стержня;
− гибкость стержня.
Таким
образом,
.
– минимальный
радиус инерции поперечного сечения
стержня;
− гибкость стержня.
Таким
образом,
.
Тема:
Формула Эйлера для критической силы
сжатого стержня и пределы ее
применимости
 Стержень
круглого сечения диаметром d,
длиной l сжимается
силой F.
При увеличении линейных размеров l и d в
два раза значение критической силы, при
прочих равных условиях, ___________. При
решении учитывать, что напряжения в
сжатом стержне не превышают предела
пропорциональности.
Стержень
круглого сечения диаметром d,
длиной l сжимается
силой F.
При увеличении линейных размеров l и d в
два раза значение критической силы, при
прочих равных условиях, ___________. При
решении учитывать, что напряжения в
сжатом стержне не превышают предела
пропорциональности.
|
|
|
увеличится в 4 раза |
|
|
|
не изменится |
|
|
|
уменьшится в 2 раза |
|
|
|
увеличится в 8 раз |
Решение:
Для
определения критической силы сжатого
стержня, когда напряжения не превышают
предела пропорциональности, воспользуемся
формулой Эйлера  где
для
круглого сечения определяется по
формуле
где
для
круглого сечения определяется по
формуле  При
увеличении линейных размеров l и d в
два раза значение критической силы
увеличится в 4 раза.
При
увеличении линейных размеров l и d в
два раза значение критической силы
увеличится в 4 раза.
Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Возможность применения формулы Эйлера для определения критической силы сжатого стержня, изготовленного из заданного материала, устанавливается по величине …
|
|
|
гибкости |
|
|
|
площади сечения |
|
|
|
длины |
|
|
|
радиуса инерции сечения |
Решение:
Формула
Эйлера для определения критической
силы сжатого стержня справедлива, если
напряжения в стержне не превышают
предела пропорциональности, то
есть  или
или  где
− гибкость
стержня.
Если из неравенства выразить
гибкость, то условие применения формулы
Эйлера получит вид
где
− гибкость
стержня.
Если из неравенства выразить
гибкость, то условие применения формулы
Эйлера получит вид  Следовательно,
величина гибкости устанавливает
возможность применения формулы Эйлера.
Следовательно,
величина гибкости устанавливает
возможность применения формулы Эйлера.
Тема:
Формула Эйлера для критической силы
сжатого стержня и пределы ее применимости
Для
стержня с шарнирно-опертыми концами
значению критической силы  соответствует
изгиб стержня по …
соответствует
изгиб стержня по …
|
|
|
полуволне синусоиды |
|
|
|
квадратичной параболе |
|
|
|
дуге окружности |
|
|
|
синусоиде |
Решение:
При
выводе формулы Эйлера пользуются
приближенным дифференциальным уравнением
изогнутой оси стержня. После интегрирования
и выполнения граничных условий получают
наименьшее значение критической силы  и
форму изогнутой оси стержня в виде
полуволны синусоиды
и
форму изогнутой оси стержня в виде
полуволны синусоиды ![]() с
максимальным прогибом А.
с
максимальным прогибом А.
Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Формула Эйлера для определения критической силы применима, если напряжения в сжатом стержне не превышают …
|
|
|
предела пропорциональности |
|
|
|
предела упругости |
|
|
|
предельного напряжения |
|
|
|
предела текучести |
Решение:
При
выводе формулы Эйлера использовалось
приближенное дифференциальное уравнение
изогнутой оси стержня. Дифференциальное
уравнение, в свою очередь, было получено
на допущении, что нормальное напряжение
прямо пропорционально линейной
деформации ![]() .
Закон Гука выполняется до предела
пропорциональности. Поэтому формула
Эйлера для определения критической
силы применима, если напряжения в сжатом
стержне не превышают предела
пропорциональности.
.
Закон Гука выполняется до предела
пропорциональности. Поэтому формула
Эйлера для определения критической
силы применима, если напряжения в сжатом
стержне не превышают предела
пропорциональности.
