- •*Пружинный маятник
- •*Математический маятник
- •Характеристики затухающих колебаний
- •Затухающие колебания в электрическом контуре
- •Затухающий гармонический осциллятор
- •Консервативный гармонический осциллятор
- •[Править]Резонанс
- •Типы волн: продольные и поперечные, плоские, сферические.
- •Волновое уравнение.
- •Вектор Пойнтинга.
- •Если отверст. Открыв. Четное число зон Френеля то в т. P наблюд. Min, если нечетное – то max.
Если отверст. Открыв. Четное число зон Френеля то в т. P наблюд. Min, если нечетное – то max.
Пусть на пути сферич. фронта свет. волны распол. круглый непрозрачный диск, к-й закрыв. 1-е m зон Френеля.
A= Am+1-Am+2+Am+3-Am+4+…=Am+1/2+(Am+1/2-Am+2+ Am+3/2)+(Am+3/2-…=Am+1/2
Видно что в т.P всегда наблюд. max. Расчитаем радиус зон Френеля.
rm2=a2-(a-h)2=(b-m/2)2-(b+h)2, пренебрегая величинами порядка 2 окончательно получаем
rm=(abm/(a+b))- сферический фронт свет. волны
rm=lima(abm/(a+b))=(bm) т.е. rm=(bm)-плоский фронт свет. волны.
Френель предложил объединил симметрич. т-ки световой волны в зоны выбирая конфигурацию и размеры зоны такие что разность хода лучей от краев 2-х соседних зон от т-ки наблюдений была бы равна /2 и след-но от краев 2-х сосдних волн приход. в т-ку наблюдения в противофазе и при наложении др. на др. ослабивают.
18)Дифракция Фраунгофера
Если перед линзой расположена диафрагма в виде узкой щели ширины D, то расчет для дифракционной картины Фраунгофера не представляет труда (см. главу 1.2). В этом случае для распределения интенсивности в дифракционной картине получается выражение
|
|
(4.2) |
Здесь ![]() –
угловая координата плоскости наблюдения.
При наблюдении дифракции в геометрически
сопряженной плоскости линейная
координата
–
угловая координата плоскости наблюдения.
При наблюдении дифракции в геометрически
сопряженной плоскости линейная
координата ![]() связана
(в случае малых углов) с угловой
координатой
соотношением:
связана
(в случае малых углов) с угловой
координатой
соотношением: ![]() .
(или :
.
(или :![]() для
случая рис. 4.2).
для
случая рис. 4.2).
Распределение ![]() имеет
главный максимум при
имеет
главный максимум при ![]() и
эквидистантно расположенные нули
при
и
эквидистантно расположенные нули
при ![]() ,
где m –
целое число. Значительная часть энергии
света, прошедшего через щель, локализуется
в главном дифракционном максимуме,
угловая полуширина которого равна
,
где m –
целое число. Значительная часть энергии
света, прошедшего через щель, локализуется
в главном дифракционном максимуме,
угловая полуширина которого равна ![]() .
Интенсивность соседнего максимума
составляет приблизительно 5 % от
интенсивности в центре дифракционной
картины. Этот случай представляет для
дифракционной теории оптических
инструментов чисто методический
интерес, поскольку, как правило, входные
апертуры имеют вид круглых отверстий.
Расчет фраунгоферовой дифракции на
круглом отверстии оказывается достаточно
громоздким и приводит к бесселевым
функциям первого порядка
.
Интенсивность соседнего максимума
составляет приблизительно 5 % от
интенсивности в центре дифракционной
картины. Этот случай представляет для
дифракционной теории оптических
инструментов чисто методический
интерес, поскольку, как правило, входные
апертуры имеют вид круглых отверстий.
Расчет фраунгоферовой дифракции на
круглом отверстии оказывается достаточно
громоздким и приводит к бесселевым
функциям первого порядка ![]() .
.
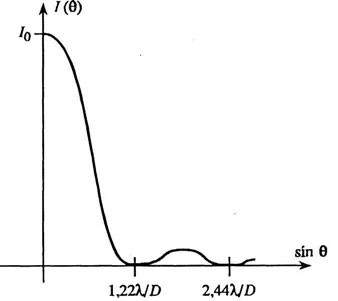
Распределение интенсивности света при дифракции Фраунгофера на круглом отверстии диаметра D выражается формулой
|
|
(4.3) |
Распределения (4.2) и (4.3) очень похожи друг на друга. Картина дифракции на круглом отверстии имеет вид концентрических колец. Центральное светлое пятно носит название пятна Эйри. Интенсивность в максимуме первого светлого кольца составляет приблизительно 2 % от интенсивности в центре пятна Эйри. Распределение (4.3) показано на рис. 4.3.
|
|
При оценке разрешающей способности оптических инструментов важно знать размер центрального дифракционного максимума. Угловой радиус пятна Эйри выражается соотношением
|
|
Разрешающая способность системы объектив + светочувствительный элемент приближенно определяется по формуле:
![]() ,
,
где ![]() –
разрешающая сила объектива в линиях
на 1 мм;
–
разрешающая сила объектива в линиях
на 1 мм; ![]() —
разрешающая сила светочувствительного
элемента в линиях на 1 мм. Данная формула
непригодна для матричных фотоприемников
в связи с их дискретным характером.
—
разрешающая сила светочувствительного
элемента в линиях на 1 мм. Данная формула
непригодна для матричных фотоприемников
в связи с их дискретным характером.
19)Дифракционная решетка. ЕЕ разрешающая способность.
Система параллельных щелей, разделенных непрозрачными промежутками, называется дифракционной решеткой. Расстояние между щелями d=a+b называют периодом решетки.
Рассмотрим диф. реш. d=a+b, перио или пост. диф. Лучи дифрак. от двух щелей имеют опред. разность хода Δ=sinφ, δ=2πΔ/λ=2πdsinφ/ λ.
В д.р. кроме дифрак. от каждой щели
происходит сложение кол–й от различ.
щелей решетки, т.е. мы имеем дело с
многомерной интерполяцией.
д.р. кроме дифрак. от каждой щели
происходит сложение кол–й от различ.
щелей решетки, т.е. мы имеем дело с
многомерной интерполяцией.
Разрешающей способностью спектрального прибора принято называть отношение
|
|
(3.9) |
где ![]() –
минимальный интервал между двумя
близкими спектральными линиями, при
котором они могут быть разрешены, то
есть отделены одна от другой. В качестве
критерия разрешения используется
обычно критерий
разрешения Рэлея.
Спектральные линии с близкими
значениями
–
минимальный интервал между двумя
близкими спектральными линиями, при
котором они могут быть разрешены, то
есть отделены одна от другой. В качестве
критерия разрешения используется
обычно критерий
разрешения Рэлея.
Спектральные линии с близкими
значениями ![]() и
и ![]() считаются
разрешенными, если главный максимум
дифракционной картины для одной
спектральной линии совпадает по своему
положению с первым дифракционным
минимумом для другой спектральной
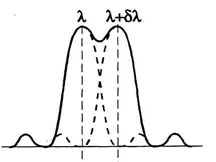
линии. Рис. 3.4. поясняет критерий
Рэлея.
считаются
разрешенными, если главный максимум
дифракционной картины для одной
спектральной линии совпадает по своему
положению с первым дифракционным
минимумом для другой спектральной
линии. Рис. 3.4. поясняет критерий
Рэлея.
|
Рисунок 3.4. Кретерий спектрального разрешения Рэлея. |
Так как спектральные линии, изображенные на рис. 3.4, некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис. 3.4). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея.
Для разрешающей способности дифракционной решетки легко получить из выражения (3.3):
|
|
20) Поляризация света. Закон Малюса. Закон Брюстера. Формулы Френеля.
Опыт показывает, что при падении на диэлектрик (вода, стекло) отраженный и преломленный лучи всегда частично поляризованы. Степень поляризации при этом зависит от угла падения и показателя преломления отражающей среды. При этом отраженный луч частично поляризован в плоскости, перпендикулярной плоскости падения, а преломленный - в плоскости падения. Условие полной поляризации состоит в том, чтобы угол между отраженным и преломленным лучами был равен π/2, т.е. чтобы n=sin i0/sin r= sin i0/cos i0=tg i0. Это соотношение называют законом Брюстера. Этот закон объясняется тем, что отраженный преломленный лучи представляют собой вторичное излучение, возбужденное падающей волной. Электроны колеблются в направлении вектора Е. Однако электрический диполь не излучает в этом направлении, максимум излучения приходится на перпендикулярное направление.
Если
на анализатор падает поляризованный
луч, плоскость поляризации которого
составляет угол ![]() с
плоскостью поляризации анализатора,
то интенсивность прошедшего сквозь
анализатора луча определяет закон
Малюса.
с
плоскостью поляризации анализатора,
то интенсивность прошедшего сквозь
анализатора луча определяет закон
Малюса.
закон Малюса :
![]() ,
,
где Io - интенсивность луча, прошедшего анализатор и поляризатор, когда их плоскости поляризации параллельны; I - интенсивность луча, выходящего из анализатора, без учета потерь в анализаторе в результате поглощения и рассеяния света.
Согласно формуле Френеля угол падения луча 1, угол отражения 2 и угол преломления 3 связаны следующими уравнениями:
1 = 2 n1sin1 = n2sin3
Отражательная способность границы раздела сред для лучей с параллельной и перпендикулярной поляризацией R|| и R, а также пропускательная способность границы сред T и T описывается выражениями:

Для луча, падающего нормально к границе раздела, исчезает различие между перпендикулярной и параллельной компонентами, т.е.
![]()
21) Внешний фотоэффект. Основные закономерности.Формула энштейна.Фотоны.
Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любогоэлектромагнитного излучения). В конденсированныхвеществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Законы фотоэффекта:
Формулировка 1-го закона фотоэффекта: количествоэлектронов, вырываемых светом с поверхности металла за единицу времени на данной частоте, прямо пропорционально световому потоку, освещающему металл.
Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
3-ий
закон фотоэффекта: для
каждого вещества существует красная
граница фотоэффекта, то есть минимальная
частота света ![]() (или
максимальная длина волны λ0),
при которой ещё возможен фотоэффект,
и если
(или
максимальная длина волны λ0),
при которой ещё возможен фотоэффект,
и если ![]() ,
то фотоэффект уже не происходит.
,
то фотоэффект уже не происходит.
Теоретическое
объяснение этих законов было дано
в 1905
году Эйнштейном.
Согласно ему, электромагнитное излучение
представляет собой поток отдельных
квантов (фотонов)
с энергией hν каждый, где h — постоянная
Планка.
При фотоэффекте часть падающего
электромагнитного излучения от
поверхности металла отражается, а часть
проникает внутрь поверхностного слоя
металла и там поглощается. Поглотив
фотон, электрон получает от него энергию
и, совершая работу выхода, покидает
металл: ![]() ,
где
,
где ![]() —
максимальная кинетическая энергия,
которую может иметь электрон при вылете
из металла.
—
максимальная кинетическая энергия,
которую может иметь электрон при вылете
из металла.
Фото́н (от др.-греч. φῶς, род. пад. φωτός, «свет») — элементарная частица, квантэлектромагнитного излучения (в узком смысле —света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Электрический заряд фотона также равен нулю.
22)Давление света.Опыты Лебедева
Давление света открыто русским ученым П.Н. Лебедевым в 1901 году. В своих опытах он установил, что давление света зависит от интенсивности света и от отражающей способности тела. В опытах была использована вертушка, имеющая черные и зеркальные лепестки, помещенная в вакуумированную колбу (рис. 2.10).
 Рис.
2.10
Рис.
2.10
Вычислим величину светового давления.
На тело площадью S падает световой поток с энергией , где N – число квантов (рис. 2.11).
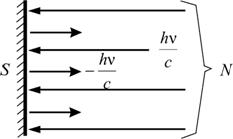 Рис.
2.11
Рис.
2.11
KN квантов отразится от поверхности; (1 – K)N– поглотится (рис. 2.10), K– коэффициент отражения.
Каждый поглощенный фотон передаст телу импульс:
|
. |
(2.7.5) |
|
Каждый отраженный фотон передаст телу импульс:
|
|
(2.7.6) |
|
т.к. .
В единицу времени все N квантов сообщают телу импульс р:
|
|
(2.7.7) |
|
Т.к. фотон обладает импульсом, то импульс, переданный телу за одну секунду, есть сила давления – сила, отнесенная к единице поверхности.
Тогда давление , или
![]()
где J – интенсивность излучения. Т. е. давление света можно рассчитать:
|
|
(2.7.8) |
|
·
если тело зеркально отражает, то K =
1 и ![]()
· если полностью поглощает (абсолютно черное тело), то K = 0 и , т.е. световое давление на абсолютно черное тело в два раза меньше, чем на зеркальное.
23)Явление Комптона.
Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучениявследствие упругого рассеивания его электронами. Обнаружен американским физиком Артуром Комптоном в1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытие Нобелевскую премию по физике.
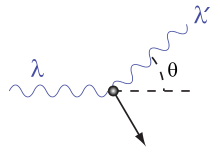
Иллюстрация к эффекту Комптона
При
рассеяниифотона на
покоящемсяэлектроне частоты
фотона ![]() и
и ![]() (до
и после рассеяния соответственно)
связаны соотношением:
(до
и после рассеяния соответственно)
связаны соотношением:
![]()
где ![]() —
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
—
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
Перейдя к длинам волн:
![]()
где ![]() — комптоновская
длина волны электрона.
— комптоновская
длина волны электрона.
24)Тепловое излучение. Законы теплового излучения. Гипотеза планка. формула планка.
Теплово́е излуче́ние — электромагнитное излучение с непрерывнымспектром, испускаемое нагретыми телами за счёт их тепловой энергии.
Примером теплового излучения является свет от лампы накаливания.
Мощность теплового излучения объекта, удовлетворяющего критериям абсолютно чёрного тела, описывается законом Стефана — Больцмана.
Отношение излучательной и поглощательной способностей тел описывается законом излучения Кирхгофа.
Тепловое излучение является одним из трёх элементарных видов переноса тепловой энергии (помимо теплопроводности и конвекции).
Равновесное излучение — тепловое излучение, находящееся втермодинамическом равновесии с веществом.
Тепловое излучение происходит по всему спектру частот от нуля до бесконечности
Интенсивность теплового излучения неравномерна по частотам и имеет явно выраженный максимум при определенной частоте
C ростом температуры общая интенсивность теплового излучения возрастает
C ростом температуры максимум излучения смещается в сторону больших частот (меньших длин волн)
Тепловое излучение характерно для тел независимо от их агрегатного состояния
Отличительным свойством теплового излучения является равновесный характер излучения. Это значит что если мы поместим тело в термоизолированный сосуд, то количество поглощаемой энергии всегда будет равно количеству испускаемой энергии.
Гипо́теза Пла́нка — гипотеза, выдвинутая 14 декабря 1900 года Максом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию
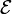 ,
пропорциональной частоте ν излучения:
,
пропорциональной частоте ν излучения: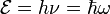
где h или
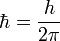 —
коэффициент пропорциональности,
названный впоследствии постоянной
Планка.
—
коэффициент пропорциональности,
названный впоследствии постоянной
Планка.
Формула
Планка —
выражение для спектральной плотности
мощности излучения абсолютно чёрного
тела, которое было получено Максом
Планком. Для плотности энергии
излучения ![]() :
:
![]()