Характеристики затухающих колебаний

        Чем меньше силы трения в системе, тем медленнее затухают колебания, тем лучше колебательная система. Для характеристики качества колебательной системы вводится ряд параметров:

t = 1/b - время релаксации затухающих колебаний (за t  амплитуда уменьшается в e раз).   

   - логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.

   - добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времени t.

8)Затухающие колебания в электрическом контуре. Параметры затухающих колебаний. Критическое сопротивление.

Затухающие колебания в электрическом контуре

        Рассмотрим, например, электрический колебательный контур с активным сопротивлением:

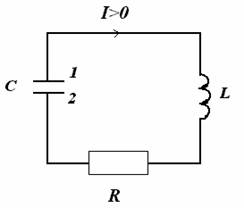
        В отличие от ранее рассмотренного идеального контура наличие сопротивления обеспечивает потери электромагнитной энергии в контуре, что ведет к затуханию колебаний. Закон Ома для контура 1-L-R-2 запишется следующим образом (обозначения те же, что и ранее): 

        Сделав в этом уравнении те же подстановки, получим:

     или     

где           и     

        Решением канонического дифференциального уравнения затухающих колебаний величины x является:

        В этом уравнении:   - амплитуда затухающих колебаний; j₀ - начальная амплитуда;  - циклическая частота затухающих колебаний (слово "циклическая" будем для краткости обычно опускать, когда и так ясно, о какой частоте идет речь). Период затухающих колебаний T = 2p/w.

        Затухающие колебания формально не попадают под определение периодических колебаний, - каждое последующее колебание не в точности повторяет предыдущее (см. график). Поэтому - опять же формально - нельзя пользоваться понятиями, введенными для периодических колебаний (частота, период). Чтобы обойти эту логическую неувязку, w и T определяют как условную частоту и условный период, а затем про "условные" слова тут же забывают.

График

посмотреть колебания волны на осциллографе

        Частота затухающих колебаний, разумеется, не может быть отрицательной, поэтому формулы для x и wсправедливы при b < w₀. Если же мы имеем случай b > w₀, или b = w₀, что означает большое трение в системе, то колебаний не происходит; система, будучи выведенной из равновесия, возвращается к равновесному состоянию без колебаний. Такое движение называется апериодическим (то есть не периодическим, см. график, на котором показаны возможные апериодические движения а и б).

График

Для описания затухающих колебаний используются: время релаксации, коэффициент затухания, логарифмический коэффициент затухания, добротность системы и т.д.

1. Время релаксации t.

Временем релаксации называют промежуток времени, за который амплитуда затухающих колебаний уменьшается в  е раз (е - основание натуральных логарифмов).

2. Коэффициент затухания s.

Коэффициентом затухания называют физическую величину,  обратно пропорциональную времени релаксации:

s = 1/τ  или        s =b/2m.

(6.67)

    3. Логарифмический   декремент   затухания l

Логарифмическим декрементом затухания называют натуральный логарифм отношения амплитуды в данный момент времени к амплитуде колебания спустя период.

Действительно,

.

(6.68)

Логарифмический декремент затухания прямо пропорционален произведению коэффициента затухания и  периоду затухающих колебаний.

 

4.  Добротность системы Q.

Из формулы (6.65) параграфа 6.17 следует, что круговая частота частицы (шарика на пружине - осциллятора) с учетом сил сопротивления меньше собственной частоты гармонических колебаний осциллятора без учета сил трения.

Следовательно, период затухающих колебаний  Т, наоборот, больше периода собственных колебаний Т₀. Причина ясна. Вязкое трение тормозит движение шарика.

 Как уже отмечалось выше, при  наличии трения энергия осциллятора уменьшается, превращаясь в тепловую энергию, рассеиваясь в окружающей среде.

Физическую величину, характеризующую потери энергии при затухающих колебаниях, называют добротностью.

Добротность Q физической системы можно найти по формуле

(6.69)

Как известно, энергия прямо пропорциональна квадрату амплитуды, тогда формулу (6.69) можно представить в следующем  виде:

(6.70)

где  А(t)=A_oе ^- st .

При малых колебаниях физической системы (мало сопротивление и, следовательно, малы потери энергии) добротность можно найти по формуле (Т® Т₀):

Q=ω_o/2σ       или     Q »π/σ.

Критическое сопротивление контура – это такое

сопротивление, при котором в контуре начинается апериодический разряд. В

этом случае колебания в контуре отсутствуют, заряд на обкладках

конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя

один раз положение равновесия, заряд конденсатора в итоге монотонно будет

убывать до нуля.

9)Сложение двух коллинеарных колебаний одинаковой частоты.

1. Сложение колебаний одного напpавления. Сложим два колебания одинаковой частоты, но pазличных фаз и амплитуд.                                                                                                                             (4.40)         Пpи наложении колебаний дpуг на дpуга          Введем новые паpаметpы А и j согласно уpавнениям:                                                                                                                             (4.42) Система уpавнений (4.42) легко pешается. (4.43)                                                                                                                             (4.44)         Таким обpазом, для х окончательно получаем уpавнение                                                                                                                             (4.45)         Итак, в pезультате сложения однонапpавленных колебаний одинаковой частоты получаем гаpмоническое (синусоидальное) колебание, амплитуда и фаза котоpого опpеделяется фоpмулами (4.43) и (4.44). 

10) Вынужденные колебания гармонического осциллятора. Дифференциальное уравнение вынужденных колебаний. Резонанс.