
- •*Пружинный маятник
- •*Математический маятник
- •Характеристики затухающих колебаний
- •Затухающие колебания в электрическом контуре
- •Затухающий гармонический осциллятор
- •Консервативный гармонический осциллятор
- •[Править]Резонанс
- •Типы волн: продольные и поперечные, плоские, сферические.
- •Волновое уравнение.
- •Вектор Пойнтинга.
- •Если отверст. Открыв. Четное число зон Френеля то в т. P наблюд. Min, если нечетное – то max.
1)Общая характеристика колебаний.Классификация колебаний.
Колеба́ния — повторяющийся в той или иной степени во временипроцесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращениемэнергии одной формы проявления в другую форму.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.

2)Незатухающие гармонические колебания. Параметры гармонических колебаний. Дифференциальное уравнение г.к. Энергия колебаний.
НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянной амплитудой.
Важным частным случаем периодических колебаний являются гармонические колебания, т.е. такие изменения физической величины, которые идут по закону
![]()
где
![]() .
Из курса математики известно, что
функция вида (1) меняется в пределах от
А до -А , и что наименьший положительный
период у нее
.
Из курса математики известно, что
функция вида (1) меняется в пределах от
А до -А , и что наименьший положительный
период у нее
![]() .
Поэтому гармоническое колебание вида
(1) происходит с амплитудой А и периодом
.
Поэтому гармоническое колебание вида
(1) происходит с амплитудой А и периодом
![]() .
.
Не
следует путать циклическую частоту
![]() и
частоту колебаний
и
частоту колебаний
![]() .
Между ними простая связь. Так как
.
Между ними простая связь. Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
.
Величина
![]() называется
фазой колебания. При t=0 фаза равна
называется
фазой колебания. При t=0 фаза равна
![]() ,
потому
называют
начальной фазой.
,
потому
называют
начальной фазой.
Отметим, что при одном и том же t:
![]()
где
![]() -
начальная фаза .Видно, что начальная
фаза для одного и того же колебания
есть величина, определенная с точнотью
до
-
начальная фаза .Видно, что начальная
фаза для одного и того же колебания
есть величина, определенная с точнотью
до
![]()
Закон
Ома (10.7)
|
Второй
закон Ньютона (4.6)
|
Уравнение
динамики вращательного движения
(7.3)
|
|
||
|
|
|
Используя другое обозначение производной получим после несложных преобразований: |
||
|
|
|
Мы получили дифференциальные уравнения, описывающие движения наших систем. В первых двух случаях уравнения одинаковы по форме, в третьем случае второй член уравнения содержит не φ, а Sin φ .
3)Пружинный и математический маятники.
*Пружинный маятник
На груз m горизонтального пружинного маятника действуют сила тяжести (m⋅g), сила реакции опоры (N) и сила упругости пружины (Fynp) (рис. 3, первый две силы на рис. а не указаны). Запишем второй закон Ньютона для случая, изображенного на рис. 3, б
![]()
0Х: ![]() или
или ![]()
а (материал с сайта science.up-life.ru)
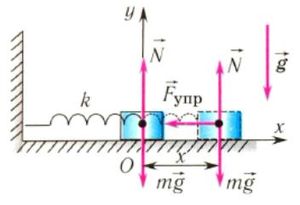
б
Рис. 3.
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора
![]()
Сравнивая полученное выражение с уравнением гармонических колебаний
![]()
находим циклическую частоту колебаний пружинного маятника
![]()
Тогда период колебаний пружинного маятника будет равен:
![]()
*Математический маятник
На груз m математического маятника действуют сила тяжести (m⋅g) и сила упругости нити (Fynp) (сила натяжения) (рис. 4). Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для случая, изображенного на рис. 4, б
![]()
![]()
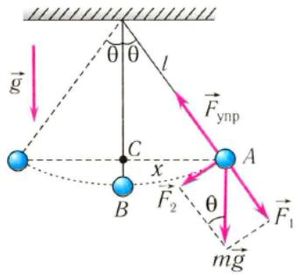
б
Рис. 4.
Пусть x — длина дуги AB, следовательно, x = l⋅θ, где угол θ выражен в радианах. Заметим, что при малых углах θ
![]()
Тогда
![]() или
или ![]()
Сравнивая полученное выражение с уравнением гармонических колебаний
находим, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
![]()
Тогда период колебаний маятника будет равен:
![]()
5)Незатухающие электрические колебания. Энергия электрических колебаний.
Простейший колебательный контур. Формула Томсона
В простейшем случае, когда омическое сопротивление равно нулю (R = 0) и источник э.д.с. отсутствует (E = 0), колебательный контур состоит лишь из конденсатора C и катушки индуктивности L и описывается дифференциальным уравнением
![]()
В таком контуре будут происходить незатухающие электрические колебания с периодом
![]()
Данная формула называется формулой Томсона в честь английского физика Уильяма Томсона (1824-1907), который теоретически вывел ее в 1853 году.
В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.
![]()
![]()
6)Графическое представление колебаний.
Период
гармонических колебаний равен:
T = 2π/![]() .
Число
колебаний в единицу времени
называется частотой
колебаний ν.
Частота
гармонических колебаний равна:
ν = 1/T. Единица измерения частоты герц (Гц)
- одно колебание в секунду.
Круговая
частота
=
2π/T = 2πν дает число колебаний за 2π
секунд.
.
Число
колебаний в единицу времени
называется частотой
колебаний ν.
Частота
гармонических колебаний равна:
ν = 1/T. Единица измерения частоты герц (Гц)
- одно колебание в секунду.
Круговая
частота
=
2π/T = 2πν дает число колебаний за 2π
секунд.
Графически гармонические колебания можно изображать в виде зависимости x от t (рис.1.1.А), так и методом вращающейся амплитуды (метод векторных диаграмм)(рис.1.1.Б).
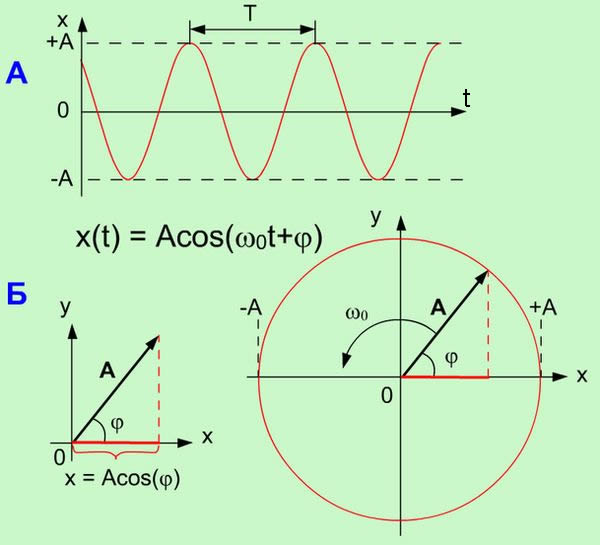
Метод
вращающейся амплитуды позволяет
наглядно представить все параметры,
входящие в уравнение гармонических
колебаний. Действительно, если вектор
амплитуды Арасположен
под углом φ к оси х (см. Рисунок
1.1. Б), то его проекция на ось х будет
равна: x = Acos(φ). Угол φ и есть начальная
фаза. Если вектор А привести
во вращение с угловой скоростью
,
равной круговой частоте колебаний, то
проекция конца вектора будет перемещаться
по оси х и принимать значения, лежащие
в пределах от -A до +A, причем координата
этой проекции будет меняться со временем
по закону:
![]() .
Таким
образом, длина вектора равна амплитуде
гармонического колебания, направление
вектора в начальный момент образует с
осью x угол равный начальной фазе
колебаний φ, а изменение угла
направления от времени равно фазе
гармонических колебаний. Время, за
которое вектор амплитуды делает один
полный оборот, равно периоду Т
гармонических колебаний. Число оборотов
вектора в секунду равно частоте колебаний
ν.
.
Таким
образом, длина вектора равна амплитуде
гармонического колебания, направление
вектора в начальный момент образует с
осью x угол равный начальной фазе
колебаний φ, а изменение угла
направления от времени равно фазе
гармонических колебаний. Время, за
которое вектор амплитуды делает один
полный оборот, равно периоду Т
гармонических колебаний. Число оборотов
вектора в секунду равно частоте колебаний
ν.
7)Собственные затухающие колебания. Параметры затухающих колебаний.
Собственные затухающие колебания происходят в колебательном контуре RLC(рис. 11.1. и 11.5.).
Рис. 11.5.
Эти колебания можно описать следующим дифференциальным уравнением (правило напряжений Кирхгофа):
IR – UC = eСИ. (11.6)
Здесь
по-прежнему: I = ![]() ; UC =
; UC = ![]() ;
eСИ =
;
eСИ = ![]() =
= ![]() =
= ![]() .
.
Учитывая эти соотношения, уравнению (11.6) придадим следующий вид:
![]() ;
;
![]() . (11.7)
. (11.7)
Здесь
d = ![]() —
коэффициент затухания;
—
коэффициент затухания; ![]() =
= ![]() —
частота собственных незатухающих
колебаний.
—
частота собственных незатухающих
колебаний.
Уравнение (11.7) — дифференциальное уравнение собственных затухающих электрических колебаний.
Если
в системе ![]() ,
то решением этого уравнения является
следующая функция:
,
то решением этого уравнения является
следующая функция:
q = Ae–dtcos(wt + j). (11.8)
Здесь А и j — постоянные, которые можно найти, воспользовавшись начальными условиями, а частота колебаний:
![]() . (11.9)
. (11.9)



