
- •1. Пересечение множеств. Законы пересечения множеств.
- •2. Объединение множеств. Законы объединения множеств.
- •Переместительный (коммутативный)
- •3. Дистрибутивные (распределительные) законы, связывающие объединение и пересечение множеств.
- •4. Вычитание множеств. Понятие дополнения подмножества.
- •5. Понятие разбиения множества на попарно-непересекающиеся подмножества или классы.
- •Разбиение при помощи 1-го свойства
- •Разбиение при помощи 2-х свойств
- •Разбиение при помощи 3-х свойств
- •6. Декартово произведение множеств. Изображение декартова произведения двух числовых множеств на координатной плоскости.
- •7. Особенности математических понятий. Объем и содержание понятия. Определение понятий. Структура определения понятия через род и видовое отличие.
- •8. Понятие высказывания Смысл слов "и", "или" в
- •9. Правила построения отрицания высказываний различной
- •10. Понятие высказывательной формы (предиката).
- •11. Отношения логического следования и равносильности
- •12. Неполная индукция. Простейшие схемы дедуктивных
- •13. Понятие бинарного отношения между элементами
- •14. Отношение эквивалентности и его связь с разбиением множества на попарно-непересекающиеся подмножества или классы.
- •15. Отношение порядка, его виды.
- •16. Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному.
- •17. Взаимно-однозначные соответствия. Равномощные множества.
- •18. Определение числовой функции. Способы задания функции. Прямая пропорциональность, ее свойства и график.
- •19. Определение числовой функции. Способы задания функции. Обратная пропорциональность, ее свойства и график.
- •Обратная пропорциональность
- •20. Понятие числового выражения, числового равенства и неравенства. Основные свойства истинных числовых равенств и неравенств.
- •21. Понятие уравнения с одной переменной. Равносильные уравнения. Теоремы о равносильности уравнений.
- •22. Понятие отношения делимости. Делимость суммы, разности и произведения целых неотрицательных чисел.
- •23. Признаки делимости на числа 2, 3, 4, 5, 9 и 25 в десятичной системе счисления.
- •24. Наибольший общий делитель и наименьшее общее кратное (на примерах)
1. Пересечение множеств. Законы пересечения множеств.
ПЕРЕСЕЧЕНИЕМ МНОЖЕСТВ A и B называется множество всех тех и только тех элементов, которые одновременно принадлежат множеству A и множеству B.
Рассмотрим различные случаи:
1
 )
)
A B = Ø
2 ) A B
C A B = C
3
 )
B
)
B
A Ϲ B = A
A
4 )
A = B A A = A
5) A Ø = Ø
Для операции пересечения выполняются следующие законы:
1 . Переместительный (коммутативный)
A B = B A
Пересечение мн-в A и B равно пересечению мн-в B и A.
2 . Сочитательный (ассоциативный)
(A B) C = A (B C)
Пересечение пересечения мн-в A и B и мн-ва С равно пересечению мн-ва A и пересечения мн-в B и C.
2. Объединение множеств. Законы объединения множеств.
Объединением множеств A и B называется множество всех элементов, которые принадлежат множеству A или множеству B.
Рассмотрим различные случаи:
 A
B
A
B
1) A U B
 A B
A U B = x
A B
A U B = x
2) x
3
 )
B A U B = B
)
B A U B = B
A

A U A = A
4) A=B
5) A U Ø = A
Для операции объединение выполняются следующие законы:
Переместительный (коммутативный)
A U B = B U A
Сочетательный (ассоциативный)
(A U B) U C = A U (B U C) (Объединение объединения множеств A и B и множества C равно объединению множества A и объединения множеств B и C)
3. Дистрибутивные (распределительные) законы, связывающие объединение и пересечение множеств.
Взаимосвязь пересечения и объединения мн-в отражается в распределительных, или дистрибутивных, свойствах этих операций. Таких св-в 2:
1) Пересечение дистрибутивно относительно объединения мн-в, т.е. для любых мн-в A, B и C выполняется равенство
( A
U
B)
C
= (A
C)
U
(B
C).
A
U
B)
C
= (A
C)
U
(B
C).
пересечение объединения множеств А и В и множества С равно объединению пересечений множеств А и С
2) Объединение дистрибутивно относительно пересечения мн-в, т.е. для любых мн-в A, B и C выполн. равенство
(A B) U C = (A U C) (B U C)
объединение пересечения множеств А и В и множества С равно пересечению объединений множеств А и С и множеств В и С.
Пример:
А = (-3; 8] AUB = (3; 9)
B = [0; 9) А В = [0; 8]
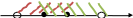
-3 0 8 9 Х
4. Вычитание множеств. Понятие дополнения подмножества.
РАЗНОСТЬЮ МН-В A и B называется мн-во всех элементов, принадлежащих мн-ву A и не принадлежащих мн-ву B.
A
 \ B = A 1) A B
\ B = A 1) A B
2

 )
A B
)
A B
B Ϲ A 3) A
A
B
\ B = B’A
Если B – подмн-во A, то разность мн-в A и B называется дополнением мн-ва B до мн-ва A.
 A
A
B U B’A =
B B’A = Ø

4) A \ A = Ø
A = B
5) A \ Ø = A
