4.11. Составить эмм и решить транспортную задачу.

В трех хранилищах горючего ежедневно хранятся 175, 125 и 140т бензина. Этот бензин ежедневно получает четыре заправочные станции в количествах равных соответственно 180, 110, 60 и 40т. Тарифы перевозок 1т бензина с хранилищ к заправочным станциям задаются матрицей:

9 7 5 3

С= 1 2 4 6

8 10 12 1

Составить такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.

Математическая модель транспортной задачи:

F = ∑∑c_ijx_ij, (1)

при условиях:

∑x_ij = a_i, i = 1,2,…, m, (2)

∑x_ij = b_j, j = 1,2,…, n, (3)

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

	1	2	3	4	Запасы
1	9	7	5	3	175
2	1	2	4	6	125
3	8	10	12	1	140
Потребности	180	110	60	40

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 175 + 125 + 140 = 440

∑b = 180 + 110 + 60 + 40 = 390

Занесем исходные данные в распределительную таблицу.

	1	2	3	4	5	Запасы
1	9	7	5	3	0	175
2	1	2	4	6	0	125
3	8	10	12	1	0	140
Потребности	180	110	60	40	50

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	1	2	3	4	5	Запасы
1	9	7[110]	5[60]	3	0[5]	175
2	1[125]	2	4	6	0	125
3	8[55]	10	12	1[40]	0[45]	140
Потребности	180	110	60	40	50

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

	v1=8	v2=7	v3=5	v4=1	v5=0
u1=0	9	7[110]	5[60]	3	0[5]
u2=-7	1[125]	2	4	6	0
u3=0	8[55]	10	12	1[40]	0[45]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij.

Минимальные затраты составят:

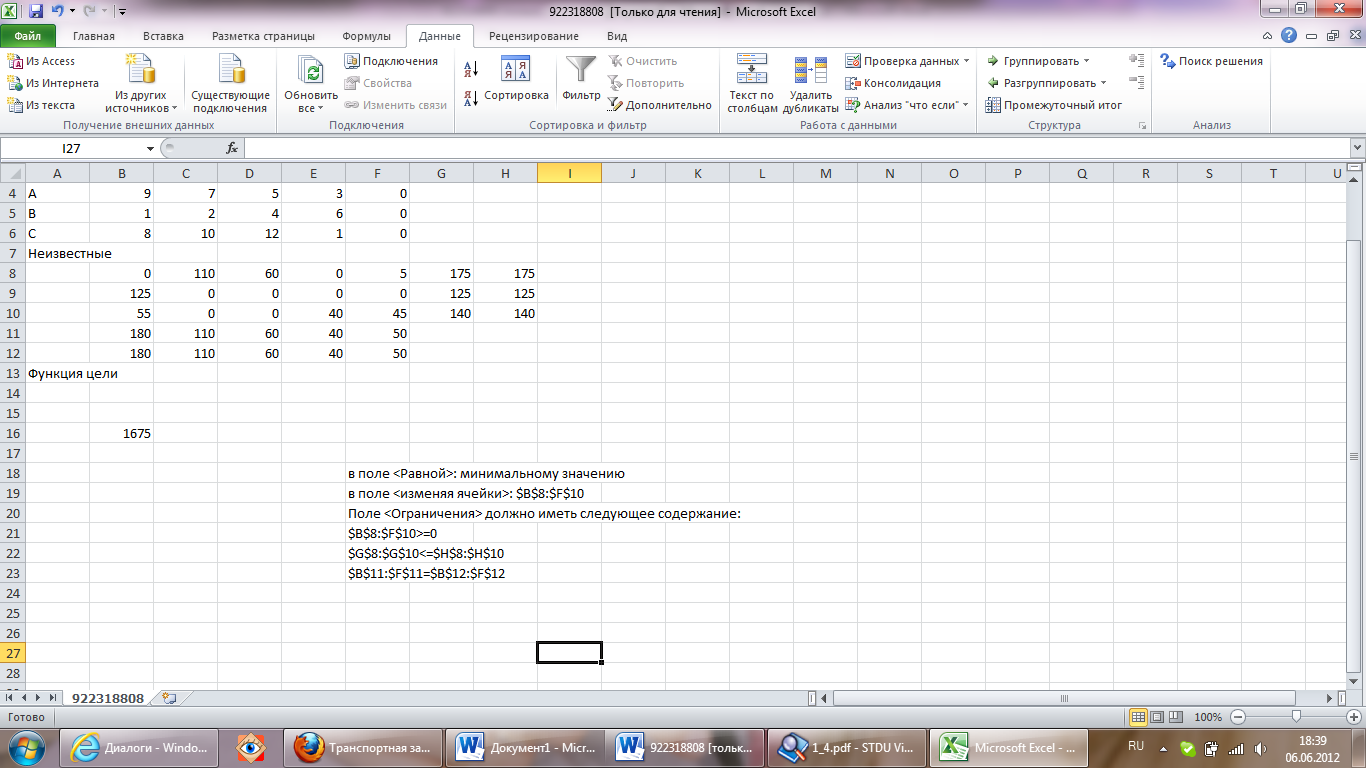
F(x) = 7*110 + 5*60 + 0*5 + 1*125 + 8*55 + 1*40 + 0*45 = 1675

РЕШЕНИЕ В EXCEL:

5.11. Большой универсальный магазин планирует заказать новую коллекцию для весеннего сезона. Решено заказать 4 вида костюмов. Три вида это костюмы отечественного производства: однобортные, двубортные, китель, и дорогие импортные костюмы. Затраты и прибыль от продажи костюмов представлена в таблице:

Вид костюма	Прибыль на 1 костюм, руб	Рабочее время продавцов, чел, -ч	Затраты на рекламу, руб	Торговая площадь на 1 костюм, м2
Однобортные	35	0,4	2	1,0
Двубортные	47	0,5	4	1,5
Китель	30	0,3	3	1,25
Импортные	90	1,0	9	3,0

Весенний сезон длится 90 дней. Магазин открыт 10ч в день, 7 дней в неделю. В отделе постоянно работают 2 продавца. Площадь отдела 600 м2. На рекламу выделено 15000 руб.

Сколько костюмов каждого вида надо закупить для получения максимальной прибыли. Если владелец магазина считает необходимым закупить не менее 200 костюмов каждого вида, то, как это отразится на прибыли ? изменится ли оптимальное решение, если прибыль от продажи однобортного костюма переоценена (недооценена) на 2(4) рубля?

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Определим максимальное значение целевой функции

F(X) = 35x₁+47x₂+30x₃+90x₄

при следующих условиях-ограничений.

2x₁+4x₂+3x₃+9x₄≤150000

x₁+1.5x₂+1.25x₃+3x₄≤600

0.8x₁+x₂+0.6x₃+2x₄≤900

2x₁ + 4x₂ + 3x₃ + 9x₄ + 1x₅ + 0x₆ + 0x₇ = 150000

1x₁ + 1.5x₂ + 1.25x₃ + 3x₄ + 0x₅ + 1x₆ + 0x₇ = 600

0.8x₁ + 1x₂ + 0.6x₃ + 2x₄ + 0x₅ + 0x₆ + 1x₇ = 900

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

2	4	3	9	1	0	0
1	1.5	1.25	3	0	1	0
0.8	1	0.6	2	0	0	1

Решим систему уравнений относительно базисных переменных:

x₅, x₆, x₇,

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,0,0,150000,600,900)

Базис	В	x1	x2	x3	x4	x5	x6	x7
x5	150000	2	4	3	9	1	0	0
x6	600	1	1.5	1.25	3	0	1	0
x7	900	0.8	1	0.6	2	0	0	1
F(X0)	0	-35	-47	-30	-90	0	0	0

Переходим к основному алгоритму симплекс-метода.

Итерация №0.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В индексной строке F(x) выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₄, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i4

и из них выберем наименьшее:

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.

Базис	В	x1	x2	x3	x4	x5	x6	x7	min
x5	150000	2	4	3	9	1	0	0	16666.67
x6	600	1	1.5	1.25	3	0	1	0	200
x7	900	0.8	1	0.6	2	0	0	1	450
F(X1)	0	-35	-47	-30	-90	0	0	0	0

После преобразований получаем новую таблицу:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x5	148200	-1	-0.5	-0.75	0	1	-3	0
x4	200	0.33	0.5	0.42	1	0	0.33	0
x7	500	0.13	0	-0.23	0	0	-0.67	1
F(X1)	18000	-5	-2	7.5	0	0	30	0

Итерация №1.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В индексной строке F(x) выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее:

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (0.33) и находится на пересечении ведущего столбца и ведущей строки.

Базис	В	x1	x2	x3	x4	x5	x6	x7	min
x5	148200	-1	-0.5	-0.75	0	1	-3	0	-
x4	200	0.33	0.5	0.42	1	0	0.33	0	600
x7	500	0.13	0	-0.23	0	0	-0.67	1	3750
F(X2)	18000	-5	-2	7.5	0	0	30	0	0

Окончательный вариант симплекс-таблицы:

Базис	В	x1	x2	x3	x4	x5	x6	x7
x5	148800	0	1	0.5	3	1	-2	0
x1	600	1	1.5	1.25	3	0	1	0
x7	420	0	-0.2	-0.4	-0.4	0	-0.8	1
F(X3)	21000	0	5.5	13.75	15	0	35	0

Оптимальный план можно записать так:

x₅ = 148800

x₁ = 600

x₇ = 420

F(X) = 35*600 = 21000

Составим двойственную задачу к прямой задаче.

2y₁+y₂+0.8y₃≥35

4y₁+1.5y₂+y₃≥47

3y₁+1.25y₂+0.6y₃≥30

9y₁+3y₂+2y₃≥90

150000y₁+600y₂+900y₃ → min

y₁ ≥ 0

y₂ ≥ 0

y₃ ≥ 0

Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.

Из первой теоремы двойственности следует, что Y = C*A^-1.

Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Определив обратную матрицу D = А^-1 через алгебраические дополнения, получим:

Тогда Y = C*A^-1 =

Оптимальный план двойственной задачи равен:

y₁ = 0

y₂ = 35

y₃ = 0

Z(Y) = 150000*0+600*35+900*0 = 21000