
- •32Вопрос. Методы проверки выборки на нормальность.
- •33Вопрос. Критерий Стьюдента.
- •Б) случай связанных (парных) выборок
- •34Вопрос. Критерий Фишера.
- •35Вопрос. Критерий знаков (g-критерий).
- •36Вопрос. Критерий хи-квадрат.
- •37Вопрос. Критерий Колмогорова.
- •38Вопрос. Корреляционный анализ.
- •39Вопрос. Коэффициент корреляции Пирсона.
- •40Вопрос. Коэффициент корреляции Спирмена.
- •41Вопрос. Регрессивный анализ.
- •42Вопрос. Дисперсионный анализ.
- •43Вопрос. Однофакторный дисперсионный анализ для несвязных выборок.
- •44Вопрос. Однофакторный дисперсионный анализ для зависимых выборок.
- •45Вопрос. Основные требования к статистическим пакетам общего назначения.
- •46Вопрос. Прикладные программы для обработки и анализа данных. Пакет statistica
- •Пакет stadia
38Вопрос. Корреляционный анализ.
Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию. Корреляционный анализ состоит в определении степени связи между двумя случайными величинами X и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (xi, yi) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин X и Y. Для оценки степени взаимосвязи величин X и Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки X и Y распределены по нормальному закону. Коэффициент корреляции — параметр, который характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле:

Коэффициент корреляции изменяется от
-1 (строгая обратная линейная зависимость)
до 1 (строгая прямая пропорциональная
зависимость). При значении 0 линейной
зависимости между двумя выборками нет.
Корреляционная связь —
это согласованное изменение двух
признаков, отражающее тот факт, что
изменчивость одного признака находится
в соответствии с изменчивостью другого.
Корреляционная зависимость
- это изменения,
которые вносят значения одного признака
в вероятность появления разных значений
другого признака. Задача корреляционного
анализа сводится к установлению
направления (положительное или
отрицательное) и формы (линейная,
нелинейная) связи между варьирующими
признаками, измерению ее тесноты, и,
наконец, к проверке уровня значимости
полученных коэффициентов корреляции.
Корреляционные связи
различаются по
форме, направлению и степени (силе).
 По
форме корреляционная
связь может быть прямолинейной или
криволинейной. Прямолинейной может
быть, например, связь между количеством
тренировок на тренажере и количеством
правильно решаемых задач в контрольной
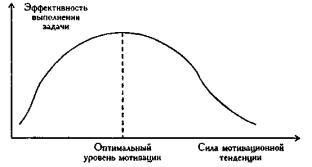
сессии. Криволинейной может быть,
например, связь между уровнем мотивации
и эффективностью выполнения задачи
(см. рис. 1). При повышении мотивации
эффективность выполнения задачи
сначала возрастает, затем достигается
оптимальный уровень мотивации, которому
соответствует максимальная эффективность
выполнения задачи; дальнейшему повышению
мотивации сопутствует уже снижение
эффективности. По
направлению корреляционная
связь может быть положительной
("прямой") и отрицательной
("обратной"). При положительной
прямолинейной корреляции более высоким
значениям одного признака соответствуют
более высокие значения другого, а более
низким значениям одного признака -
низкие значения другого. При отрицательной
корреляции соотношения обратные. При
положительной корреляции коэффициент
корреляции имеет положительный знак,
например r=+0,207,
при отрицательной корреляции -
отрицательный знак, например r=—0,207.
Степень, сила или
теснота корреляционной
связи определяется по величине
коэффициента корреляции. Сила связи не
зависит от ее направленности и определяется
по абсолютному значению коэффициента
корреляции. Максимальное возможное
абсолютное значение коэффициента
корреляции r=1,00;
минимальное r=0,00.
Общая классификация корреляционных
связей: сильная,
или тесная при
коэффициенте корреляции r>0,70;
По
форме корреляционная
связь может быть прямолинейной или
криволинейной. Прямолинейной может
быть, например, связь между количеством
тренировок на тренажере и количеством
правильно решаемых задач в контрольной
сессии. Криволинейной может быть,
например, связь между уровнем мотивации
и эффективностью выполнения задачи
(см. рис. 1). При повышении мотивации
эффективность выполнения задачи
сначала возрастает, затем достигается
оптимальный уровень мотивации, которому
соответствует максимальная эффективность
выполнения задачи; дальнейшему повышению
мотивации сопутствует уже снижение
эффективности. По
направлению корреляционная
связь может быть положительной
("прямой") и отрицательной
("обратной"). При положительной
прямолинейной корреляции более высоким
значениям одного признака соответствуют
более высокие значения другого, а более
низким значениям одного признака -
низкие значения другого. При отрицательной
корреляции соотношения обратные. При
положительной корреляции коэффициент
корреляции имеет положительный знак,
например r=+0,207,
при отрицательной корреляции -
отрицательный знак, например r=—0,207.
Степень, сила или
теснота корреляционной
связи определяется по величине
коэффициента корреляции. Сила связи не
зависит от ее направленности и определяется
по абсолютному значению коэффициента
корреляции. Максимальное возможное
абсолютное значение коэффициента
корреляции r=1,00;
минимальное r=0,00.
Общая классификация корреляционных
связей: сильная,
или тесная при
коэффициенте корреляции r>0,70;
средняя при 0,50<r<0,69;
умеренная при 0,30<r<0,49;
слабая при 0,20<r<0,29;
очень слабая при r<0,19.
