45. Определение параметров закона движения главного вала машинного агрегата.

Режимы движения механизмов

В зависимости от того какую работу совершают внешние силы машины различают три режима движения: разгон (разбег, пуск), торможение (выбег, останов) и установившееся движение (рис. 12.3).

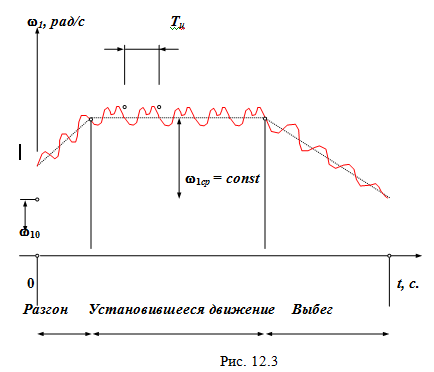
Установившимся движением механизма называют такое движение, при котором его обобщенная скорость и кинетическая энергия являются периодическими функциями времени. Минимальный промежуток в начале и в конце которого повторяются значения кинетической энергии и обобщенной скорости механизма – называют временем цикла установившегося движения.

Для идеальной механической системы, в которой нет потерь энергии и звенья абсолютно жесткие при получении уравнений движения механизма можно воспользоваться теоремой об изменении кинетический энергии: разность энергии за какой либо промежуток времени равна работе сил за тот же промежуток времени. ,где А_д.с. – работа движущих сил; А_п.с. – работа сил производственных сопротивлений; А_в.с. – работа сил вредных сопротивлений (трения и внешней среды); А_G – работа сил веса.

Для режима разгона: _i0 = 0, А_п.с. = 0, тогда: .

Работа движущих сил при разгоне расходуется кинетическую энергию, работу сил вредных сопротивлений и веса.

При установившемся движении за каждый цикл движения работа всех внешних сил равна нулю .

Для режима выбега: _i = 0, А_д.с. = 0, А_п.с. = 0 тогда: .

Запасённая кинетическая энергия при выбеге тратится на преодоление работ сил вредных сопротивлений и веса.

Режимы разгона и выбега называют режимами неустановившегося движения.

Уравнение движения механизма в дифференциальном виде

Содержит вторые производные от координат по времени. Изменение кинетической энергии механизма равно приращению работ сил действующих на механизм:

.

В случае если начальное звено совершает вращательное движение: .

Тогда: , ,

Преобразуем второе слагаемое с учетом: .

Подставляя получаем: .

В случае если J_пр = const (маховое колесо, ротор двигателя и т.п.) получаем (второй закон Ньютона для вращательного движения).

46. Учёт сил инерции звеньев машин.

Силы инерции звеньев

Силы инерции звеньев рассматриваются как реакции звена на изменение его скорости по величине и направлению. Существование сил инерции обусловлено двумя обстоятельствами: фактом наличия у звеньев массы и фактом движения звеньев, сопровождающегося в общем случае ускорениями отдельных точек и всего звена в целом, так как известно из теоретической механики, что мерой сил инерции является произведение массы на ускорение.

Из курса теоретической механики известно, что систему сил инерции в общем случае можно привести к силе – главному вектору сил инерции приложенного в центре масс s звена (рис. 11.6) и к паре сил, момент которой называется главным моментом сил инерции .

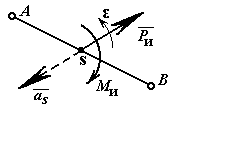
Рис. 11.6

Главный вектор сил инерции определяют по формуле: .

Главный момент сил инерции определяют по формуле: ,

где m – масса звена, кг; а_s – ускорение цента масс, м/с²; J_s – момент инерции звена относительно оси проходящей через центр масс перпендикулярной плоскости движения, кг/м²;  - угловое ускорение звена, с^-2.

Знак «» указывает на то, что векторы и соответственно направлены противоположно а_s и .