
- •1. Требования к машинам. Задачи курса Тмм и м.
- •2. Задачи проектирования машин. Критерии и стадии проектирования в ескд. Содержание технического предложения.
- •3. Машины и их классификация.
- •4. Основные сведения из теории производительности машин.
- •5. Машинный агрегат. Общее устройство.
- •6. Назначение, устройство и основные виды механизмов.
- •7. Строение механизмов. Кинематические пары. Подвижность кинематических пар и механизмов.
- •8. Стадии движения машинного агрегата. Установившееся движение. Энергетические соотношения при установившемся движении машин. Цикловой кпд.
- •Вопрос 9
- •Вопрос 10
- •Вопрос 11
- •Вопрос 12
- •Вопрос 13 (с. 69-72)
- •Вопрос 14 (с.68)
- •Вопрос 15
- •Вопрос 16 (с.37-41)
- •25. Условие соседства в эпициклическом механизме.
- •26. Условия сборки в эпициклическом механизме.
- •27. Основы синтеза планетарных передач по методу сомножителей.
- •28. Управление машинами-автоматами с помощью механизмов. Виды кулачковых механизмов.
- •Классификация кулачковых механизмов
- •30. Параметры закона движения кулачкового механизма.
- •34.Угол давления и его связь с основными размерами кулачкового мех-ма.
- •35.Учет угла давления при синтезе кулачкового механизма с поступательным и вращательным движением толкателя.
- •36.Профилирование кулачка по методу обращения движения.
- •37.Обобщённая инертность машинного агрегата.
- •38.Вычисление передаточной функции методами планов и диаграмм.
- •39.Вычисление передаточной функции аналитич. Методом.
- •40.Исследование движения машинного агрегата с помощью диаграммы энергомасс.
- •41. Постановка задачи о регулировании движения машинного агрегата.
- •42. Назначение маховика и определение его момента инерции.
- •44. Цель, теоретические основы и порядок силового исследования машин. Статически определимые кинематические цепи.
- •45. Определение параметров закона движения главного вала машинного агрегата.
- •46. Учёт сил инерции звеньев машин.
- •47. Порядок уточнения кпд машины и интенсивность износа кинематических пар.
- •48. Уравновешивание вращающихся масс (роторов)
- •49. Полное статическое уравновешивание рычажных механизмов.
34.Угол давления и его связь с основными размерами кулачкового мех-ма.
Угол давления – угол между вектором линейной скорости выходного звена (толкателя) и реакцией, действующей с ведущего звена (кулачка) на выходное звено. Эта реакция без учета сил трения направлена по общей нормали к взаимодействующим поверхностям. Угол давления определяется экспериментально. Для кулачкового механизма с поступательно движущимся толкателем допустимый угол давления равен: [θ] = 25º÷35º.
Для кулачкового механизма с качающимся толкателем допустимый угол давления равен: [θ] = 35º÷40º.
Реакцию
можно разложить на две составляющие:
![]() и
и
![]() .
.
Если, в силу каких‑либо причин, угол давления будет увеличиваться, то будет уменьшаться, а – увеличиваться.
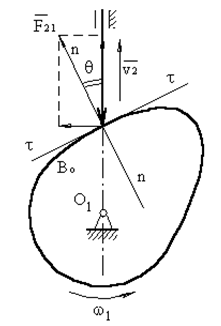
При достижении углов больше допустимого, возможен перекос оси толкателя в направляющей.
Реакцию можно разложить на две составляющие: и .
Если, в силу каких‑либо причин, угол давления будет увеличиваться, то будет уменьшаться, а – увеличиваться.
При достижении углов больше допустимого, возможен перекос оси толкателя в направляющей.
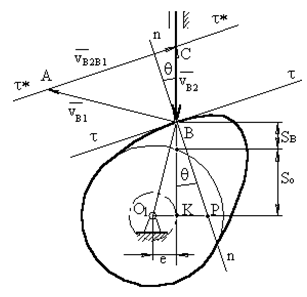
6.4.1 Вывод формулы для определения угла давления в кулачковом механизме.
Из
треугольника ΔКВР:
![]() (1)
, КР = О1Р
– О1К
= О1
– е
, КВ = so
+ sB
(1)
, КР = О1Р
– О1К
= О1
– е
, КВ = so
+ sB
![]() (2)
(2)
Треугольник
ΔО1ВР
подобен треугольнику ΔАВС.
Тогда
![]()
![]() vB1=
ω1·O1B
vB1=
ω1·O1B
![]()
Подставим
это выражение в (2):![]()
Знак “ – ” – для правой внеосности;
знак “ + ” – для левой внеосности.
Угол давления в кулачковом механизме зависит от размеров кулачковой шайбы: чем она больше, тем угол давления меньше.
35.Учет угла давления при синтезе кулачкового механизма с поступательным и вращательным движением толкателя.
Задача
динамического синтеза заключается в
нахождении центра вращения кулачка,
при условии минимизации размеров
механизма, когда заданы: закон движения
толкателя и предельно допустимый угол
давления
![]() .
В конечном итоге задача состоит в
определении rmin
кулачка,
после чего может быть решена задача
кинематического синтеза (профилирование).
.
В конечном итоге задача состоит в
определении rmin
кулачка,
после чего может быть решена задача
кинематического синтеза (профилирование).
Рассмотрим
пример определения rmin
кулачка для механизма с поступательно
движущимся толкателем, когда заданы
диаграммы перемещений S(φ)
и аналогов скоростей dS/dφ(φ),
которые должны быть вычерчены в едином
масштабе
Путём исключения параметра φ вычерчивается совмещённая диаграмма S(dS/dφ), как показано на рис. 57.
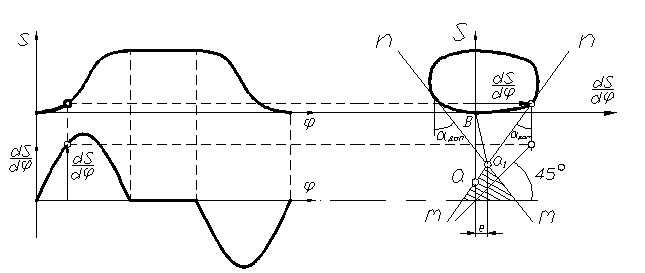 рис.
57
рис.
57
Проведя
касательные mn
к диаграмме S(dS/dφ)
под углами
,
как показано на рис. 57, получим точку
![]() на
их пересечении. Тогда отрезок
на
их пересечении. Тогда отрезок
![]() будет
соответствовать в масштабе
будет
соответствовать в масштабе
![]() величине
величине
![]() для
внеосного механизма со смещением оси
толкателя е≠0
относительно центра вращения кулачка.
Так как центр кулачка можно располагать
в любой точке заштрихованной области,
то при е=0
получим
для
внеосного механизма со смещением оси
толкателя е≠0
относительно центра вращения кулачка.
Так как центр кулачка можно располагать
в любой точке заштрихованной области,
то при е=0
получим
![]() ,
когда центр кулачка совпадает с осью
толкателя. Таким образом, габариты
механизма уменьшаются при
е≠0, т. к.
центр кулачка приближается к точке в,
а предельный угол давления
остаётся
неизменным.
,
когда центр кулачка совпадает с осью
толкателя. Таким образом, габариты
механизма уменьшаются при
е≠0, т. к.
центр кулачка приближается к точке в,
а предельный угол давления
остаётся
неизменным.
Обычно при силовом замыкании такие построения делаются только для фазы удаления, т. к. на фазе возврата толкатель является ведущим звеном и заклинивания не происходит.
Для
механизма с коромысловым толкателем
построение совмещённой диаграммы
S(dS/dφ)
производится в пределах заданного
максимального угла размаха коромысла
Ψmax.
Причём отрезки, равные dS/dφ
откладываются в масштабе
![]() от
траектории точки А коромысла по его оси
в сторону вектора dS/dφ,
повёрнутого на 90º в направлении вращения
кулачка (рис. 58).
от
траектории точки А коромысла по его оси
в сторону вектора dS/dφ,
повёрнутого на 90º в направлении вращения
кулачка (рис. 58).
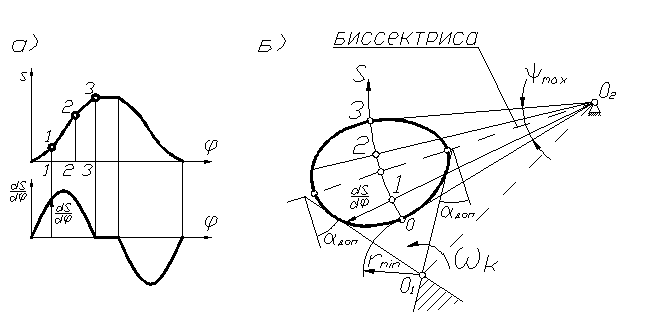 рис.
58
рис.
58
Точки,
полученные для нескольких положений
коромысла, соединяют плавной кривой и
строят допускаемую зону размещения
центра вращения кулачка, которую
приближённо можно получить, проведя
касательные к диаграмме S(dS/dφ)
под углами
,
образованными биссектрисой угла Ψmax
и перпендикулярами к ней (см. рис. 58, б).
Выбранное положение центра О1
в допускаемой (заштрихованной) зоне
определяет величину
![]() и
межцентровое расстояние О1О2
между кулачком и коромыслом.
и
межцентровое расстояние О1О2
между кулачком и коромыслом.
