3.2Интегрирование уравнений методом Эйлера

Пусть задано уравнение на с начальными условиями . Разделим отрезок точками , , ,… , на равных частей . Обозначим

, .

Пусть приближенное решение уравнения, в котором , , …, .

Обозначим , , … . В каждой точке , , … заменим производную отношением конечных разностей

, .

При

, , , ;

при

, ,

;

при

, ,

;

…

при

, ,

;

…

при

, ,

.

Соединяя на координатной плоскости точки , , … отрезками прямой, получим ломаную линию Эйлера. Известно доказательство [ 5 ] следующего утверждения: если существует единственное решение , удовлетворяющее начальным условиям на , то

, .

Для повышения точности интегрирования, метод Эйлера используют совместно с формулой Тейлора (разложения функции в ряд). Этот прием называют методом Адамса [ 5 ].

В качестве примера рассмотрим решение интегро-дифференциального уравнения (методом Эйлера), составленного для последовательного колебательного контура Рис. А.

,

со следующими начальными условиями , , и правой частью, определяемой следующим выражением .

Продифференцируем левую и правую части уравнения и получим следующее уравнение

.

Перенесем коэффициент при старшей производной из левой части в правую часть и получим следующее уравнение

.

Представим уравнение в виде следующего разностного уравнения

.

Преобразуем разностное уравнение следующим образом

,

.

Выделим из уравнения состояние тока в момент времени зависящее от предыдущих состояний ,

.

Вычисления начинаются с начальными условиями , .

Процедура интегрирования уравнения , средствами пакета MathCad, представлена на Рис. 3..

Рис. 3.5 – MathCAD. Процедура интегрирования

Результат интегрирования, при значениях , , , , и входном сигнале , представлен на Рис. 3..

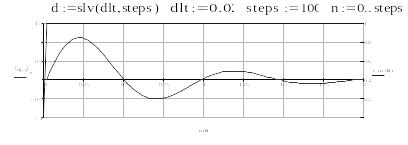
Рис. 3.6 – MathCAD. Результаты интегрирования

3.3Интегрирование уравнений методом Адамса

Пусть задано уравнение

на отрезке с начальными условиями , [ 11 ]. Разделим отрезок точками , , ,… , на равных частей .

Обозначим приближенные значения решения в точках

, , …

через

, , … .

Вычислим разности первого порядка по следующим формулам

,

,

...

.

Вычислим разности второго порядка по следующим формулам

,

,

...

.

Вычислим разности вторых разностей, разности третьих разностей и т. д. по тем же правилам.

Обозначим через , , … приближенные значения производных в точках , , … .

Обозначим через , , … приближенные значения вторых производных в этих точках и т. д.

Вычислим первые разности производных по формулам

,

,

...

.

Вычислим вторые разности производных по формулам

,

,

...

.

Последующие разности производных вычисляем по тем же правилам.

Напишем формулу Тейлора [ 10 ] для решения уравнения в окрестности точки

.

Значение этой формуле известно. Значения , ,… производных находим из уравнения , дифференцируя члены этого уравнения по .

вычисляем по формуле .

Далее, дифференцируя члены уравнения , и подставляя значения , , получим

.

Далее, дважды дифференцируя члены уравнения , и подставляя значения , , , , получим .

Выполняя такие действия, мы можем найти значения производных любого порядка при .

Таким образом, все члены кроме остаточного члена , известны. Пренебрегая остаточным членом, получим приближенное значение решения при любом значении . Точность вычисления зависит от величины и числа членов в разложении.

Используя формулу Тейлора, определим значения , при и по следующим формулам

Используя величины , , , определим

, , .

Используя величины , , , определим

, , .

Допустим, что нам известны значения решения , , ,… . На основании этих значений можно вычислить, используя уравнение , значения производных , , ,… , а следовательно

, , ,… , и

, , ,… .

Определим значение по формуле Тейлора, полагая

, ,

.

Ограничившись четырьмя членами разложения, получим

.

В этой формуле величины , неизвестны. Их определяют через известные разности первого и второго порядков.

Представим по формуле Тейлора , полагая , ,

.

и , полагая , ,

.

Из равенства найдем

.

Вычитая из членов равенства члены равенства , получим

.

Из и находим

,

или

.

Подставляя выражение в равенство , получим

Подставляя и в разложение , получим

Это выражение называют формулой Адамса с четырьмя членами. Формула дает возможность, зная , , определить . Таким образом, зная , , , возможно определить и далее , ...

Известно доказательство следующего утверждения. Если существует единственное решение уравнения на отрезке , то погрешность приближенных значений, определяемых по формуле , по абсолютной величине не превосходит , где ‑ постоянная, зависящая от длины интервала и вида функции и не зависящая от величины [ 10 ].

В том случае, когда необходима большая точность вычисления, то следует брать больше, чем в разложении , членов, и формула изменится. Если мы возьмем формулу, содержащую пять членов, то вместо формулы получим следующую формулу

.

В этой формуле определяется через значения , , и . Таким образом, чтобы начать вычисления по этой формуле, нужно знать четыре первых значения решения , , , .

Рассмотрим пример нахождения приближенных значений решения уравнения , удовлетворяющего начальному условию при .

Значения решения определим при , , , .

Сначала определим , по формулам , . Из уравнения и начальных данных получим значение для

.

Дифференцируя данное уравнение, получим . Значение для будет

.

Дифференцируя еще раз данное уравнение, получим . Значение для будет .

Подставляя в уравнение значения , , , и получим

.

При получим

.

Зная , , находим

,

,

,

,

,

.

По формуле находим значение

.

Далее находим значения , , и по формуле находим значение

.

Точное решение заданного уравнения определяется выражением .

Следовательно, .

Абсолютная погрешность вычислений, по методу Адамса, равна , а относительная погрешность равна .

Абсолютная погрешность вычислений, по методу Эйлера, равна , а относительная погрешность равна .