3Цифровая обработка сигнала
Входной
сигнал
преобразуется в дискретный с помощью
электронного ключа. Ключ работает с
шагом
.
Сигнал
на выходе ключа имеет вид последовательности
равностоящих во времени импульсов,
являющихся выборками (или отсчетами)
сигнала
.
Каждый отсчет обрабатывается аналого-цифровым преобразователем (АЦП) за время, меньшее чем . Отсчет квантуется по уровню и преобразуется в кодовое слово, состоящее из n разрядов.
Цифровой фильтр, представляющий собой некоторое вычислительное устройство, обрабатывает входные кодовые слова определенными математическими операциями (например, сложение, умножение, задержка во времени) и вырабатывает выходные слова.
В цифро-аналоговом преобразователе (ЦАП) кодовые слова, поступающие от цифрового фильтра (ЦФ), преобразуется в аналоговые отсчеты.
В
сглаживающем фильтре (СФ) дискретные
последовательности (аналоговые отсчеты)
преобразуются в континуальный выходной
сигнал
.
Функциональная схема цифрового фильтра
представлена на Рис. 3..
Рис. 3.1 – Функциональная схема цифрового фильтра
Дискретный
сигнал на входе ЦФ представляет собой
последовательность из N
отсчетов
,
,
взятых с интервалом
из континуального сигнала
.
На
выходе фильтра возникает последовательность
чисел
.
Выходная последовательность состоит
из N отсчетов,
,
взятых с интервалом
.
3.1Структура цифровых ких и бих фильтров
Алгоритм
ЦФ вырабатывает выходной сигнал
в момент времени
,
зависящий только от числа
и предшествующих ему входных чисел
,
где:
- весовые коэффициенты (действительные постоянные числа);
-
максимальное число запоминаемых чисел.
Начиная
с момента
выходные числа фильтра, в моменты
,
,
,
будут определяться выражением
;
;
;
.
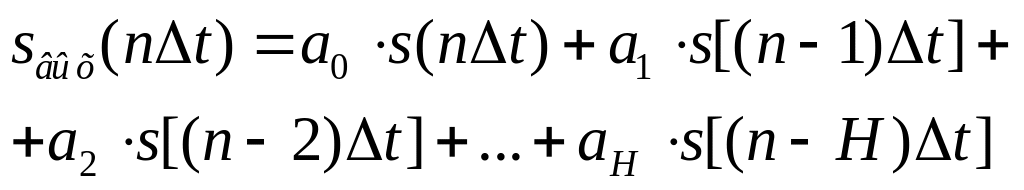Приведенные соотношения можно записать
,
где
- называют элементом памяти или элементом задержки (интервал поступления отсчетов сигнала). Структура цифрового фильтра представлена на Рис. 3..
При
подаче на вход фильтра сигнала
на выходе фильтра возникает
последовательность, которую называют
импульсной характеристикой фильтра
.
Для структуры, представленной на Рис. 3.
числа
совпадают с весовыми коэффициентами
.
Импульсная характеристика этого цифрового фильтра представлена на Рис. 3..
р ло рглпрггпьонпттнроаеншекмаиевнукм5уек
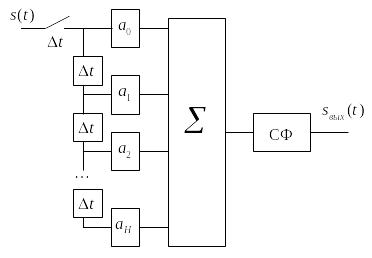
Рис. 3.2 – Структура цифрового КИХ фильтра
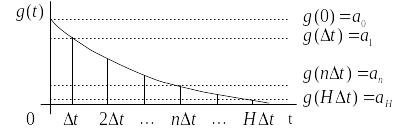
Рис. 3.3 – Импульсная характеристика цифрового фильтра
Дискретный эквивалент интегральной свертки выглядит следующим образом
.
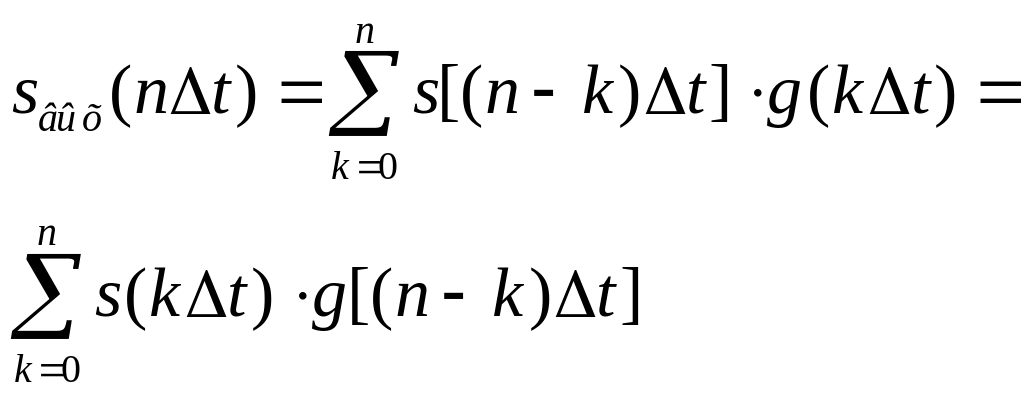Импульсная
характеристика фильтра
может быть получена из импульсной
характеристики соответствующего
аналогового фильтра путем дискретизации
с шагом
.
Сигналы на выходе СФ и аналогового
фильтра совпадают. Такой фильтр называют
трансверсальным или поперечным.
Если
ввести дополнительные обратные связи,
то сигнал на выходе сумматора в момент
времени
будет зависеть не только от
отсчетов входного сигнала, но и от
некоторого количества отсчетов выходного
сигнала в предыдущие моменты. Подобные
фильтры называют рекурсивными.
В
этом случае разностное уравнение
заменяется другим, более общим уравнением,
учитывающим обратные связи с весовыми
коэффициентами
Для первой реализации ЦФ импульсная характеристика содержит конечное число отсчетов (не более ). Для второй реализации ЦФ , число отсчетов может быть бесконечно. Структура этого фильтра представлена на Рис. 3. .
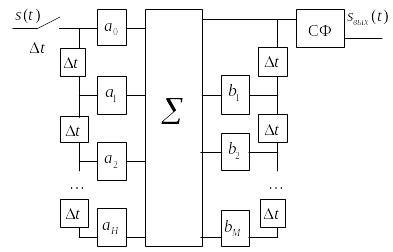
Рис. 3.4 – Структура цифрового БИХ фильтра
Трансверсальные фильтры называют КИХ-фильтрами. Рекурсивные фильтры называют БИХ-фильтрами [ 2 ].