2.3Фильтры второго порядка

Цепи, соответствующие передаточным функциям второго порядка, разделяют, по частотным характеристикам, на шесть следующих групп:

• цепи нижних частот;

• цепи верхних частот;

• полосно-пропускающие цепи;

• частотно заграждающие цепи;

• частотно-выделяющие цепи;

• всепропускающие цепи.

1. Фильтры нижних частот

Цепи нижних частот второго порядка описываются следующей передаточной функцией

,

где полюсы этой функции, .

Число представляет собой вещественную часть полюсов.

Размещение полюсов и ( , ) на комплексной плоскости, АЧХ и ФЧХ фильтра нижних частот второго прядка представлены на Рис. 2..

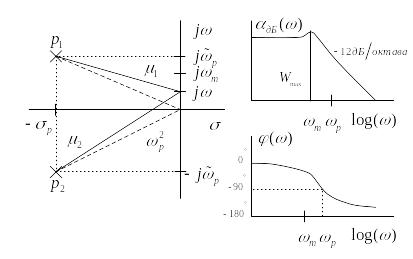
Рис. 2.5 – Фильтр нижних частот второго порядка

Амплитудно-частотная характеристика фильтра, на частоте , определяется следующим выражением

,

или

,

Найдем значение переменной , при котором функция принимает наибольшее значение. Так как числитель функции это постоянная величина, то функция принимает наибольшее значение , при знаменателе функции , принимающем наименьшее значение.

Подставим выражения в знаменатель

.

Функция, расположенная под корнем, это неотрицательная и немонотонная функция, имеющая перегибы. Раскроем скобки в этой функции и получим удобное, для нахождения производной, выражение

Упростим полученное выражение, группируя коэффициенты при переменных , , ,

.

Найдем производную (по переменной ) для этого выражение и приравняем производную нулю. Получим следующие уравнение

.

Решение этого уравнения даст точки перегиба. Уравнение станет равенством в двух следующих случаях: при и при .

Обозначим переменную как искомую переменную . При функция примет наибольшее значение . Очевидно, что .

Подставим выражение в и получим выражение для

.

Следует отметить, что при , а при .

2. Фильтры верхних частот

Цепи верхних частот второго порядка описываются следующей передаточной функцией

,

где полюсы и ноль этой функции, . Число представляет собой вещественную часть полюсов.

Размещение полюсов и ( , ) и нуля на комплексной плоскости, АЧХ и ФЧХ фильтра верхних частот второго прядка представлены на Рис. 2..

АЧХ фильтра определяется следующим выражением

,

Следует отметить, что частотные характеристики фильтра верхних частот второго порядка симметричны частотным характеристикам фильтра нижних частот второго порядка.

3. Полосно-пропускающие фильтры

Полосно-пропускающие цепи второго порядка описываются следующей передаточной функцией

,

где полюсы и ноль этой функции, . Число представляет собой вещественную часть полюсов.

Рис. 2.6 – Фильтр верхних частот второго порядка

Размещение двух полюсов и ( , ) и нуля на комплексной плоскости, АЧХ и ФЧХ полосно-пропускающего фильтра второго прядка представлены на Рис. 2..

АЧХ фильтра определяется следующим выражением

,

Для полосно-пропускающего фильтра второго порядка частота наибольшего значения АЧХ совпадает с частотой . Наибольшее значение АЧХ в этом случае равно коэффициенту .

Частотные характеристики фильтра симметричны относительно частоты . Граничные частоты и представляют собой границы по уровню 3 дБ, а полоса пропускания фильтра по уровню 3 дБ равна .

Рис. 2.7 – Полосно-пропускающий фильтр второго порядка