2Линейная фильтрация сигнала

Электрическим фильтром называют устройство, при помощи которого электрические колебания разных частот отделяют друг от друга [ 1, 2, 6 ]. Такое устройство представляют или как пассивный или как активный четырехполюсник, пропускающий некоторую, определенную полосу частот с малым затуханием.

Полосу частот, при которой затухание мало, называют полосой пропускания фильтра. Остальную область частот называют полосой задерживания фильтра.

2.1Классификация фильтров

Известны следующие способы классификации электрических фильтров:

а) В зависимости от пропускаемой полосы частот электрические фильтры разделяют на:

• фильтры нижних частот (низкочастотные);

• фильтры верхних частот (высокочастотные);

• полосовые фильтры;

• заграждающие фильтры (режекторные).

б) В зависимости от схем звеньев (Рис. 2.), образующих электрический фильтр, фильтры разделяют на:

• фильтры, состоящие из Г образных звеньев;

• фильтры, состоящие из Т образных звеньев;

• фильтры, состоящие из П образных звеньев;

• мостовые фильтры;

• однозвенные фильтры;

• многозвенные фильтры и др.

в) В зависимости от характеристических сопротивлений фильтры разделяют на:

• простейшие фильтры типа k;

• фильтры более высокого класса типа m и др.

г) В зависимости от типа используемых элементов фильтры разделяют на:

• реактивные фильтры (состоящие из L и C элементов);

• пьезоэлектрические фильтры (состоящие кварцевых пластин);

• безындукционные фильтры (состоящие из R и C элементов) и др.

Схемы фильтров, как правило, принадлежат к семейству конечных линейных цепей с сосредоточенными параметрами (сюда не входят нелинейные, распределенные и бесконечные цепи, и их сочетания).

Работу активного фильтра (фильтр содержит источник энергии и в большинстве случаев полное сопротивление источника сигнала равно нулю, а сопротивление нагрузки бесконечно) можно представить следующим образом см. Рис. 2..

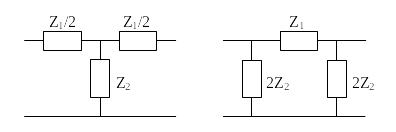
Рис. 2.1– Симметричные Т и П фильтры

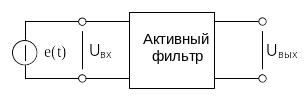
Рис. 2.2 – Подключение и работа активного фильтра

2.2Частотные характеристики фильтров

Выходной сигнал цепи n–го порядка можно определить через входной сигнал, линейным дифференциальным уравнением n–го порядка, имеющим следующий вид

,

где это входной сигнал, а это выходной сигнал и [ 4 ]. Применив к этому уравнению преобразование Лапласа, получим передаточную функцию фильтра в виде отношения двух полиномов и

,

где представляет собой комплексную частоту, а и являются полиномами переменной с вещественными коэффициентами и .

Записав полиномы и в виде сомножителей, получим полюсы и нули передаточной функции

.

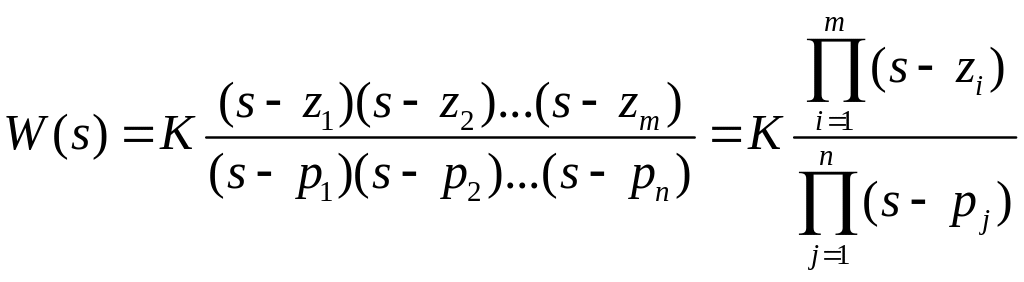Полюсы и нули могут быть либо вещественными, либо комплексно-сопряженными. В том случае, когда числитель передаточной функции представляет собой постоянное число, считают, что его нули функции находятся в бесконечности.

Пара комплексно сопряженных полюсов и нулей определяет передаточную функцию второго порядка

,

где и .

Полюсы и нули изображают на плоскости комплексной частоты или  - плоскости (Рис. 2.). Очевидно, что , , , .

Следует отметить, что вещественные части полюсов и нулей , отображают на комплексной плоскости для определения частотных характеристик фильтров, а величины , являются физически измеряемыми параметрами. Они отражают конструктивные особенности фильтров.

Для нахождения частотной характеристики цепи предполагают, что входной сигнал гармонический. Так как цепь линейна то выходной сигнал так же гармонический.

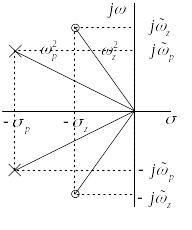
Рис. 2.3 – Полюсы и нули функции второго порядка

В этом случае осуществляют подстановку и получают

.

Логарифмируя частотную передаточную функцию, получим выражение

,

где и представляют АЧХ и ФЧХ (в неперах и градусах).

АЧХ в децибелах вычисляют по следующему правилу

.

Характеристика группового времени замедления определяется следующим выражением

.

АЧХ и ФЧХ передаточной функции можно получить графически, используя ее полюсы и нули.

Для любой частоты АЧХ и ФЧХ определяются из следующего выражения

.

Каждый сомножитель в этом уравнении представляет собой вектор на комплексной плоскости

,

.

АЧХ и ФЧХ, учитывая , , примут следующий вид

,

.

Рассмотрим, в качестве примера, следующую передаточную функцию

.

Нули и полюсы этой функции, расположенные на комплексной плоскости (Рис. 2.), определят амплитуду фазу выходного сигнала, на частоте , следующим образом

,

.

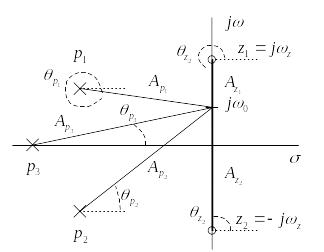
Рис. 2.4 – Полюсы и нули передаточной функции

Нули передаточной функции, расположенные на мнимой оси в точках , определяют снижение АЧХ в этих точках до нуля т.к. при и следовательно .