1.2Линейная цепь с постоянными параметрами

Линейной цепью с постоянными параметрами называют такую цепь, которая:

а) Состоит из элементов, параметры которых не зависят от внешних сил, действующих на цепь.

б) Подчиняется принципу суперпозиции (принципу наложения)

где это оператор, характеризующий воздействие цепи на входной сигнал. Принцип суперпозиции формулируют следующим образом: при воздействии на линейную цепь нескольких внешних сил поведение цепи (напряжение, ток) можно определить путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности. Принцип наложения лежит в основе спектрального и операторного методов анализа переходных процессов в линейных цепях, а так же метода наложения (интеграл Дюамеля). Применяя принцип наложения, любой сложный сигнал при передаче через линейную цепь можно разложить на простые сигналы, более удобные для анализа (например, гармонические).

в) Если при любом сколь угодно сложном воздействии в цепи не возникает колебаний новых частот (при прохождении через линейную цепь гармонического сигнала меняется только амплитуда и фаза этого сигнала).

Линейная цепь с постоянными параметрами применяется в задачах не связанных с преобразованием спектра (это линейные усилители, фильтры по частотному признаку и т.п.).

1.3Линейная цепь с переменными параметрами

Линейной цепью с переменными параметрами называют такую цепь, в которой один или несколько параметров изменяются во времени (но не зависят от входного сигнала). Такие цепи называют параметрическими. Гармоническое воздействие в этой цепи создает сложные колебания, имеющие свой спектр частот. Например:

- сопротивление;

- гармоническая э.д.с.;

- ток, протекающий через сопротивление.

В составе тока имеются элементы с частотами , которых нет во входном сигнале (спектр входного сигнала изменился). Похожие результаты получаются в цепях с реактивными элементами (емкости, индуктивности).

Линейные цепи с переменными параметрами применяют для создания параметрических усилителей, параметрических генераторов и т.п.

1.4Нелинейная цепь

Нелинейной цепью называют такую цепь, в которую входят один или несколько элементов параметры, которых зависят от уровня входного сигнала (например, диод см.Рис. 1.).

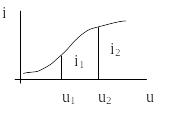
Рис. 1.3 – Характеристика нелинейного элемента

К основным свойствам нелинейных цепей относят:

а) Неприменимость принципа суперпозиции (в диоде сумма напряжений не соответствует сумме токов ). Методы анализа, основанные на принципе суперпозиции, не применимы.

б) Преобразование спектра сигнала. При воздействии гармонического сигнала помимо основной частоты возникают гармоники с частотами, кратными основной частоте (иногда добавляется постоянная составляющая). При воздействии сигнала сложной формы, помимо гармоник, возникают еще колебания с комбинационными частотами отдельных колебаний спектра сигнала.

В нелинейной цепи структура спектра сигнала на выходе зависит не только от формы входного сигнала, но и от его амплитуды. В линейной параметрической цепи структура спектра сигнала зависит от амплитуды входного сигнала.

Нелинейные цепи применяются для создания генераторов, детекторов, преобразователей частот и т.п.

Свойства цепей эти классов сохраняются при любых формах реализации:

• с сосредоточенными параметрами;

• с распределенными параметрами (передающие линии, излучающие устройства т.п.).

Принцип суперпозиции сформулирован для операции суммирования сигналов на входе цепи. На практике входной сигнал цепи может быть произведением двух сигналов. В этом случае обработку сигнала организуют по принципу сочетания нелинейной и линейной операций. Подобную обработку называют гомоморфной.

При анализе помех часто рассматривают линейную сумму полезного сигнала и шумовой помехи : . В этом случае помеху называют аддитивной, а называют аддитивной смесью сигнала и шума (например, дробовый шум, тепловой шум в электронных приборах).

При прохождении сигнала через реальный канал возникают искажения сигнала, связанные, например, с изменением во времени параметров цепи и других элементов канала. Упрощенно сигнал на выходе канала представляют в виде , где

- аддитивная помеха;

- коэффициент, характеризующий мультипликативную помеху.

Принцип суперпозиции, предусматривающий только операцию сложения сигналов, является основой для обработки аддитивной смеси сигналов, а также основой для спектрального метода анализа воздействия сложных сигналов на линейные цепи, для метода интеграла Дюамеля и других методов, в которых сигнал образуется как сумма элементарных сигналов.

Линейные цепи (системы) не позволяют осуществлять раздельную обработку сигналов, входящих в произведение или образующих свертку. По отношению к сигналам, вида , не применим принцип суперпозиции как в линейных системах. Преобразуем, этот сигнал к виду . Оператор преобразования обозначим символом . Задача сводится к требованию

Единственная непрерывная функция для этого равенства [ 2 ] это логарифм

,

где , .

Обозначим через и сигналы на выходе линейного фильтра , осуществляющего фильтрацию сигналов и . Сигналы и это логарифмы выходных сигналов и . Возникает задача перехода от сигнала к сигналу . Обратная функция к логарифму это экспонента. Обозначим экспоненту как тогда

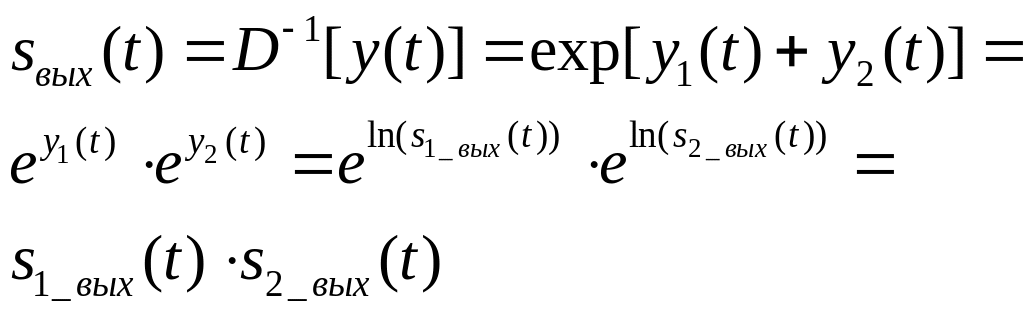
Между двумя нелинейными элементами ( и ) включено линейное устройство (+). Если спектры сигналов и не пересекаются, то тогда возможно разделение этих сигналов.

Преобразование сигнала в нелинейной системе для применения принципа суперпозиции показано на Рис. 1..

Рис. 1.4 – Нелинейная система. Принцип суперпозиции