Система дифференциальных уравнений
Алгебраические и дифференциальные уравнения, описывающие работу фильтра, составляются на основе законов Ома Кирхгофа (см. приложение 1.5).
Составление системы уравнений
Составим уравнения фильтра по контурам и узлам, показанным на Рис. 2.. Интегро-дифференциальные уравнения, составленные по контурам 1), 2), 3), выглядят следующим образом
,
алгебраическое уравнение, составленное по узлу а), выглядит следующим образом
.
Независимые
начальные условия определяем из
предположения о равенстве нулю напряжений
на всех конденсаторах и токов во всех
катушках индуктивности в момент времени
.
.
Зависимые начальные условия определяем из систем уравнений , ,
.
Дифференцируем, левые и правые части составленных интегро-дифференциальных уравнений, и получаем следующую систему линейных неоднородных дифференциальных уравнений с постоянными коэффициентами
.
Оставляем
два из трех дифференциальных уравнений
и вводим дополнительную переменную
.
Получаем следующую нормальную систему
линейных неоднородных дифференциальных
уравнений с постоянными коэффициентами
.
Полученная система уравнений, состоящая из трех дифференциальных уравнений и одного алгебраического уравнения, с полученными начальными условиями, может быть решена средствами пакета MathCad.
Решение системы средствами Odesolve
Для решения полученной системы уравнений используем встроенную процедуру Odesolve.
На Рис. Г. представлена процедура интегрирования полученных уравнений со следующими исходными данными:
R, C, L, Rn – значения величин элементов;
t - переменная интегрирования;
dlt ( ) - шаг интегрирования;
steps - число шагов интегрирования;
T1 - время интегрирования;
e(t) - единичное входное воздействие.
Результат интегрирования полученных уравнений представлен на Рис. Г..
Рис. Г.4 – Процедура интегрирования системы Odesolve
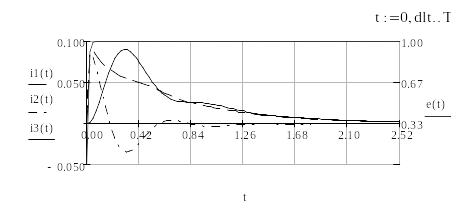
Рис. Г.5 – Результаты интегрирования системы. Odesolve
Преобразуем полученную систему уравнений в систему разностных уравнений по методу Эйлера.
Система разностных уравнений
Заменим производную в нормальной системе дифференциальных уравнениях следующей разностью
,
и получим следующую систему разностных уравнений
.
Оставим в левой части уравнения старшие (по времени) переменные и соберем в правой части все другие переменные
.
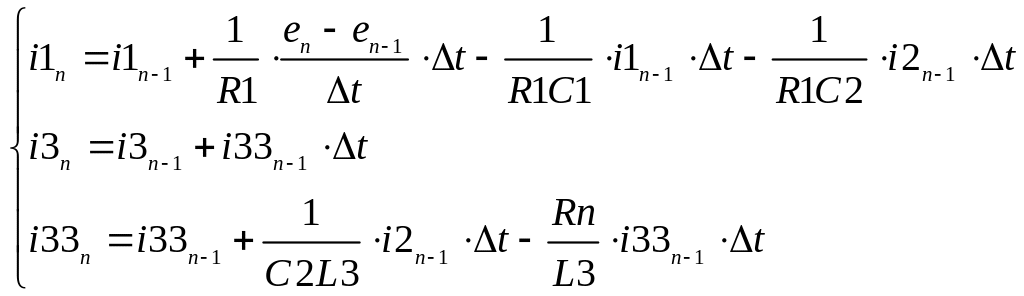Добавим в полученную разностную схему алгебраическое уравнение, упростим систему уравнений и учитывая начальные условия напишем, средствами пакета MathCad, процедуру интегрирования Mysolve.
Решение системы разностных уравнений
Процедура интегрирования разностных уравнений Mysolve представлена на Рис. Г.. Результат интегрирования уравнений системы Mysolve представлена на Рис. Г..
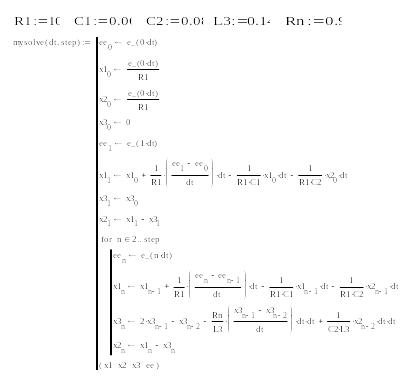
Рис. Г.6 – Процедура интегрирования системы Mysolve
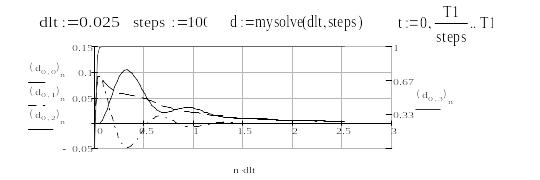
Рис. Г.7 – Результаты интегрирования системы. Mysolve
Сравнение полученных решений
Сравним результаты решений системы процедурами Odesolve и Mysolve путем наложения графиков решений, полученных этими процедурами. Отобразим графики переменной , на одной временной оси (см.Рис. Г.).
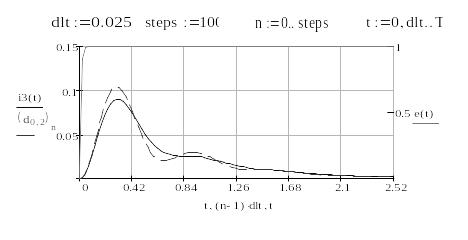
Рис. Г.8 – Сравнение результатов интегрирования системы
Предполагая, что стандартная процедура Odesolve дает более точное решение, чем процедура Mysolve, с помощью рисунка можно оценить точность интегрирования по схеме Эйлера.