Построение выражений и их вычисление
Перед работой в MathCad курсор имеет вид крестика. В момент ввода выражения курсор имеет вид синего уголка, охватывающего вводимое выражение. Имя выражения может состоять из латинских, русских, греческих и других букв и цифр, знаков подчеркивания (_), штриха (`), символа процента (%), знака бесконечности, вводимых с клавиатуры.
Имена переменных и функций не могут начинаться с цифры, знака подчеркивания, штриха, символа процента (%), также не могут включать в себя пробелы. Символ бесконечности может быть только первым символом в имени.
Mathcad воспринимает заглавные и строчные буквы как различные идентификаторы, это же касается букв, изображенных разными шрифтами.
В Mathcad нет различий между именами переменных и функций. Если определить сначала функцию f(x), а потом переменную f, окажется невозможным использовать f(x) в последующих расчетах где-либо ниже определения f.
Некоторые имена уже используются Mathcad для встроенных констант, единиц измерения, функций. Имена можно переопределить, но это уничтожит их встроенные значения и этими константами, функциями пользоваться будет нельзя.
Оператор присваивания (:=) расположен на математической панели Calculator (Рис. Б.). В дальнейшем оператор присваивания лучше набирать с клавиатуры, нажав клавишу «двоеточие» (:).
Набрав вычисляемое выражение, нажмите клавишу (=) — появится численный результат (Рис. Б.).
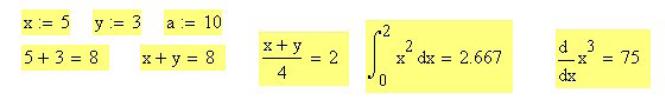
Рис. Б.3 – Пример построения математических выражений
Цепкие операторы — это возведение в степень, извлечение корня, знаменатель дроби (Рис. Б.). Чтобы вырваться из цепкого оператора, необходимо выделить клавишей пробел или клавишей → (стрелкой вправо) нужную часть выражения, тогда следующая вводимая операция будет относиться ко всему выделенному выражению.
Рис. Б.4 – Построения выражений «с цепкими операторами»
Редактирование объектов Mathcad введенных выражений производится обычным для всех Windows-приложений способом
Стандартные функции
Удобство и эффективность расчетов в Mathcad прежде всего определяется возможностью и легкостью создания функций.
Как правило, функция имеет следующий вид: слева название функции (с параметрами в скобках), справа, после оператора присваивания :=, вычисляемое выражение.
Переменные величины должны быть записаны в параметры после имени функции в скобках. Все величины из правой части, которые не входят в параметры левой части, должны быть заданы численно левее и выше функции. В противном случае Mathcad указывает на ошибку.
Дискретная переменная. Дискретная переменная, выполняет роль оператора цикла. Использование дискретной переменной позволяет построить графики, вывести таблицы результатов расчета. Дискретная переменная определяет ряд значений переменной, для которых вычисляется функция. Этот ряд значений функции можно вывести в виде графика или таблицы.
Дискретная переменная может задавать целые, и дробные значения переменной, но обязательно равноотстоящие друг от друга, например: x:=0..5– ряд целых чисел от 0 до 5
x := 1,1.1..5 = – ряд дробных чисел, где 1 – первое число, 1.1 – второе число, 5 – последнее число. Интервал между числами 1.1-1 =0.1.
Две точки – знак диапазона нельзя набирать с клавиатуры. На клавиатуре необходимо нажать клавишу ; (точка с запятой) или в математической панели выбрать Matrix (значок матрицы) m..n.
Форматирование чисел. Форматирование чисел позволяет изменить формат вывода чисел.
Mathcad вычисляет выражения с точностью до 20 знаков, но при этом выводит не все значащие цифры.
Сделав двойной щелчок левой кнопкой мыши, на нужном месте численного результата расчета, откроется окно форматирования чисел Result Format (Формат результата), на пункте Number Format (Формат чисел). В окне можно выбрать следующие форматы:
General (Основной) – Число знаков перед запятой определяется Exponential threshold (Порог экспоненты).
Decimal (Десятичный) – представление чисел с плавающей запятой: 12.2564.
Scientific (Научный) – с порядком: 1.22*105.
Engeneering (Инженерный) – с порядком, кратным 3: 1.22*106.
Fraction (Дробный) – в виде правильной или неправильной дроби: 53 или 213 .
В дробном формате можно выбрать уровень точности (Level of accuracy) и смешанные числа (Use fixed number).
Кроме формата числа, можно менять число знаков после запятой (Number of decimal pieces), порядковый порог (Exponential threshold). Примеры вывода чисел в различных форматах приведены на Рис. Б.. Mathcad округляет числа до нуля, если они меньше установленного порога. Выбранные установки применяются либо для выделенного числа, либо по умолчанию ко всем числам данного документа (пункт Set as default – применить по умолчанию).
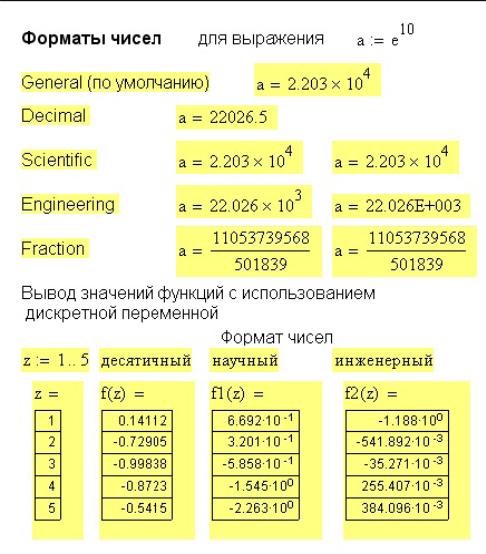
Рис. Б.5 – Примеры форматирования результата численного расчета
Построение плоского графика функции
Для того, чтобы построить плоский график функции надо:
Установить курсор в то место, где необходимо построить график.
На математической панели выбрать кнопку Graph Toolbar X-Y Plot (Плоский график).
В шаблоне плоского графика, появившегося на месте курсора вводится на оси абсцисс имя аргумента, на оси ординат – имя функции.
Щелкните вне шаблона графика мышью. График построен для заданного диапазона изменения аргумента.
Если диапазон значений аргумента не задан, то график будет построен автоматически в диапазоне значений аргумента от –10 до 10 .
Чтобы разместить несколько графиков в шаблоне, надо набрать на оси ординат имя первой функции, нажать клавишу запятая, и в появившемся месте ввода вписать имя второй функции и т.д.
Если несколько функций имеют разные аргументы, f(x) и f(y), то на оси ординат через запятую вводятся имена обеих функций, а на оси абсцисс – имена обоих аргументов x и y. Первый график будет построен для первой функции по первому аргументу, второй график для второй функции по второму аргументу и т.д.
Если функций несколько, а аргументов два, то первый график строится по первому аргументу, а графики остальных – по второму.
Если на осях абцисс и ординат ввести имена двух функций одного аргумента, то строится параметрический график функции (Рис. Б.)
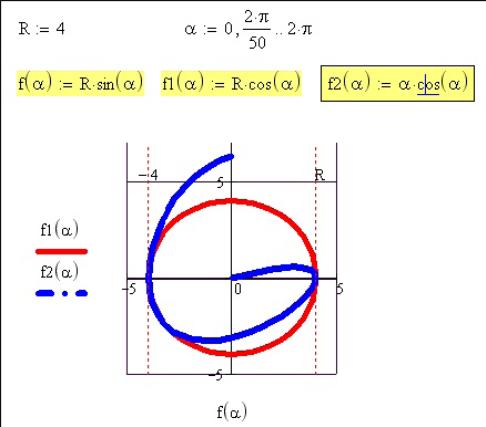
Рис. Б.6 – Параметрический график функции
Для того, чтобы отформатировать график, необходимо щелкнуть дважды мышкой в поле графика– откроется окно форматирования графика.
Рис. Б.7 – Окно форматирования плоского графика
В открывшемся окне (Рис. Б.) видны четыре вкладки:
X-Y Axes –форматирование оси координат:
Log Scale –численные значения на осях в логарифмической шкале.
Grid Lines – нанести сетку линий.
Numbered –численные значения для каждой линии сетки.
Auto Scale – автоматически выбираются предельные значения на осях, большие максимальных вычисленных значений. Предельными будут максимальные вычисленные значения. Если этот пункт не отмечен.
Autogrid – число линий сетки. Необходимо задать число линий Number of Grids, если этот пункт не отмечен.
Show Markers – метки на графике. На каждой оси появляются 2 места ввода, в которые можно ввести численные значения. На графике появятся горизонтальные или вертикальные пунктирные линии, соответствующие значению на оси. В конце линии появляется само число (Рис. Б.).
Trace – отформатирование графиков функций. Для каждого графика по отдельности можно изменить: вид линии, цвет линии (Color), тип графика, толщину линии (Weight).
Расчетные точки можно отметить различным символом на графике (Symbol).
Также можно Вписать в область графика заголовок (Label). В окне Tytle (Заголовок) – текст заголовка. Выбрать его положение, а также если необходимо вписать названия аргумента и функции (Axis Label).
Defaults – вернуться к виду графика, принятому по умолчанию (Change to default), или сделанные вами изменения применить по умолчанию для всех графиков данного документа (Use for default).
Если выражения или графики накрывают друг друга, в контекстном меню появляются пункты Bring to Front (Выдвинуть на передний план) и Send to Back (Убрать на задний план). Использование этих пунктов позволяет экономить место в документе.
Если необходимо раздвинуть наложившиеся друг на друга объекты, сначала выделите эти объекты, перечеркнув их мышью при нажатой левой кнопке, затем в главном меню Mathcad выберите Format Separate Region (Разделить Области). Только выделенные области при этом будут раздвинуты.
Если надо раздвинуть два объекта, подведите к объекту курсор. При появлении черной ладошки нажмите левую кнопку мыши и, двигая мышь, переместите объект в нужное место.
Полярный график
Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (Рис. Б.2) и вставить в местозаполнители имена переменных и функций. Которые будут нарисованы в полярной системе координат: угол (нижний местозаполнитель) и радиус-вектор (левый местозаполнитель). Точно так же, как и при создании плоского графика, по осям могут быть отложены два вектора (Рис. Б.8, слева), элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое постороение графика функции (Рис. Б.8, справа)
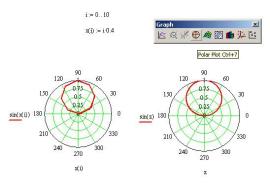
Рис. Б.8 – Полярные графики
Форматирование полярных графиков практически идентично форматированию плоских, поэтому все, сказанное выше об оформлении двухмерных графиков, в полной мере относится и к полярным.
Решение дифференциальных уравнений
Решение дифференциальных уравнений — очень сложная проблема. Mathcad не может решить без дополнительных упрощений дифференциальные уравнения и их системы. Рассмотрим функцию odesolve. Имя функции odesolve можно писать как с прописной, так и со строчной буквы. Алгоритм функции odesolve использует большинство, имеющихся функций решения дифференциальных уравнений, фактически заменяя их.
В Mathcad присутствует много различных функций для решения дифференциальных уравнений. Функция odesolve позволяет записывать уравнение в привычном виде.
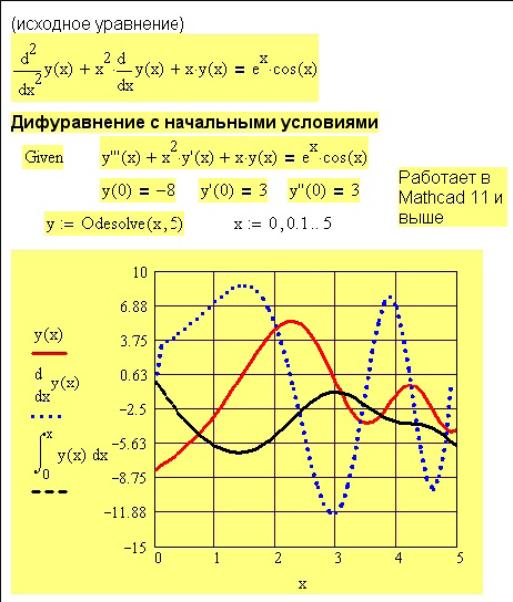
Рис. Б.9 – Решение дифференциального уравнения с начальными условиями
Функция odesolve требует записи, состоящей из трех частей:
1. ключевое слово given (дано);
2. дифференциальное уравнение и начальные (граничные) условия к нему, граничные условия следует записывать только со штрихом;
3. функция odesolve(x, xk, n), где
x — имя переменной, относительно которой решается уравнение;
xk — конец интервала интегрирования. Начало интервала указано в начальных условиях;
n —параметр, определяющий число шагов интегрирования, на которых вычисляется решение дифференциального уравнения.
Чем больше n, тем больше точность решения уравнения. Параметр n не является обязательным. Если его удалить, Mathcad сам выберет число шагов интегрирования.
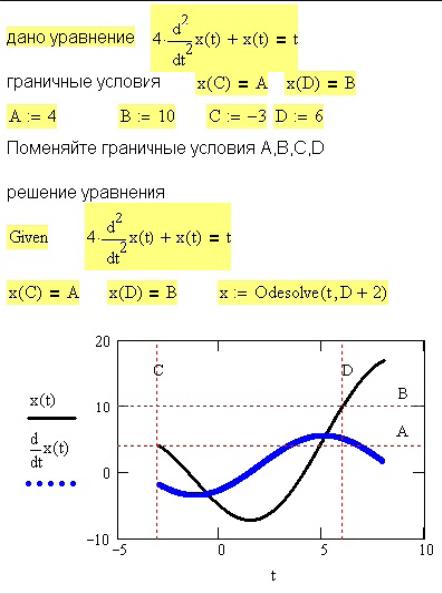
Рис. Б.10 – Решение дифференциального уравнения с граничными условиями
Функция odesolve возвращает решение дифференциального уравнения в виде функции, поэтому найденное решение можно интегрировать, дифференцировать (см. Рис. Б.9 – Рис. Б.10Рис. Б.), и использовать в последующих расчетах.
Функция odesolve решает дифференциальные уравнения как с начальными условиями, так и с граничными. Начальные условия задаются в начале интервала интегрирования, граничные же в двух точках, одна из которых обязательно является началом интервала интегрирования, вторая – произвольная и аргумент её больше, чем в начальной точке. Решение уравнения с начальными условиями показано на Рис. Б.9, с граничными условиями — на Рис. Б.10.
Решение системы дифференциальных уравнений показано на Рис. Б.11. Как видно, обращение к функции odesolve изменилось. Для решения одного уравнения: odesolve(x, xk, n).
Для решения системы дифференциальных уравнений: odesolve( (вектор имен неизвестных), x, xk, n).
На Рис. Б.11 при решении системы трех уравнений вектор имен неизвестных содержит 3 имени.
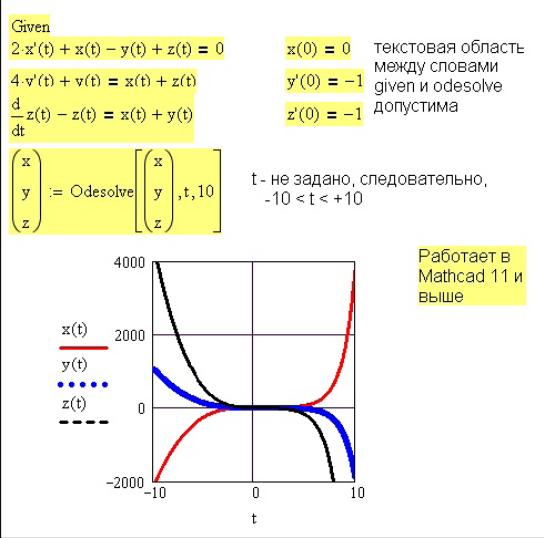
Рис. Б.11 – Решение системы дифференциальных уравнений с начальными условиями