7. Сигналы с ограниченной полосой частот

В теории сигналов используют теорему Котельникова (теорема отсчетов). Эта теорема формулируется следующим образом [ 2 ]:

Если наивысшая частота в спектре функции меньше чем , то функция полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на секунд.

В соответствии с этой теоремой сигнал , ограниченный по спектру наивысшей частотой , может быть представлен рядом

.

В этом выражении обозначает интервал между двумя отсчетными точками на оси времени, а обозначает выборки функции в моменты времени . Функция вида

обладает следующими свойствами:

• в точке функция , а в точке , где это любое целое положительное или отрицательное число, отличное от , ;

• спектральная плотность функции равномерна в полосе частот и равна .

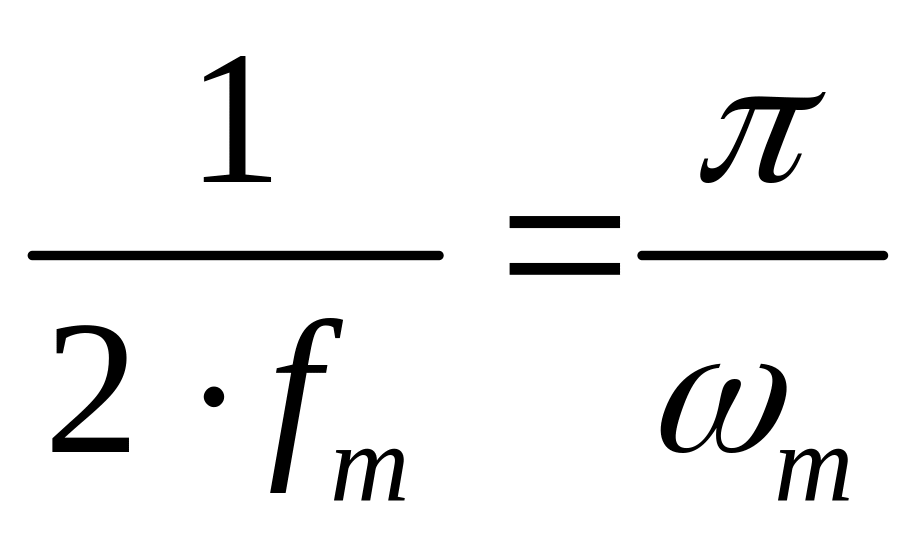Так как функция отличается от только сдвигом на оси времени на , то спектральная плотность функции будет

.

Очевидно, что ряд представляющий функцию , точно определяет в точках отсчета поскольку коэффициентами ряда являются сами выборки из этой функции (величины ). Для доказательства того, что ряд определяет функцию в любой момент , а не только в точках отсчета воспользуемся правилами разложения функции по ортогональной системе. В этом случае разложение производится по функциям вида для которых интервал ортогональности равен бесконечности, а норма равна

.

Общая формула определения значений коэффициентов ряда, справедливая для обобщенного ряда Фурье выглядит следующим образом

.

При этом предполагается, что это квадратично-интегрируемая функция (энергия сигнала конечна). Для определения коэффициентов воспользуемся следующей формулой [ 2 ]

.

Окончательно получим следующее выражение , из которого следует, что коэффициентами ряда являются выборки функции в точках . Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции , то ряд сходится к функции при любом значении .

Если взять интервал между выборками меньше чем , то ширина спектра функции будет больше, чем у спектра функции . Это повысит точность представления сигнала и ослабит требования к АЧХ фильтра, восстанавливающего непрерывный сигнал.

При увеличении по сравнению с спектр функции становится уже, чем спектр функции . Коэффициенты при этом являются уже выборками не заданного сигнала , а некоторой другой функции , спектр которой ограничен наивысшей частотой .

В случае, когда длительность сигнала конечна и равна , а полоса частот по-прежнему равна , мы имеем дело, строго говоря, с несовместимыми условиями, так как функция конечной длительности обладает теоретически бесконечно широким спектром.

На практике всегда можно определить наивысшую частоту спектра так, что бы потери энергии, обусловленные отсечением частот, превышающих , содержали пренебрежительно малую долю энергии по сравнению с энергией исходного сигнала .

При таком допущении для сигнала длительностью с полосой частот общее число независимых параметров (число значений ) которое необходимо для полного задания сигнала очевидно будет

.

При этом значение функции будет вычисляться по следующей формуле (при отсчете времени от первой выборки)

.

Число иногда называют числом степеней свободы сигнала , так как даже при произвольном выборе значений сумма определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности интервала времени . Число иногда называют также базой функции.

Энергия сигнала вычисляется (с учетом ) по формуле

.

Средняя мощность сигнала вычисляется по формуле

.

Средняя за время мощность непрерывного сигнала равна среднему квадрату выборок, число которых .

В том случае, когда сигнал необходимо представить с помощью частотных выборок спектральной функции , а не временных выборок функции для функции можно составить ряд с базисной функцией

который выглядит следующем образом

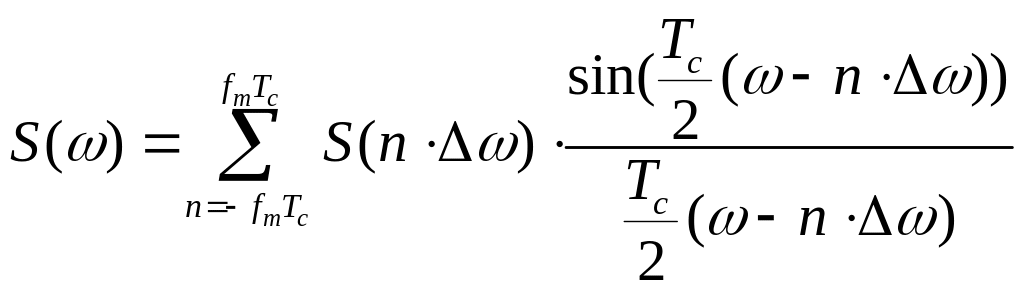
Используя равенство схожее с получим

.

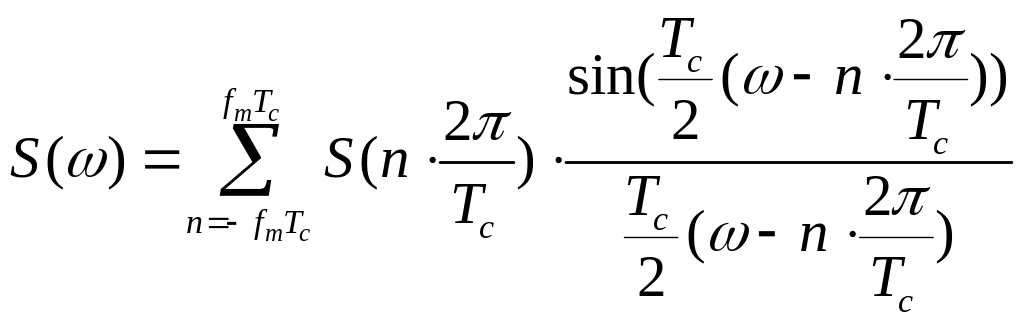Если временной интервал между двумя соседними выборками не должен превышать , то частотный интервал не должен превышать . При ширине спектра , охватывающий область частот , число выборок равно .

В общем случае выборки являются комплексными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра (действительная и мнимая части). Если учесть, что и комплексно-сопряженные функции, то задание одной из них однозначно определяет другую. В этом случае спектр сигнала полностью характеризуется совокупностью комплексных выборок, взятых только в области положительных частот с числом независимых параметров или степеней свободы сигнала , как и представлении сигнала во временной области.