Переходные процессы
Переходные (нестационарные) процессы возникают в результате коммутаций, происходящих в электрических цепях. Под коммутацией понимают различные включения, выключения, переключения пассивных и активных ветвей и элементов электрической цепи, приводящие к изменению схемы или ее параметров. Считают, что коммутация совершается мгновенно. Для момента коммутации существуют следующие правила.
Ток и магнитный поток в ветви с индуктивным элементом не могут изменяться скачком, и в момент коммутации равны тем значениям, которые они имели непосредственно перед коммутацией. Условия непрерывности тока и магнитного потокосцепления в цепи с индуктивным элементом Рис. А.:
,
,
.
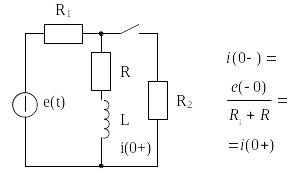
Рис. А.4 – Схема коммутации с индуктивностью
Напряжение и заряд на емкостном элементе не могут изменяться скачком, и в момент коммутации равны тем значениям, которые они имели непосредственно перед коммутацией. Условия непрерывности напряжения и заряда в цепи с емкостным элементом Рис. А.:
,
,
.
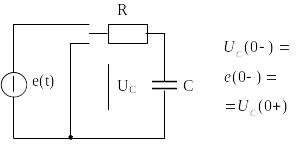
Рис. А.5 – Схема коммутации с емкостью
Независимые начальные условия (значение тока или потока в индуктивном и напряжения или заряда на емкостном элементах в момент коммутации) определяются по законам коммутации.
Зависимые начальные условия (значения токов и напряжений в момент коммутации) определяются по схеме, образованной после коммутации по законам Кирхгофа с учетом законов коммутации.
Независимые и зависимые начальные условия схемы, представленной на Рис. А. будут следующие:
независимые
начальные условия для тока
;
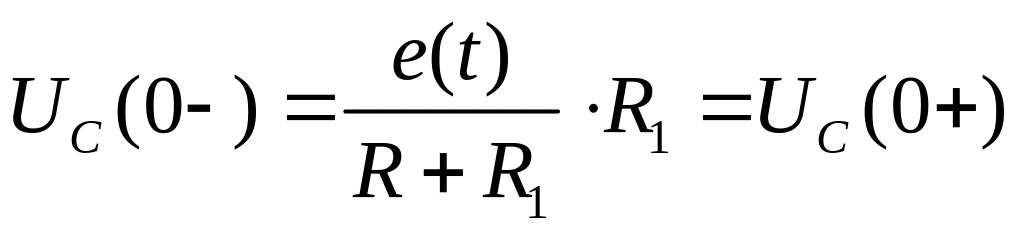независимые
начальные условия для напряжения
.
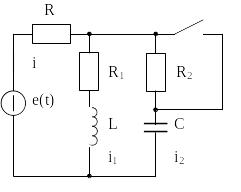
Рис. А.6 – Зависимые начальные условия
Для
определения зависимых начальных условий
используем законы Кирхгофа и определенные
ранее значения тока и напряжения
,
.
Для цепей, образованных после коммутации,
составим уравнения Кирхгофа с учетом
значений
,
.
Полученную
систему алгебраических уравнений решим
относительно искомых величин
,
,
.
зависимые начальные условия для токов , ;
зависимые
начальные условия для производной
.
Для расчета переходных процессов на цифровых вычислительных машинах используют, как наиболее удобный, метод переменных состояний. Для после коммутационной схемы, вместо одного неоднородного дифференциального уравнения n-го порядка, решают n дифференциальных уравнений первого порядка относительно выбранных переменных. Переменными могут быть напряжения на конденсаторах, токи в индуктивных катушках, и другие величины, по начальным состояниям которых (и входным воздействиям) определяют искомые переходные функции.
В
качестве примера рассмотрим переходный
процесс в последовательном колебательном
контуре (Рис. А.). Ток в схеме является
общим для всех элементов схемы. Считаем
начальные условия нулевыми
,
.
В схеме до коммутации нет запаса энергии.
Независимые
начальные условия схемы будут следующие
,
,
.
Зависимые
начальные условия схемы вычисляются
из следующих соображений
.
Интегро-дифференциальное уравнение контура, составленное по второму закону Кирхгофа и закону Ома, будет выглядеть так:
.
Дифференцируя левую и правую части этого уравнения, получим следующее дифференциальное уравнение второго порядка
.
Система из двух дифференциальных уравнений первого порядка будет выглядеть так:
.
Такая система дифференциальных уравнений, решаемая численными методами, может использоваться микропроцессорной системой, для обработки входного сигнала в реальном времени.