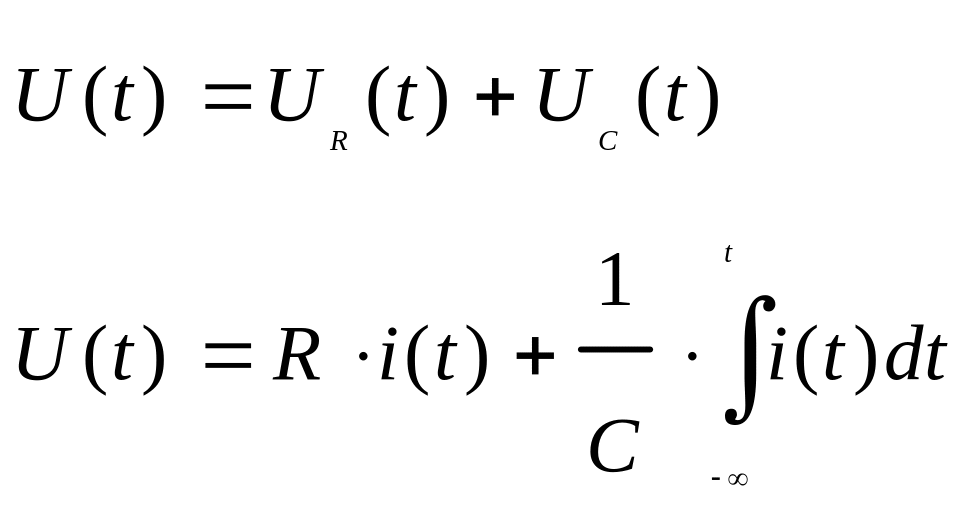Законы Ома и Кирхгофа
Для описания электрической цепи (совокупности устройств и объектов, образующих путь для электрического тока) используют некоторую эквивалентную схему. Выделяют следующие топологические элементы [ 6 ], образующие схему электрической цепи.
Ветвью называют участок электрической цепи, вдоль которого протекает один и тот же ток.
Узлом называют место соединения ветвей электрической цепи.
Контуром называют любой замкнутый путь, образованный узлами и ветвями.
Графом называют изображение схемы электрической цепи, в котором ветви схемы представлены отрезками (ветвями графа), а узлы представлены точками (узлами графа).
Деревом называют любую совокупность ветвей графа, соединяющих все узлы графа без образования контуров.
Первый закон Кирхгофа говорит о том, что алгебраическая сумма токов в узле равна или нулю или алгебраической сумме источников тока в том же узле
,
.
Число линейно независимых уравнений, составленных по первому закону Кирхгофа, равно n-1, где n это число узлов рассматриваемой схемы.
Второй закон Кирхгофа говорит о том, что алгебраическая сумма падений напряжений в любом замкнутом контуре схемы равна или нулю или алгебраической сумме э.д.с. в этом контуре
,
.
Число линейно независимых уравнений, составленных по второму закону Кирхгофа, равно m-n+1, где m это число ветвей, а n это число узлов рассматриваемой схемы.
Закон Ома для участка цепи, содержащей сопротивление, емкость и индуктивность выглядит следующим образом:
для
комплексного значения гармонического
тока и напряжения;
,
,
для тока и напряжения как функции
времени.
Формулы вычисления значений последовательного и параллельного соединения сопротивлений, представлены в Табл. А.1.
Частотные и мгновенные временные характеристики цепей представлены в Табл. А.2.
Табл. А.1 – Соединения сопротивлений
Обозначение |
Вычисление |
Описание |
|
|
Последовательное соединение |
|
|
Параллельное соединение |
Табл. А.2 – Частотные и временные характеристики цепей
Обозначение цепи |
Частотная область |
Временная область |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим применение законов Ома и Кирхгофа для составления алгебраических уравнений в частотной области и интегро-дифференциальных уравнений во временной области на примере схемы последовательного R, C, L контура (Рис. А.).
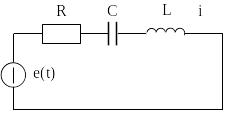
Рис. А.3 – Последовательный R, C, L контур
В
частотной области, при гармоническом
входном воздействии
,
уравнение составлено по второму закону
Кирхгофа будут выглядеть следующим
образом
.
Ток
в цепи вычислим по формуле
.
Напряжение
на индуктивном элементе
вычислим по формуле
учитывая, что
,
,
получим выражение
.
Выделив, вещественную и мнимую части выражения, получим
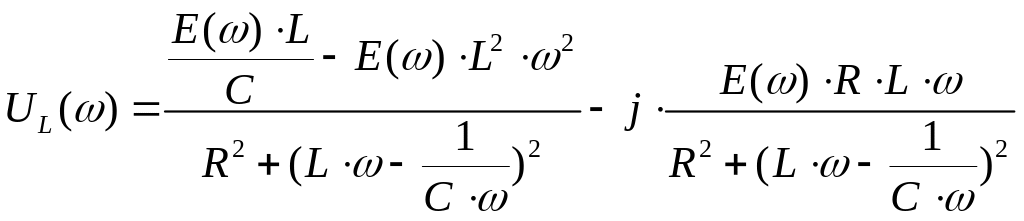
алгебраическую форму комплексного числа (зависящего от частоты ) для напряжения .
Выделив, вещественную и мнимую части выражения, получим
алгебраическую форму комплексного числа, зависящего от частоты , для напряжения .
Во временной области уравнение, составленное по второму закону Кирхгофа, представлено в главе 3.2 и приложении 1.6.