
- •Сокращения
- •Введение
- •1Виды сигналов и цепей
- •1.1Континуальные и дискретные сигналы
- •1.2Линейная цепь с постоянными параметрами
- •1.3Линейная цепь с переменными параметрами
- •1.4Нелинейная цепь
- •2Линейная фильтрация сигнала
- •2.1Классификация фильтров
- •2.2Частотные характеристики фильтров
- •2.3Фильтры второго порядка
- •Фильтры нижних частот
- •Фильтры верхних частот
- •Полосно-пропускающие фильтры
- •Частотно-заграждающие фильтры
- •Частотно-выделяющие фильтры
- •Всепропускающие фильтры
- •2.4Работа т-образного фильтра
- •3Цифровая обработка сигнала
- •3.1Структура цифровых ких и бих фильтров
- •3.2Интегрирование уравнений методом Эйлера
- •3.3Интегрирование уравнений методом Адамса
- •3.4Интегрирование системы уравнений
- •3.5Построение цифровых бих фильтров
- •4Аппаратные средства aTmega 8535 avr
- •4.1Функциональная схема архитектуры
- •4.2Специальные функции контроллера
- •4.3Основные характеристики периферии
- •4.4Память программ и данных
- •4.5Тактовый генератор и таймеры
- •4.6Периферийные устройства
- •4.7Модуль прерываний
- •4.8Порты контроллера
- •4.9Режимы пониженного энегопотребления
- •7.2Вторая часть задания
- •7.3Третья часть задания
- •Заключение Литература
- •Термины и определения
- •Линейные пространства
- •Дифференциальные уравнения
- •Комплексные числа
- •Гармонические функции
- •Законы Ома и Кирхгофа
- •Переходные процессы
- •Сигналы с ограниченной полосой частот
- •Средства пакета MathCad
- •Интерфейс MathCad
- •Построение выражений и их вычисление
- •Стандартные функции
- •Ввод греческих букв
- •Ввод текста
- •Варианты заданий
- •Пример выполнения задания
- •Частотные характеристики фильтра
- •Система дифференциальных уравнений
- •Составление системы уравнений
- •Решение системы средствами Odesolve
- •Система разностных уравнений
- •Решение системы разностных уравнений
- •Сравнение полученных решений
- •Дифференциальное уравнение 3-го порядка
- •Получение дифференциального уравнения
- •Сравнение частотных характеристик
- •Решение уравнения средствами Odesolve
- •Разностное уравнение
- •Решение разностного уравнения
- •Сравнение полученных решений
- •Программирование в среде Code Vision avr
- •Решение системы по разностной схеме
- •Результаты решения системы
- •Выводы по проделанной работе
Комплексные числа
Комплексным
числом называют [ 1, 2, 6 ] сумму
действительного и мнимого чисел
![]() (
(![]() и
и
![]() – действительные числа,
– действительные числа,
![]() - мнимая единица). Мнимую единицу (
)
определяют следующим образом:
- мнимая единица). Мнимую единицу (
)
определяют следующим образом:
![]() .
Мнимая единица обладает свойствами:
.
Мнимая единица обладает свойствами:
![]() ,
,
![]() ,
и т.д.
,
и т.д.
Два
комплексных числа
и
![]() считают равными, если равны их
действительные (
считают равными, если равны их
действительные (![]() )
и мнимые (
)
и мнимые (![]() )
части.
)
части.
Два
комплексных числа
и
![]() называют сопряженными.
называют сопряженными.
Комплексное
число можно представить вектором на
комплексной плоскости (Рис. А.), проведенным
из начала координат
![]() в точку
в точку
![]() .
.
Длину
вектора (![]() ),
изображающего комплексное число,
называют модулем этого числа (
),
изображающего комплексное число,
называют модулем этого числа (![]() ).
Аргументом комплексного числа (
)
называют угол между осью действительных
значений и вектором, изображающим
комплексное число (
).
Аргументом комплексного числа (
)
называют угол между осью действительных
значений и вектором, изображающим
комплексное число (![]() ).
).
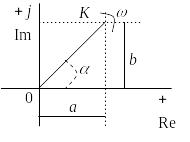
Рис. А.1 – Комплексная плоскость
Вещественную
и мнимую части комплексного числа
обозначают следующим образом
![]() .
.
Выделяют алгебраическую, показательную и тригонометрическую формы представления комплексного числа:
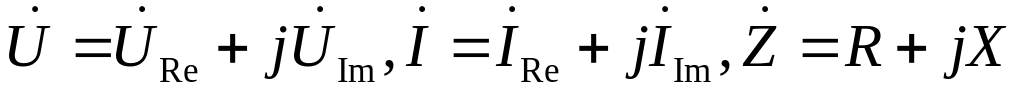 алгебраическая
форма;
алгебраическая
форма;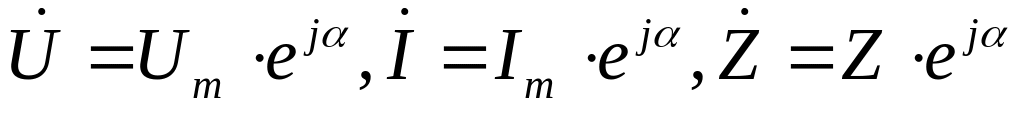 показательная
форма;
показательная
форма;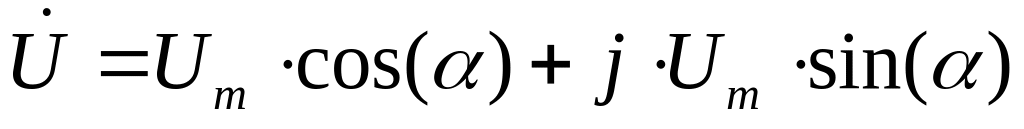 тригонометрическая
форма.
тригонометрическая
форма.
Алгебраическая форма удобна при сложении и вычитании комплексных чисел:
![]() ,
,
![]() .
.
Показательная форма удобна при умножении, делении, извлечении корня и логарифмирования комплексных чисел:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тригонометрическая форма удобна при переходе от показательной формы к алгебраической форме комплексного числа:
![]() ,
,
![]() .
.
Умножение
комплексного числа на величину
![]() приводит к повороту вектора комплексного
числа против (по) часовой стрелки на
приводит к повороту вектора комплексного
числа против (по) часовой стрелки на
![]() без изменения длины вектора.
без изменения длины вектора.
Сопротивление,
содержащее активную и реактивную
составляющую, представляют как комплексное
число
![]() (
(![]() -
активная,
-
активная,
![]() -
реактивная часть).
-
реактивная часть).
Гармонические функции
Гармоническим током (напряжением) называют ток, периодически изменяющийся во времени по синусоидальному закону [ 1, 6 ]. Мгновенное значение гармонического тока определяет следующим выражением
![]() ,
где:
,
где:
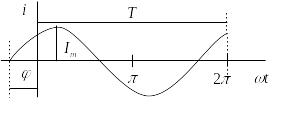
Рис. А.2 ‑ Гармоническая функция
 амплитуда
гармонического сигнала (максимальное
значение);
амплитуда
гармонического сигнала (максимальное
значение);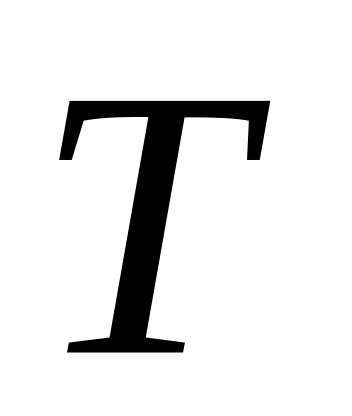 период
гармонического сигнала (время
одного
колебания);
период
гармонического сигнала (время
одного
колебания);
угловая частота (скорость изменения фазы);
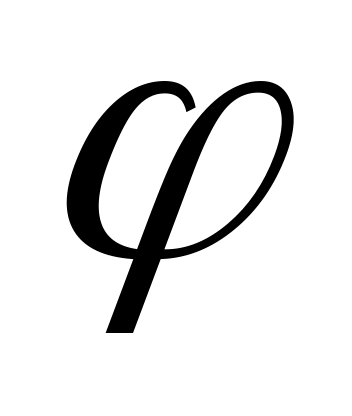 начальная
фаза (значение фазы в момент времени
);
начальная
фаза (значение фазы в момент времени
);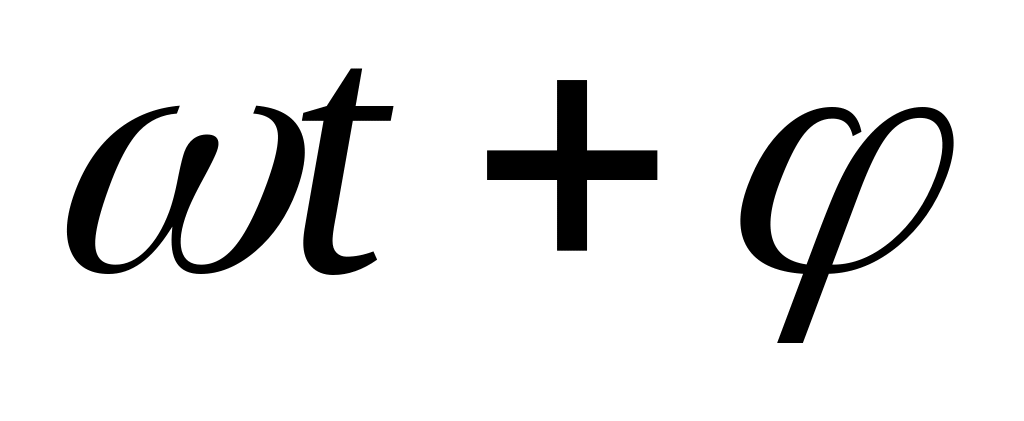 фаза
(аргумент синусоидального сигнала).
фаза
(аргумент синусоидального сигнала).
График гармонической функции представлен на Рис. А..
Мгновенное значение гармонического сигнала заменяют комплексным значением, например:
![]() ,
,
![]() .
.
Комплексную
величину, представляющую гармоническую
функцию времени, отмечают точкой наверху
(![]() ).
Иногда комплексные величины подчеркивают
снизу (
).
Иногда комплексные величины подчеркивают
снизу (![]() ).
).
Для описания работы линейной электрической схемы гармонического тока в установившемся режиме используют систему алгебраических уравнений, составленных по методам, основанным на законах Ома и Кирхгофа [ 3 ].
Для
алгебраизации интегро-дифференциальных
уравнений применяют комплексные
величины. В этих уравнениях дифференцирование
и интегрирование мгновенного значения
переменных заменяют умножением
комплексных величин этих переменных
на комплексные числа
и
![]() соответственно:
соответственно:
![]() ,
,
![]()
![]() ,
,
![]() .
.
Полученную таким образом систему алгебраических уравнений можно решать относительно неизвестных комплексных величин.
