Дифференциальные уравнения
Дифференциальным
уравнением называют уравнение [ 5 ],
связывающее независимую переменную
,
искомую функцию
и ее производные
,
,…,
.
Линейным уравнением первого порядка называют уравнение, линейное относительно неизвестной функции и ее производной
.
Дифференциальное уравнение n-го порядка называют линейным (уравнение первой степени относительно совокупности искомой функции и ее производных), если оно имеет вид
,
где
,
,…,
и
это заданные функции от
или постоянные, причем
для всех значений
из области определения уравнения. Обычно
уравнение приводят к виду с коэффициентом
.
Функцию
называют правой частью уравнения.
Если
,
то уравнение называют линейным
неоднородным или уравнением с правой
частью.
Если
,
то уравнение имеет вид
и называется линейным однородным или уравнением без правой части (левая часть этого уравнения является однородной функцией первой степени относительно , , ,…, ).
Если
для всех
отрезка
имеет место равенство
,
где
,
,
это постоянные числа, не равные нулю,
то говорят, что
выражается линейно через функции
,
,…
.
функций , ,… , называют линейно независимыми, если никакая функция из этих функций линейно не выражается через остальные.
Систему дифференциальных уравнений, в которой в левой части уравнений стоят производные первого порядка, а правые части не содержат производных,
,
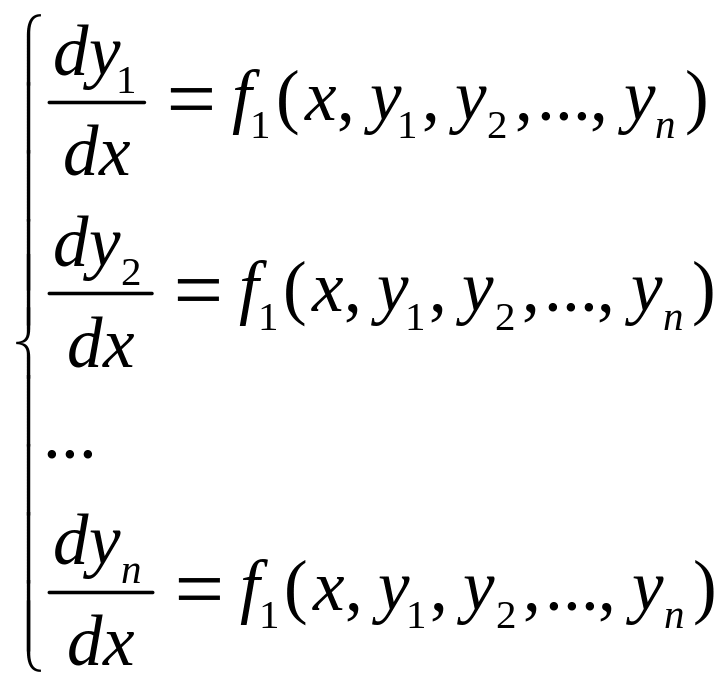где , ,… искомые функции, а это аргумент, называют нормальной.
Систему
дифференциальных уравнений, в которой
коэффициенты
это постоянные,
это аргумент, а
,
,…
это искомые функции
,
называют системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Проинтегрировать
систему дифференциальных уравнений
(например, нормальную систему) это значит
определить функции
,
,…
,
удовлетворяющие заданной системе
уравнений и начальным условиям:
,
,…
.
Интегрирование нормальной системы
можно производить следующим образом.
Дифференцируем по
первое из уравнений
.
Заменяем
производные
,
,…
их выражениями
,
,…
из нормальной системы уравнения получим
уравнение
.
Дифференцируя полученное уравнение и делая аналогичные замены, получим уравнение
.
Дифференцируя далее и производя замены, получим следующую систему дифференциальных уравнений
.
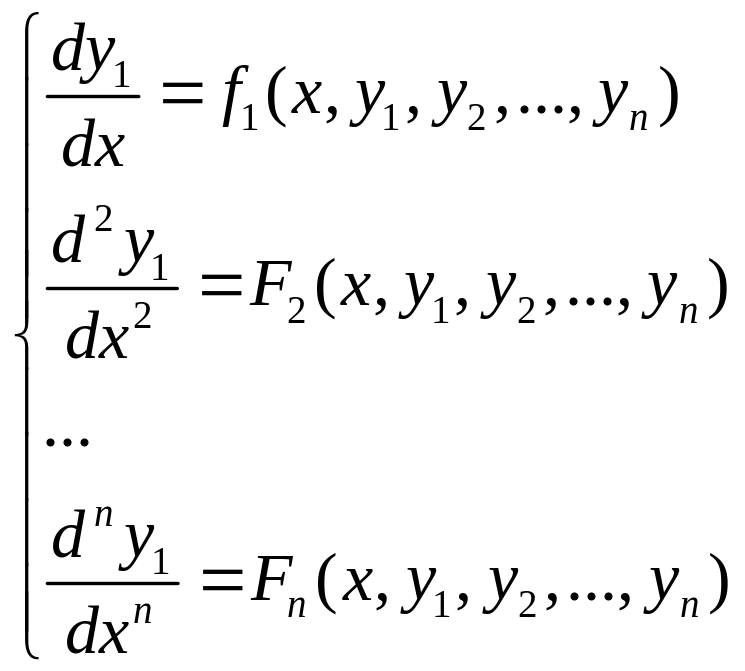Далее
из
уравнений определяем
,
,…
,
выразив их через
,
и производные
,
,…
(предполагая, что эти операции выполнимы)
.
Подставив
эти выражения в уравнение
,
получим уравнение n-го порядка для
определения
.
Если
исходная система дифференциальных
уравнений линейна относительно искомой
функции, то и выражение
будет линейным.
Решая
полученное уравнение, определим
:
.
Дифференцируя
это выражение
раз, найдем производные
,
,…
как функции от
,
,
,…
.
Подставляя эти функции в уравнения для
,
,…
получим
.
Для удовлетворения решения заданным начальным условиям необходимо найти значения постоянных , ,… .
Рассмотрим пример интегрирования следующей системы дифференциальных уравнений
при
начальных условиях
,
.
Дифференцируя по получим
.
Подставив
сюда выражения
и
из заданных уравнений, получим
или
.
Далее,
находим выражение
и подставляем его в только что полученное
уравнение, из чего получаем
или
.
Общее решение последнего уравнения есть
.
Для
удовлетворения начальных условий
необходимо чтобы
и
.
Отсюда
,
.
Таким образом, решения, удовлетворяющие
заданным начальным условиям, будут
иметь вид
,
.
В приведенных выше рассуждениях предполагалось, что из первых уравнений можно определить функции , ,… . Возможно, что переменные , ,… исключаются не из , а из меньшего числа уравнений. В этом случае получим уравнение, порядок которого ниже .