
- •Сокращения
- •Введение
- •1Виды сигналов и цепей
- •1.1Континуальные и дискретные сигналы
- •1.2Линейная цепь с постоянными параметрами
- •1.3Линейная цепь с переменными параметрами
- •1.4Нелинейная цепь
- •2Линейная фильтрация сигнала
- •2.1Классификация фильтров
- •2.2Частотные характеристики фильтров
- •2.3Фильтры второго порядка
- •Фильтры нижних частот
- •Фильтры верхних частот
- •Полосно-пропускающие фильтры
- •Частотно-заграждающие фильтры
- •Частотно-выделяющие фильтры
- •Всепропускающие фильтры
- •2.4Работа т-образного фильтра
- •3Цифровая обработка сигнала
- •3.1Структура цифровых ких и бих фильтров
- •3.2Интегрирование уравнений методом Эйлера
- •3.3Интегрирование уравнений методом Адамса
- •3.4Интегрирование системы уравнений
- •3.5Построение цифровых бих фильтров
- •4Аппаратные средства aTmega 8535 avr
- •4.1Функциональная схема архитектуры
- •4.2Специальные функции контроллера
- •4.3Основные характеристики периферии
- •4.4Память программ и данных
- •4.5Тактовый генератор и таймеры
- •4.6Периферийные устройства
- •4.7Модуль прерываний
- •4.8Порты контроллера
- •4.9Режимы пониженного энегопотребления
- •7.2Вторая часть задания
- •7.3Третья часть задания
- •Заключение Литература
- •Термины и определения
- •Линейные пространства
- •Дифференциальные уравнения
- •Комплексные числа
- •Гармонические функции
- •Законы Ома и Кирхгофа
- •Переходные процессы
- •Сигналы с ограниченной полосой частот
- •Средства пакета MathCad
- •Интерфейс MathCad
- •Построение выражений и их вычисление
- •Стандартные функции
- •Ввод греческих букв
- •Ввод текста
- •Варианты заданий
- •Пример выполнения задания
- •Частотные характеристики фильтра
- •Система дифференциальных уравнений
- •Составление системы уравнений
- •Решение системы средствами Odesolve
- •Система разностных уравнений
- •Решение системы разностных уравнений
- •Сравнение полученных решений
- •Дифференциальное уравнение 3-го порядка
- •Получение дифференциального уравнения
- •Сравнение частотных характеристик
- •Решение уравнения средствами Odesolve
- •Разностное уравнение
- •Решение разностного уравнения
- •Сравнение полученных решений
- •Программирование в среде Code Vision avr
- •Решение системы по разностной схеме
- •Результаты решения системы
- •Выводы по проделанной работе
7.2Вторая часть задания
ж) Используя составленную ранее систему дифференциальных уравнений, получить систему разностных уравнений.
з)
Построить графики решений системы
разностных уравнений
![]() ,
,
![]() ,
,
![]() ,
средствами пакета MathCAD
(при заданном числе шагов интегрирования
,
средствами пакета MathCAD
(при заданном числе шагов интегрирования
![]() и временном интервале
).
и временном интервале
).
и) Разработать и отладить программу (на языке С++), соответствующую полученной системе разностных уравнений средствами компилятора микропроцессорной системы (сконфигурировать микропроцессорную систему для работы с прерываниями, имеющими интервал времени ).
к) Построить графики решений разностных уравнений средствами симулятора микропроцессорной системы.
7.3Третья часть задания
Результаты выполнения заданий №1 и №2 представить преподавателю.
Заключение Литература
|
|
1. |
Атабеков Г.И. Основы теории цепей. Учебник для вузов . М., «Энергия», 1969 424с. |
2. |
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 600с. |
3. |
Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. – 4-е изд., перераб. и доп. – М.: Радио и связь, 1986. – 512с.: ил. |
4. |
Гребнев В.В. Микроконтроллеры семейства AVR фирмы Atmel. – М.: ИП РадиоСофт, 2002 – 176 с.: ил. |
5. |
Дмитрев Б.Ф., Красавчиков В.Г., Губанов Ю.А. Математические основы и практика применения символьного метода расчета электрических цепей: Учеб. пособие/СПб.,2004.111 с. |
6. |
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. Издательство «Наука», Главная редакция физико-математической литературы, М., 1972. |
7. |
Лебедев М.К. CodeVisionAVR Пособие для начинающих. – М.: Издательский дом «Додэка – XXI», 2008 – 592 с.: ил. |
8. |
Макаров Е.Г. Инженерные расчеты в MathCad. Учебный курс. – СПб.: Питер, 2003. – 448 с.: ил. |
9. |
Мошуц Г., Хорн П. Проектирование активных фильтров: Пер. с англ. – М.: Мир, 1984. – 320с., ил. |
10. |
Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов том 1 М., 1978г., 456 стр. с илл. |
11. |
Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов том 2 М., 1978г., 456 стр. с илл. |
12. |
Татур Т.А. Основы теории электрических цепей (справочное пособие): Учеб. пособие – М.: Высш. школа, 1980. _ 271с., ил. |
13. |
Шпак Ю.А. Программирование на языке Си для AVR и PIC микроконтроллеров. – М.: МК-Пресс, 2006 – 400 с.: ил. |
Термины и определения
Линейные пространства
Непустое множество элементов , , … называют линейным (или векторным) пространством, если оно удовлетворяет следующим условиям [ 9 ]:
а)
Для любых двух элементов
![]() однозначно определен третий элемент
однозначно определен третий элемент
![]() ,
называемый их суммой и обозначаемый
,
называемый их суммой и обозначаемый
![]() ,
причем:
,
причем:
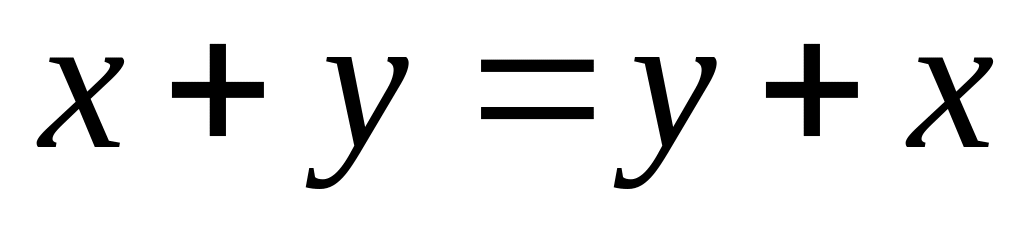 (коммутативность),
(коммутативность),
 (ассоциативность),
(ассоциативность),
в существует такой элемент
 ,
что
,
что
 для всех
для всех
 (существование нуля),
(существование нуля),
для каждого существует такой элемент
 ,
что
,
что
 (существование противоположного
элемента);
(существование противоположного
элемента);
б)
Для любого числа
![]() и любого элемента
определен элемент
и любого элемента
определен элемент
![]() (произведение числа
на элемент
),
причем:
(произведение числа
на элемент
),
причем:
 ,
,
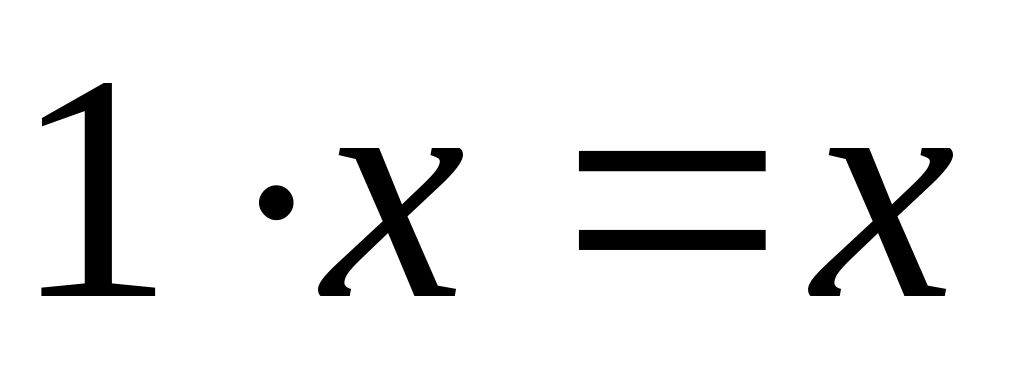 ,
,
 ,
,
 .
.
Элементы
,
,…
![]() линейного пространства
называют линейно зависимыми, если
существуют такие числа
,
линейного пространства
называют линейно зависимыми, если
существуют такие числа
,
![]() ,…
,…
![]() ,
не все равные
,
что
,
не все равные
,
что
![]() .
.
Числовую
функцию
![]() ,
определенную на некотором линейном
пространстве
,
называют функционалом.
,
определенную на некотором линейном
пространстве
,
называют функционалом.
Функционал называют аддитивным, если
![]() для
всех
,
для
всех
,
он называется однородным, если
![]() (
- произвольное число).
(
- произвольное число).
Функционал, обладающий свойством однородности, называют мультипликативным.
![]() .
.
Числовую
функцию
![]() ,
определенную на некотором линейном
пространстве
,
определенную на некотором линейном
пространстве
![]() ,
называют функционалом.
,
называют функционалом.
Функционал называют аддитивным, если
![]() для
всех
для
всех
![]() ,
,
он называется однородным, если
![]() (
(![]() - произвольное число).
- произвольное число).
Функционал, обладающий свойством однородности, называют мультипликативным.
