Обозначение шероховатости поверхности на чертежах

2.309-73 устанавливает обозначения и правила нанесения шероховатости поверхности на чертежах изделий.

Базовую длину для параметров Ra, Rz и R_max не указывают, если их числовые значения соответствуют значениям базовой длины.

Знаки шероховатости располагаются по линии контура детали на выносных линиях.

В тех случаях когда ко всем поверхностям детали устанавливаются одинаковые требования к шероховатости, эти требования указываются в правом верхнем углу чертежа детали.

Если поверхности детали по шероховатости нормируются в разной степени, то в правый верхний угол выносится наиболее часто повторяющееся требование: знак шероховатости и параметр шероховатости изображают увеличенным в 1,5 - 2 раза, а за ним в скобках помещают знак \/, который указывает на наличие поверхностей с иными показателями шероховатости, нанесенными непосредственно на изображение детали. Размеры и толщина линий знака в обозначении шероховатости должны быть приблизительно в 1,5 раза больше, чем в обозначениях, нанесенных на изображении.

Если среди обрабатываемых поверхностей по данному чертежу имеются поверхности без нормирования шероховатости, то выносить обозначения в угол чертежа не допускается.

Допускается применять упрощенное обозначение с разъяснением его в технических требованиях в случае неудобства размещения на поле чертежа.

22. Характеристика, область применения и расчет посадок с натягом, с зазором, переходных посадок.

Допуск посадки – сумма допусков отверстия и вала, составляющих соединение. Зазор – разность между размерами отверстия и вала до сборки, если размер отверстия больше размера вала. Натяг – разность между размерами вала и отверстия до сборки, если размер вала больше размера отверстия.

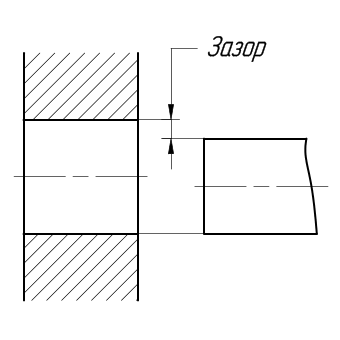
Посадка с зазором – посадка, при которой всегда образуется зазор в соединении, т.е. наименьший предельный размер отверстия больше наибольшего предельного размера вала или равен ему. При графическом изображении поле допуска отверстия расположено над полем допуска вала.

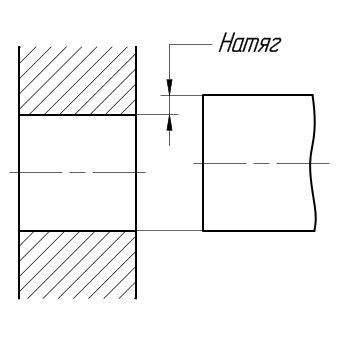
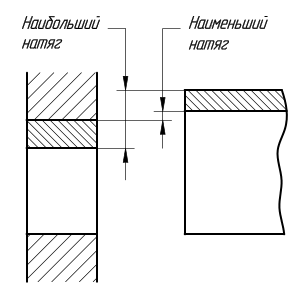
Посадка с натягом – посадка, при которой всегда образуется натяг в соединении, т.е. наибольший предельный размер отверстия меньше наименьшего предельного размера вала или равен ему. При графическом изображении поле допуска отверстия расположено под полем допуска вала.

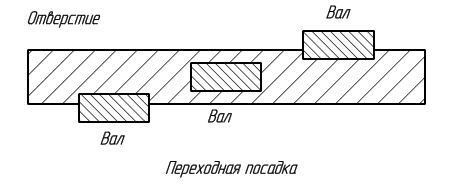
Переходная посадка – посадка, при которой возможно получение как зазора, так и натяга в соединении, в зависимости от действительных размеров отверстия и вала. При графическом изображении поля допусков отверстия и вала перекрываются полностью или частично.

Наименьший зазор – разность между наименьшим предельным размером отверстия и наибольшим предельным размером вала в посадке с зазором.

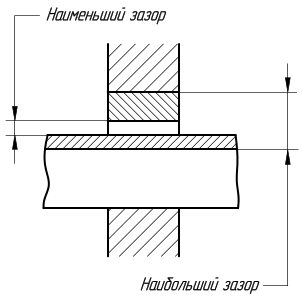
Наибольший зазор – разность между наибольшим предельным размером отверстия и наименьшим предельным размером вала в посадке с зазором или в переходной посадке.

Наименьший натяг – разность между наименьшим предельным размером вала и наибольшим предельным размером отверстия до сборки в посадке с натягом.

Наибольший натяг – разность между наибольшим предельным размером вала и наименьшим предельным размером отверстия до сборки в посадке с натягом или в переходной посадке.

Посадки в системе отверстия – посадки, в которых требуемые зазоры и натяги получаются сочетанием различных полей допусков валов с полем допуска основного отверстия.

Посадки в системе вала – посадки, в которых требуемые зазоры и натяги получаются сочетанием различных полей допусков отверстий с полем допуска основного вала.

23. Понятие о средствах измерений.

Средство измерений (СИ) – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее или хранящее единицу физической величины, размер которой принимают неизменной в течение известного интервала времени. Приведенное определение выражает суть средства измерений, которое, во-первых, хранит или воспроизводит единицу, во-вторых, эта единица неизменна. Эти важнейшие факторы и обуславливают возможность проведения измерений, т.е. делают техническое средство именно средством измерений. Этим средства измерений отличаются от других технических устройств. К средствам измерений относятся меры, измерительные: преобразователи, приборы, установки и системы. Мера физической величины – средство измерений, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью. Примеры мер: гири, измерительные резисторы, концевые меры длины, радионуклидные источники и др. Меры, воспроизводящие физические величины лишь одного размера, называются однозначными (гиря), нескольких размеров – многозначные (миллиметровая линейка – позволяет выражать длину как в мм, так и в см). Кроме того, существуют наборы и магазины мер, например, магазин емкостей или индуктивностей. При измерениях с использованием мер сравнивают измеряемые величины с известными величинами, воспроизво-димыми мерами. Сравнение осуществляется разными путями, наиболее распространенным средством сравнения являетсякомпаратор, предназначенный для сличения мер однородных величин. Примером компаратора являются рычажные весы. К мерам относятся стандартные образцы и образцовое вещество, которые представляют собой специально оформленные тела или пробы вещества определенного и строго регламентированного содержания, одно из свойств которых является величиной с известным значением. Например, образцы твердости, шероховатости.  Измерительный преобразователь (ИП) - техническое средство с нормативными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, индикации или передачи. Измерительная информация на выходе ИП, как правило, недоступна для непосредственного восприятия наблюдателем. Хотя ИП являются конструктивно обособленными элементами, они чаще всего входят в качестве составных частей в более сложные измерительные приборы или установки и самостоятельного значения при проведении измерений не имеют. Преобразуемая величина, поступающая на измерительный преобразователь, называется входной, а результат преобразования – выходной величиной. Соотношение между ними задается функцией преобразования, которая является его основной метрологической характеристикой.  Для непосредственного воспроизведения измеряемой величины служат первичные преобразователи, на которые непосредственно воздействует измеряемая величина и в которых происходит трансформация измеряемой величины для ее дальнейшего преобразования или индикации. Примером первичного преобразователя является термопара в цепи термоэлектрического термометра. Одним из видов первичного преобразователя является датчик – конструктивно обособленный первичный преобразователь, от которого поступают измерительные сигналы (он «дает» информацию). Датчик может быть вынесен на значительное расстояние от средства измерений, принимающего его сигналы. Например, датчик метеорологического зонда. В области измерений ионизирующих излучений датчиком часто называют детектор.  По характеру преобразования ИП могут быть аналоговыми, аналого-цифровыми (АЦП), цифро-аналоговыми (ЦАП), то есть, преобразующими цифровой сигнал в аналоговый или наоборот. При аналоговой форме представления сигнал может принимать непрерывное множество значений, то есть, он является непрерывной функцией измеряемой величины. В цифровой (дискретной) форме он представляется в виде цифровых групп или чисел. Приме-рами ИП являются измерительный трансформатор тока, термометры сопротивлений. Измерительный прибор – средство измерений, предназна-ченное для получения значений измеряемой физической величины в установленном диапазоне. Измерительный прибор представляет измерительную информацию в форме, доступной для непосредственного восприятия наблюдателем.  По способу индикации различают показывающие и регистрирующие приборы. Регистрация может осуществляться в виде непрерывной записи измеряемой величины или путем печатания показаний прибора в цифровой форме.  Приборы прямого действия отображают измеряемую величину на показывающем устройстве, имеющем градуировку в единицах этой величины. Например, амперметры, термометры. Приборы сравнения предназначены для сравнения измеряемых величин с величинами, значения которых известны. Такие приборы используются для измерений с большей точностью.  По действию измерительные приборы разделяют на интегрирующие и суммирующие, аналоговые и цифровые, самопишущие и печатающие. Измерительная установка и система – совокупность функционально объединенных мер, измерительных приборов и других устройств, предназначенных для измерений одной или нескольких величин и расположенная в одном месте (установка) или в разных местах объекта измерений (система). Измерительные системы, как правило, являютсяавтоматизированными и по существу они обеспечивают автоматизацию процессов измерения, обработки и представления результатов измерений. Примером измерительных систем являются автоматизированные системы радиационного контроля (АСРК) на различных ядерно-физических установках, таких, например, как ядерные реакторы или ускорители заряженных частиц. По метрологическому назначению средства измерений делятся на рабочие и эталоны.  Рабочее СИ - средство измерений, предназначенное для измерений, не связанное с передачей размера единицы другим средствам измерений. Рабочее средство измерений может использоваться и в качестве индикатора. Индикатор – техническое средство или вещество, предназначенное для установления наличия какой-либо физической величины или превышения уровня ее порогового значения. Индикатор не имеет нормированных метрологических характеристик. Примерами индикаторов являются осциллограф, лакмусовая бумага и т.д.  Эталон - средство измерений, предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера другим средствам измерений. Среди них можно выделить рабочие эталоны разных разрядов, которые ранее назывались образцовыми средствами измерений. Классификация средств измерений проводится и по другим различным признакам. Например, по видам измеряемых величин, по виду шкалы (с равномерной или неравномерной шкалой), по связи с объектом измерения (контактные или бесконтактные).

24. Метрологические характеристики средств измерений. Классы точности.

Метрологическими характеристиками, согласно ГОСТ 8.009-84, называются технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, предназначенные для оценки технического уровня и качества средства измерений, для определения результатов измерений и расчетной оценки характеристик инструментальной составляющей погрешности измерений.

Характеристики, устанавливаемые нормативно-техническими документами, называются нормируемыми, а определяемые экспериментально — действительными.

Ниже приведена номенклатура метрологических характеристик:

• Характеристики, предназначенные для определения результатов измерений (без введения поправок):

- Функция преобразования измерительного преобразователя, а также измерительного прибора с неименованной шкалой; - Значение однозначной меры; - Цена деления шкалы измерительного прибора или многозначной меры; - Вид выходного кода для цифровых средств измерений;

• Характеристики погрешностей средств измерений;

• Характеристики чувствительности средств измерений к влияющим величинам;

• Динамические погрешности средств измерений (переходная характеристика, АЧХ, АФХ и т.д.).

Класс точности средств измерений - обобщенная характеристика средств измерений, определяемые пределами допускаемых основной и дополнительной погрешностей, а также другими свойствами средств измерений, влияющими на их точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений. Классы точности присваиваются средствам измерений при их разработке с учетом результатов государственных приемочных испытаний. Класс точности хотя и характеризует совокупность метрологических свойств данного средства измерений, однако не определяет однозначно точность измерений, так как последняя зависит от метода измерений и условий их выполнения.

Средствам измерений с двумя или более диапазонами измерений одной и той же физической величены допускается присваивать два или более класса точности. Средствам измерений, предназначенным для измерений двух или более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины. С целью ограничения номенклатуры средтсв измерений по точности для СИ конкретного вида устанавливают ограниченное число классов точности, определяемое технико-экономическими обоснованиями.

Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для дополнительной обработки результатов измерений устанавливают без учета режима обработки.

Способы нормирования и формы выражения метрологических характеристик

Пределы допускаемых основной и дополнительных погрешностей следует выражать в форме приведенных, относительных или абсолютных погрешностей в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений конкретного вида. Пределы допускаемой дополнительной погрешности допускается выражать в форме, отличной от формы выражения пределов допускаемой основной погрешности.

Пределы допускаемой основной погрешности устанавливают в последовательности, приведенной ниже:

• Устанавливаются пределы допускаемой абсолютной погрешности по формуле: 

Δ = ± а

или 

Δ = ± (а + b·x) 

где Δ - пределы допускаемой абсолютной основной погрешности (в единицах измеряемой величины или условно в делениях шкалы) х - значение измеряемой величины, а, b - положительные числа, не зависящие от х.

• Устанавливаются пределы допускаемой приведенной основной погрешности по формуле: 

 γ = Δ / Хn = ± p 

где γ - пределы допускаемой приведенной основной погрешности в %, Δ - пределы допускаемой абсолютной погрешности, p - положительное число, выбираемое из ряда 1·10ⁿ, 1,5·10ⁿ, (1,6·10ⁿ)*, 2·10ⁿ,  2,5·10ⁿ, (3·10ⁿ)*, 4·10ⁿ, 5·10ⁿ, 6·10ⁿ (n = 1, 0, -1, -2 и т.д.) *не устанавливается для вновь разрабатываемых средств измерений, для средств измерений конкретного типа допускается устанавливать не более пяти различных пределов допускаемой основной погрешности при одном и том же значении степени n.

• Устанавливается нормируещее занчение Хn

• Для средств измерений с равномерной, практически равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение измеряемого параметра находся на краю или вне диапазона измерений нормирующее значение устанавливается равным большему из пределов измерений. Для средств измерений, нулевое значение измеряемого параметра которых находится внутри диапазона измерений, нормирующее значение устанавливается раным большему из модулей пределов измерений.

• Для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений нормирующее значение допускается устанавливать равным сумме модулей пределов измерений.

• Для средств измерений физической величины, для которых принята шкала с условным нулем, нормирующее значение устанавливают равным модулю разности пределов измереинй.

• Для средств измерений с установленным номинальным значением нормирующее значение устанавливают равным этому номинальному значению.

• Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным всей длине шкалы или её части, соответствующей диапазону измерений. В этом случае пределы абсолюной погрешности выражают, как и длину шкалы, в единицах длины.

• Устанавливаются пределы допускаемой относительной основной погрешности по формуле: 

δ = Δ / х = ± [c + d·(|х_к / х| - 1)] =<  ± q

где с = b + d;  d = a / |х_к| δ - пределы допускаемой относительной основной погрешности в %, Δ - пределы допускаемой абсолютной основной погрешности (в единицах измеряемой величины или условно в делениях шкалы) х - значение измеряемой величины, х_к - наибольший (по модулю) из пределов измерений, а, b - положительные числа, не зависящие от х. q, c, d - положительное число, выбираемое из ряда 1·10ⁿ, 1,5·10ⁿ, (1,6·10ⁿ)*, 2·10ⁿ,  2,5·10ⁿ, (3·10ⁿ)*, 4·10ⁿ, 5·10ⁿ, 6·10ⁿ (n = 1, 0, -1, -2 и т.д.) *не устанавливается для вновь разрабатываемых средств измерений, для средств измерений конкретного типа допускается устанавливать не более пяти различных пределов допускаемой основной погрешности при одном и том же значении степени n. В обоснованных случаях пределы допускаемой относительной оснвоной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы. В стандартах или технических условиях на средтсва измерений должно быть установлено минимальное значение х, начиная от которого применим принятый способ выражения пределов допускаемой относительной погрешности. Соотношение между числами с и d устанавливаются в стандартах на средства измерений конкретного вида.

• Пределы допускаемых дополнительных погрешностей устанавливают одним из следующих способов:

  • в виде постоянного значения для всей рабочей области влияю-щей величины или в виде постоянных значений по интервалам рабочей области влияющей величины;

  • путем указания отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;

  • путем указания зависимости предела допускаемой дополнительной погрешности от влияющей величины (предельной функции влияния);

  • путем указания функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.

• Для различных условий эксплуатации средств измерений в рамках одного и того же класса точности допускается устанавливать различные рабочие области влияющих величин. Предел допускаемой вариации выходного сигнала следует устанавливать в виде дольного (кратного) значения предела допускаемой основной погрешности или в делениях шкалы. Пределы допускаемой нестабильности, как правило, устанавливают в виде доли предела допускаемой основной погрешности. Пределы допускаемых погрешностей должны быть выражены не более чем двумя значащими цифрами, причем погрешность округления при вычислении пределов должна быть не более 5%.

Обозначение классов точности средств измерений в документации

• Для средств измерений пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей или относительных погрешностей, причем последние установлены в виде графика, таблицы или формулы, классы точности в документации обозначаются прописными буквами латинского алфавита или римскими цифрами.

• В необходимых случаях к обозначению класса точности буквами латинского алфавита добавляют индексы в виде арабской цифры. Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, соответствуют буквы, находящиеся ближе к началу алфавита, или цифры, означающие меньшие числа.

• Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме приведенной погрешности или относительной погрешности в соответствии с формулой δ = Δ / х  =  ± q, классы точности в документации следует обозначаются числами, которые равны этим пределам погрешности, выраженными в процентах. Обозначение класса точности таким образом, дает непосредственное указание на предел допускаемой основной погрешности.

• Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей в соответствии с формулой δ = ± [c + d·(|х_к / х| - 1)], классы точности в документации обозначаются числами с и d, разделенных косой чертой.

В документации на средства измерений допускается обозначать классы точности так же, как на средтсвах измерений. В эксплуатационной документации на средство измерений конкретного вида, содержащей обозначение класса точности, содержится ссылка на стандарт или технические условия, в которых установлен класс точности этого средства измерений.

Обозначение классов точности на средствах измерений

Условные обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений. При указании классов точности на измерительных приборах с существенно неравномерной шкалой, для информации, дополнительно указываются пределы допускаемой основной относительной погрешности для части шкалы, лежащей в пределах, отмеченных специальными знаками (например точками или треугольниками). К значению предела допускаемой относительной погрешности в этом случае добавляют знак процента и помещают в кружок. Обращаем ваше внимание на то, что этот знак не является обозначением класса точности. Обозначение класса точности допускается не наносить на высокоточные меры, а также на средства измерений, для которых действующими стандартами установлены особые внешние признаки, зависящие от класса точности, например параллелепипедная и шестигранная форма гирь общего назначения. За исключением технически обоснованных случаев, вместе с условным обозначением класса точности на циферблат, щиток или корпус средств измерений наносится обозначение стандарта или технических условий, устанавливающих технические требования к этим средствам измерений. На средства измерений, для одного и того же класса точности которых в зависимости от условий эксплуатации установлены различные рабочие области влияющих величин, наносятся обозначения условий их эксплуатации, предусмотренные в стандартах или технических условиях на эти средства измерений.

Расшифровка обозначений классов точности на средствах измерений

Обозначение класса точности		Форма выражения погрешности	Пределы допускаемой основной погрешности	Примечание
на средстве измерений	в документации
0,5	Класс точности 0,5	Приведенная	γ = ±0,5%	нормирующее значение выражено в единицах измеряемой величины
	Класс точности 0,5		γ = ±0,5%	нормирующее значение принято равным длине шкалы или её части
	Класс точности 0,5	Относительная	δ = ±0,5%	δ = Δ / х
0,02/0,01	Класс точности 0,02/0,01		δ = ±[0,02 + 0,01·(|хк / х| - 1)] %	δ = ±[c + d·(|хк / х| - 1)]

 

25. Понятие об измерении по шкале отношений.

25 Шкалы измерений В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений ипроцессов. Разнообразные проявления (качественные или количественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае, условных знаков, образуют шкалы измерения этих свойств. Шкала физической величины - это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений. Термины и определения теории шкал измерений изложены в документе МИ 2365-96. Различают пять основных типов шкал измерений. 1. Шкала наименований (шкала классификации). Самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имён.  Нумерация объектов по шкале наименований осуществляется по принципу: "не приписывай одну и ту же цифру разным объектам".  Числа, приписанные объектам, нельзя использовать для суммирования и других математических операций. В этих шкалах отсутствует понятие нуля, "больше" или "меньше" и единицы измерения. Примером шкал наименований являются атласы цветов, предназначенные для идентификации цвета. Естественнее всего использовать шкалу наименований в тех случаях, когда классифицируются дискретные по своей природе явления (например, различные объекты). Для обозначения классов могут быть использованы как символы естественного языка (географические названия), произвольные символы (флаги, значки), номера (на майках спортсменов), так и их различные комбинации. Все эти обозначения эквивалентны простой нумерации. Необходимость классификации возникает и в тех случаях, когда классифицируемые состояния образуют непрерывное множество. Задача сводится к предыдущей, если все множество разбить на конечное число подмножеств, искусственно образуя тем самым классы эквивалентности. Однако эквивалентность внутри класса носит условный характер. Подчеркнем еще раз, что обозначения классов - это только символы, даже если для этого использованы номера. Номера лишь внешне выглядят как числа, но на самом деле числами не являются. Поэтому при обработке экспериментальных данных, зафиксированных в номинальной шкале, непосредственно с самими данными можно выполнять только операцию проверки их совпадения или несовпадения.

26. Основной постулат метрологии.

Любое измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражение первого через второе в кратном или дольном отношении.

Главной особенностью измерительной процедуры является то, что при ее повторении отсчет каждый раз получается разным. На основании громадного опыта практических измерений, накопленного к настоящему времени, может быть сформулировано следующее утверждение, называемое основным постулатом метрологии: отсчет является случайным числом. На этом постулате, который легко поддается проверке и остается справедливым в любых областях и видах измерений, основана вся метрология.

Для изучения свойств случайных событий в больших объемах используют аппарат теории вероятностей и математической статистики. При этом рассматривается появление случайных погрешностей как случайных событий при многократно повторяемых наблюдениях.

Для дальнейшего рассмотрения теории случайных погрешностей кратко приведем основные термины и понятия теории вероятностей и математической статистики.

В теории вероятностей случайным называется такое событие, которое может произойти или не произойти при осуществлении определенного комплекса условий. Для измерений это понятие можно трансформировать так, что при повторных наблюдениях в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результата может или появиться, или нет.

Если обозначить истинное значение измеряемой величины через а, то можно написать следующее равенство:

,

где   i – номер наблюдения, х_i – результат наблюдения; d_i – случайная погрешность.

Вероятность наступления события А есть отношение числа появлений события А (m) к общему числу событий (n):

.

Вероятность является численной оценкой объективной возможности появления события. Вероятность достоверного события = 1, а вероятность невозможного события = 0.

Определение вероятности подсчетом оказывается крайне затруднительным в определенных случаях. Обычно применяется статистический метод определения вероятности события, который опирается на то, что в результате длительных наблюдений явлений массового характера, было установлено, что то или иное событие сохраняет устойчивую частоту появления по отношению к общему числу всех рассматриваемых событий. Я. Бернулли доказал, что при неограниченном увеличении числа однородных независимых опытов можно утверждать, что частота появлений событий будет сколь угодно мало отличаться от их вероятности.

27. Закономерности формирования результата измерения.