Двойственные функции

Функция g(x₁,...,x_n) = ¬f(¬x₁,...,¬x_n) называется двойственной функцией к функции f и обозначается f^* .

Пример (x & y)^* = ¬(¬x & ¬y) = x  y.

Теорема: Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f^*(x₁,...,x_n)^* = (¬f(¬x₁,...,¬x_n))^* = ¬¬f(¬¬x₁,...,¬¬x_n) = f(x₁,...,x_n)

Рассмотрим, что происходит с таблицей двойственной функции. Замена набора (x₁,...,x_n) на (¬x₁,...,¬x_n) соответствует ``переворачиванию'' таблицы. Действительно, наборы (x₁,...,x_n) и (¬x₁,..., ¬x_n) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию ¬ к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Функции x & y и x  y, задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являются x  y и x  y, задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функций x и ¬x (векторы (0,1) и (1,0) соответственно) двойственна сама себе.

Принцип двойственности.

Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее:

f₀(f₁,...,f_m)^* = f₀^*(f₁^*,...,f_m^*)

Полные системы функций (связок).

Система функций является полной, если любая n-арная булева функция может быть записана в виде пропозициональной формулы с использованием только функций входящих в эту систему.

Система {¬,∨,∧,→,↔} является полной.

Система {¬,∨,∧} является полной. Именно она и составляет сигнатуру Булевой Алгебры.

Системы {¬,→}, {|} (штрих шеффера), так же полны.

Вторая система – только И-НЕ является важной для микроэлектроники.

Последняя система позволяет представить булевы функции в виде полиномов (полиномов Жигалкина)

Замкнутый класс – это такое множество функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: [P] = P (то есть, любая функция, которую можно записать с помощью только функций входящих в P так же входит в P).

критерий Поста: Система булевых функций является полной тогда и только тогда, когда он не содержится целиком ни в одном из пяти замкнутых классов:

• монотонные функции

}

• функции, сохраняющие нуль

• функции, сохраняющие единицу

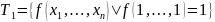
• линейные функции

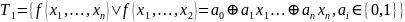
• самодвойственные функции

Если функции содержатся в одном из классов, то и все композиции также не выходят за пределы этого класса (легко проверить для каждого из классов в отдельности) и поэтому система не является полной.

Можно показать, что имея функции по крайней мере из 2 разных классов, можно выразить любую другую функцию. (http://www.intuit.ru/department/calculate/lancalc/1/3.html)

Дизъюнктивные и конъюнктивные нормальные формы.

Элементарной конъюнкцией называется конъюнкция переменных высказываний и (или) их отрицаний.

Например:

Элементарной дизъюнкцией называется дизъюнкция переменных высказываний и (или) их отрицаний.

Например:

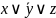
Введём обозначение .

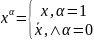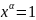тогда и только тогда, если .

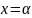Это позволяет записать элементарные конъюнкции 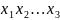в виде (точнее 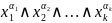, но знак конъюнкции обычно опускают), где в качестве значений 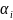берётся 0 если 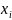входит в конъюнкцию с отрицанием, и 1 если без отрицания. Так же, элементарные дизъюнкции могут быть записаны в виде .

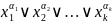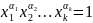1. тогда и только тогда, если

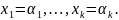
Элементарная конъюнкция даёт 1 только на наборе переменных, в котором переменные, входящие в неё с отрицанием имеют значение 0, а переменные без отрицания 1.

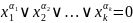2. тогда и только тогда, если

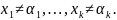
Элементарная дизъюнкция даёт 0 только на наборе переменных, в котором переменные, входящие в неё с отрицанием имеют значение 1, а переменные без отрицания 0)

Дизъюнктивной нормальной формой (ДНФ) данной формулы называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Например, выражение 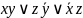является ДНФ.

Конъюнктивной нормальной формой (КНФ) данной формулы называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Например, выражение – КНФ.

Для того, чтобы построить по данной формуле алгебры логики равносильную ей ДНФ или КНФ необходимо:

1. Перейти в сигнатуру алгебры логики (выразить все операции через дизъюнкцию, конъюнкцию и отрицание),

2. Воспользоваться законом де Моргана для того, чтобы отрицания стояли лишь над элементарными переменными высказываниями,

3. Раскрыть скобки (для построения ДНФ) или воспользоваться дистрибутивным законом (для построения КНФ).