Алгебра логики (булева алгебра).

Алгебра логики. Функции алгебры логики. Таблицы истинности. Пропозициональные формулы. Равносильные формулы. Основные тождества алгебры логики. Двойственные функции. Полные системы связок. Конъюнктивные и дизъюнктивные нормальные формы. Совершенные КНФ и ДНФ. Тавтологии. Противоречия. Проблема разрешимости в алгебре логики. Логические следствия. Основные схемы доказательств.

Алгебра логики

Алгебраическая система (алгебра) – пара <G, M>, где G - это множество элементов (носитель), а M – множество операций, заданных на G (сигнатура).

(n-арная операция на G задаёт отображение 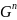на G)

Определение: Алгебраическая система, образованная множеством B = {0,1} вместе со всеми возможными операциями на нем, называется алгеброй логики.

Функцией алгебры логики (или логической функцией) от n переменных называется n-арная операция на В. Эта функция может принимать значения 0 или 1. (т.о. задаёт отображение B^n -> B)

Чаще всего под алгеброй логики понимают алгебру, сигнатура которой включает 3 операции: отрицание, конъюнкцию и дизъюнкцию.

Основные функции алгебры логики:

x1	u1	u2	u3	u4
0	0	0	1	1
1	0	1	0	1

Унарные:

Всего теоретически возможны 4 унарных операции, но лишь одна из них имеет собственное название и обозначение.

u3 - Отрицание: 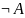(читается: не-А)

Бинарные:

Всего существует 16 бинарных функций алгебры логики:

x1	x2	b1	b2	b3	b4	b5	b6	b7	b8	b9	b10	b11	b12	b13	b14	b15	b16
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

b2 - Конъюнкция: (читается А и В)

b8 - Дизъюнкция: 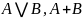(А или В)

b12 - Импликация: (из А следует В)

Результат импликации ложен только тогда, когда исходное (А) высказывание ложно, а результат (B) истинен.

Примеры: (x делится на 4) -> (x делится на 2), Если 2*2 = 5 то 2*2 = 4

b10 - Эквиваленция: 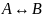, (А равносильно В)

Результат эквиваленции есть истина, если A и B одновременно истины либо ложны (Иными словами, если A=B)

b7 – сложение по модулю или неравнозначность, x1x2

Результат сложения по модулю истинен, если истинно лишь одно из A и B (То есть, если A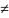 B)

b9 – cтрелка Пирса x1x2 («или-не»). Результат этой операции равносилен последовательному применению операций дизъюнкции и отрицания

b15 – штрих Шеффера обозначается x1x2, «и-не». Результат этой операции равносилен последовательному применению операций конъюнкции и отрицания. Соответственно, результирующее высказывание будет ложным, только если входящие в него высказывания одновременно истинны. Штрих Шеффера - это операция замечательная тем, что её одной (необходимое количество раз применённой) достаточно, чтобы записать любое сложное высказывание. Является основной операцией в электронике.