13. Математическая статистика.

1. Численная обработка данных одномерной выборки.

Выборка X объемом N = 100 измерений задана таблицей:

где х , — результаты измерений, — частоты, с которыми встречаются значения:

По параметрам m=3, n=3 выборка X объемом N = 100 измерений получится в виде таблицы, где рассчитаны по формуле:

,

где

Задача 13.1.1.

Построить полигон относительных частот .

Решение:

Вычислим по формуле относительные частоты:

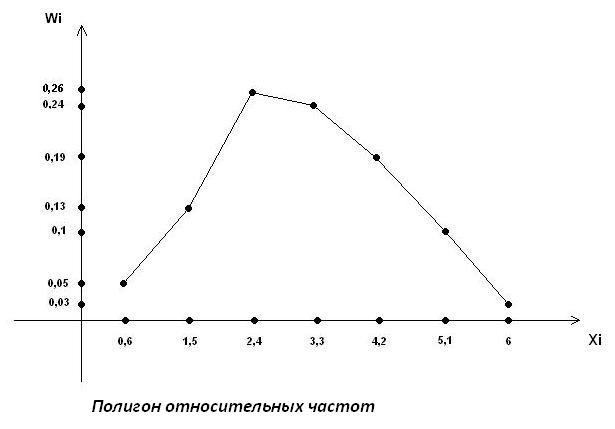
(полигон получен соединением отрезками ломаной точек с координатами: ( , )) .

Задача 13.1.2.

Вычислить среднее выборочное , выборочную дисперсию и среднее квадратическое отклонение .

Примечание. Для расчетов и рекомендуется перейти к условным значениям , взяв за ложный нуль значение c наибольшей частотой; использовать суммы:

и .

Решение:

Вычислим среднее выборочное , выборочную дисперсию и среднее квадратическое отклонение .

Взяв за ложный нуль , переходим к условным значениям (выбрано с наибольшей частотой )

(в знаменателе определено в примечании)

Распределение условных вариант (значений):

Вычислим:

По формуле ,

получим средняя выборочная

Вычислим:

По формуле:

вычислим:

выборочная дисперсия.

Так как , то ,

значит среднее квадратическое отклонение.

Задача 13.1.3.

По критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости

Решение:

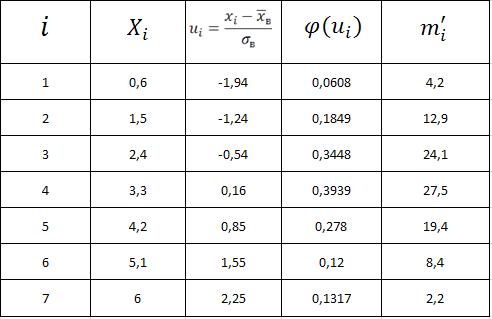
Составим расчетную таблицу. Значения получены из таблицы значений функции Гаусса ;

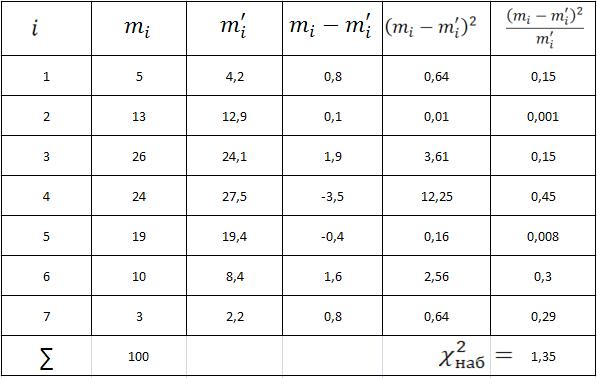
Сравним эмпирические и теоретические частоты с помощью критерия Пирсона ( критерий). Составим расчетную таблицу, из которой найдем наблюдаемые значения критерия:

По таблице критических точек распределения по уровню значимости и числу степеней свободы находим критическую точку правосторонней критической области . Так как нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, то есть эмпирические и теоретические частоты различаются незначимо (случайно).

ЛИТЕРАТУРА