
- •Основные теоретические сведения для выполнения
- •Приложения производной к задачам геометрии.
- •Полное исследование функций и построение графика.
- •Функции нескольких переменных и их дифференцирование.
- •Полный дифференциал функции двух переменных и его применение в приближенных вычислениях.
- •Решение типового варианта (задания 1-9).
- •1)Hайти пределы функций, пользуясь правилом Лопиталя (для случаев, когда оно применимо).
- •3)Найти первую производную неявной функции и функции, заданной параметрически.
- •5).Сделать разложение функции по формуле Тейлора при указанном значении :
- •6. Составить уравнение касательной и нормали к кривой в точке .
- •8. Дана функция . Показать, что .
- •9. Дана функция и точка . С помощью дифференциала вычислить приближенное значение функции в данной точке..
Решение типового варианта (задания 1-9).
1)Hайти пределы функций, пользуясь правилом Лопиталя (для случаев, когда оно применимо).
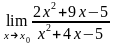 при
при
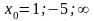 ;
;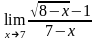 ;
; ;
;
Найдём
пределы, используя правило Лопиталя,
которое применимо при неопределённостях
вида
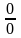 и
и
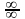 .Это
условие выполняется для 2) и 3) примеров
и для 1) примера при
.Это
условие выполняется для 2) и 3) примеров
и для 1) примера при
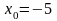 и
и
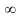 .
.
Пусть :

Пусть
 :
:

2)
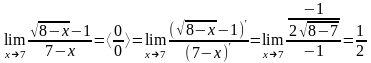
3)

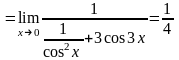 .
.
2)Найти производные функций, заданных в явном виде .
а)
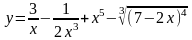
Запишем у(х) в виде, удобном для дифференцирования;
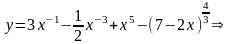
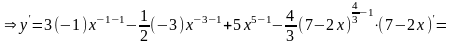

б)
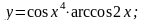
Используем формулу для производной произведения функций:
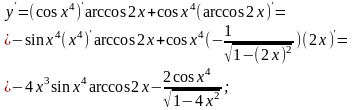
в)
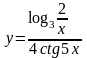 .
.
Используем формулу для производной частного двух функций (константа 4 в знаменателе при этом выносится из под дифференцирования ) :
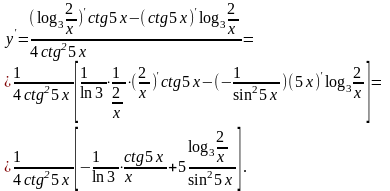
г)
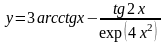 ,
,
перепишем 2-е слагаемое в виде, удобном для дифференцирования, после чего для него используем формулу для производной произведения двух функций:
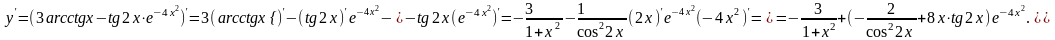
д)
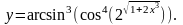
Дифференцируем по правилу производной сложной функции. Введем обозначения, которые каждую фигурирующую в выражении функцию сводят к простейшей :
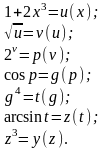
З
аписываем формулу дифференцирования сложной функции в буквенном виде, а затем расписываем производные и переходим к первоначальной производной по х:
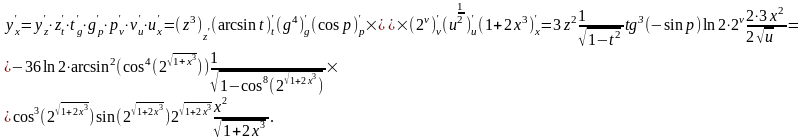
e)
 .
.
Логарифмируем обе части равенства, после чего дифференцируем полученное равенство:

Отсюда
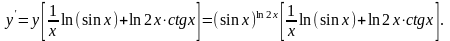
3)Найти первую производную неявной функции и функции, заданной параметрически.
а)
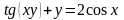 ;
б)
;
б)
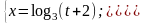
Решение.
a) Считая функцией от , дифференцируем обе части равенства по :
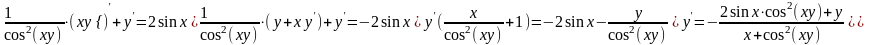
б)
Используем формулу (7) для
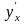 при параметрическом дифференцировании:
при параметрическом дифференцировании:
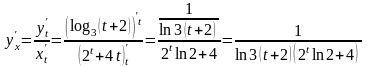 .
.
4).Найти
наименьшее и наибольшее значение функции
 на отрезке
на отрезке
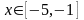 .
.
Найдем критические точки из условия равенства нулю 1-ой производной :
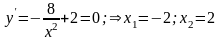 .
.
Так
как
,
то эту критическую точку не учитываем.
Чтобы выяснить, имеет ли функция экстремум
в точке
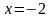 ,
найдём
,
найдём
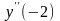 :
:
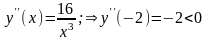 ,
,
т.е.
в точке
функция имеет максимум. Находим значения
функции в точках
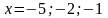 :
:
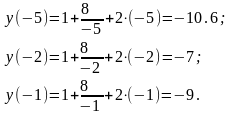
Т.е.
минимальное значение
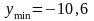 функция принимает на левом конце
отрезка, а максимальное
функция принимает на левом конце
отрезка, а максимальное
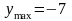 внутри отрезка при
.
внутри отрезка при
.
5).Сделать разложение функции по формуле Тейлора при указанном значении :
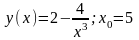 .
.
Находим производные и подметив закономерность, запишем выражение для n-ой производной
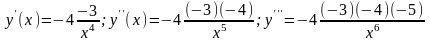 .
.
Легко заметить ,что n-я производная будет равна
 .
.
Умножив
числитель и знаменатель на (-1)(-2),
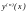 запишется в виде:
запишется в виде:
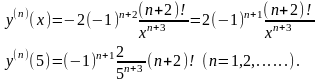
Используя формулу (8) получим:

6. Составить уравнение касательной и нормали к кривой в точке .
Решение: Найдем сначала
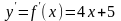 ,
,
подставляя координату точки , получаем
 .
.
Подставляя в формулу (2), находим уравнение касательной
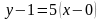 или
или
 .
.
Подставляя в формулу (3), выводим уравнение нормали
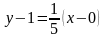 или
или
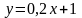 .
.
Тангенс
угла, образованного касательной с осью
абсцисс, равен
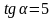 ,
откуда
,
откуда
 .
.
Ответ: уравнение касательной ; нормали ; угол .
7.
Провести полное исследование
функции
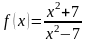 и построить ее график.
и построить ее график.
Решение.
1). Область определения функции.
Очевидно,
что эта функция определена на всей
числовой прямой, кроме точек “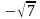 ”
и “
”
и “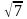 ”,
т.к. в этих точках знаменатель равняется
нулю и, следовательно, функция не
существует, а прямые
”,
т.к. в этих точках знаменатель равняется
нулю и, следовательно, функция не
существует, а прямые
 и
и
 – вертикальные асимптоты.
– вертикальные асимптоты.
2). Поведение функции при стремлении аргумента к бесконечности, существование точек разрыва и проверка наличия наклонных асимптот.
Проверим сначала как ведет себя функция при приближении к бесконечности влево и вправо.
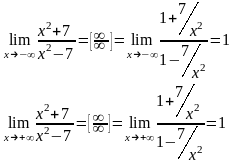
Таким
образом, при
 функция стремится к 1, т.е.
функция стремится к 1, т.е.
 – горизонтальная асимптота.
– горизонтальная асимптота.
В окрестности точек разрыва поведение функции определяется следующим образом:
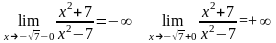
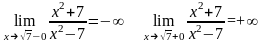
Т.е. при приближении к точкам разрыва слева функция бесконечно убывает, справа – бесконечно возрастает.
Наличие наклонной асимптоты определим, рассмотрев равенство:
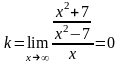 .
.
Наклонных асимптот нет.
3). Точки пересечения с осями координат.
Здесь необходимо рассмотреть две ситуации: найти точку пересечения с осью Ох и с осью Оу. Признаком пересечения с осью Ох является нулевое значение функции, т.е. необходимо решить уравнение:
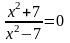
Это уравнение не имеет корней, следовательно, точек пересечения с осью Ох у графика данной функции нет.
Признаком пересечения с осью Оу является значение х = 0. При этом
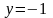 ,
,
т.е.
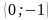 – точка пересечения графика функции с
осью Оу.
– точка пересечения графика функции с
осью Оу.
4). Определение точек экстремума и промежутков возрастания и убывания.
Для исследования этого вопроса определим первую производную:
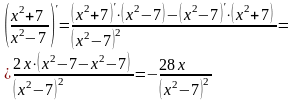 .
.
Приравняем к нулю значение первой производной.
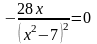 .
.
Дробь равна нулю, когда равен нулю ее числитель, т.е.
.
Определим промежутки возрастания и убывания функции.
Таблица 5

Т.о., функция имеет одну точку экстремума и в двух точках не существует.
Таким
образом, функция возрастает на промежутках
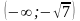 и
и
 и убывает на промежутках
и убывает на промежутках
 и
и
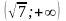 .
.
Как
видно из таблицы 5,
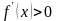 при
при
 и
и
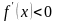 при
при
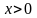 ,
т.е. при
функция имеет максимум.
,
т.е. при
функция имеет максимум.
5). Точки перегиба и участки выпуклости и вогнутости.
Эта характеристика поведения функции определяется с помощью второй производной. Определим сначала наличие точек перегиба. Вторая производная функции равна
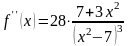 .
.
Таблица 6

При
 и функция вогнута; при
и функция вогнута; при

 и функция выпуклая.
и функция выпуклая.
6). Построение графика функции.
Используя в пунктах найденные величины, построим схематически график функции:
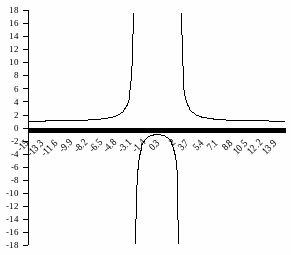
Рис.5
