
- •Основные теоретические сведения для выполнения
- •Приложения производной к задачам геометрии.
- •Полное исследование функций и построение графика.
- •Функции нескольких переменных и их дифференцирование.
- •Полный дифференциал функции двух переменных и его применение в приближенных вычислениях.
- •Решение типового варианта (задания 1-9).
- •1)Hайти пределы функций, пользуясь правилом Лопиталя (для случаев, когда оно применимо).
- •3)Найти первую производную неявной функции и функции, заданной параметрически.
- •5).Сделать разложение функции по формуле Тейлора при указанном значении :
- •6. Составить уравнение касательной и нормали к кривой в точке .
- •8. Дана функция . Показать, что .
- •9. Дана функция и точка . С помощью дифференциала вычислить приближенное значение функции в данной точке..
Задание 1. Hайти пределы функций (используя правило Лопиталя и др.)
1. 1)
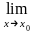
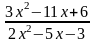 ;
при x0=
;
при x0=
2)
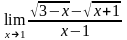 ;
;
3)
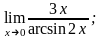
2. 1)

2)

3)
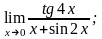
3. 1)
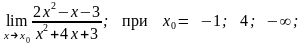
2)
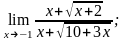
3)
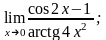
4. 1)
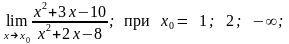
2)
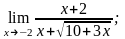
3)
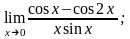
5. 1)
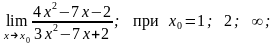
2)
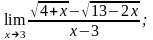
3)
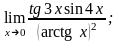
6. 1)

2)
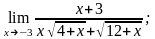
3)
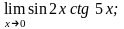
7. 1)
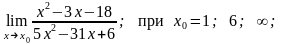
2)
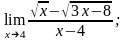
3)
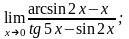
8. 1)
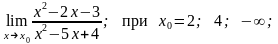
2)
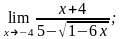
3)
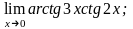
9. 1)

2)
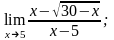
3)
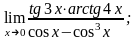
10. 1)

2)
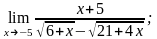
3)
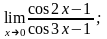
11. 1) ; при x0=
2) ;
3)
12. 1)
2)
3)
13. 1)
2)
3)
14. 1)
2)
3)
15. 1)
2)
3)
16. 1)
2)
3)
17. 1)
2)
3)
18. 1)
2)
3)
19. 1)
2)
3)
20. 1)
2)
3)
21. 1) ; при x0=
2) ;
3)
22. 1)
2)
3)
23. 1)
2)
3)
24. 1)
2)
3)
25. 1)
2)
3)
Задание 2. Найти производные функций, заданных в явном виде.
1. а)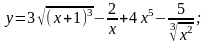
б)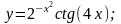
в)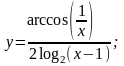
г)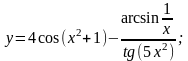
д)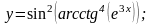
e)

2. a)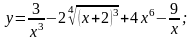
б)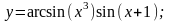
в)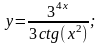
г)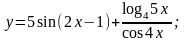
д)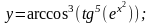
е)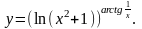
3.
а)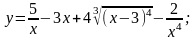
б)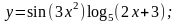
в)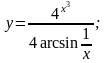
г)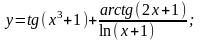
д)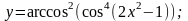
е)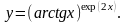
4.
а)
б)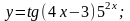
в)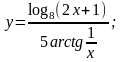
г)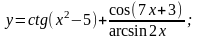
д)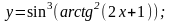
е)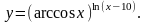
5. а)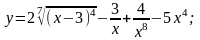
б)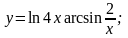
в)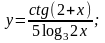
г)
д)
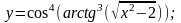
е)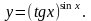
6. а)
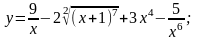
б)
в)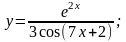
г)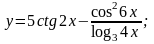
д)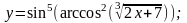
е)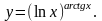
7.
а)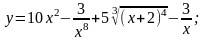
б)
в)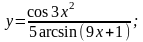
г)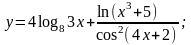
д)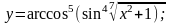
е)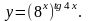
8
. а)
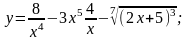
б)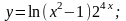

в)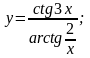
г)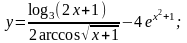
д)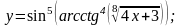
е)

9.
а)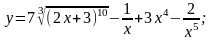
б)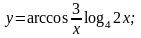
в)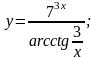
г)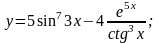
д)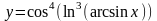
е)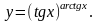
10.
а)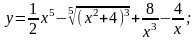
б)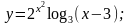
в)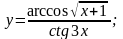
г)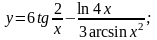
д)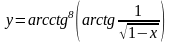 ;
;
е)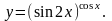
11. а)
б)
в)
г)
д)
e)
12. a)
б)
в)
г)
д)
е)
13. а)
б)
в)
г)
д)
е)
14. а)
б)
в)
г)
д)
е)
15. а)
б)
в)
г)
д)
е)
16. а)
б)
в)
г)
д)
е)
17. а)
б)
в)
г)
д)
е)
18 . а)
б)
в)
г)
д)
е)
19. а)
б)
в)
г)
д)
е)
20. а)
б)
в)
г)
д) ;
е)
21. а)
б)
в)
г)
д)
e)
22. a)
б)
в)
г)
д)
е)
23. а)
б)
в)
г)
д)
е)
24. а)
б)
в)
г)
д)
е)
25. а)
б)
в)
г)
д)
е)
Задание 3. Найти первую производную неявной функции и функции, заданной параметрически.
1.
а)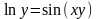 ;
;
б)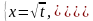
2.
а)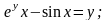
б)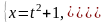
3.
а)
б)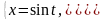
4.
а)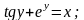
б)

5.
а)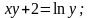
б)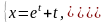
6. а)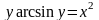 ;
;
б)
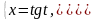
7.
а)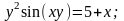
б)
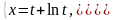
8.
а)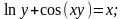
б)
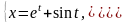
9.
а)
б)
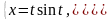
10. а)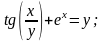
б)

11. а) ;
б)
12. а)
б)
13. а)
б)
14. а)
б)
15. а)
б)
16. а) ;
б)
17. а)
б)
18. а)
б)
19. а)
б)
20. а)
б)
21. а) ;
б)
22. а)
б)
23. а)
б)
24. а) ;
б)
25. а)
б)
Задание 4. Найти наименьшее и наибольшее значение функции на отрезке.
1.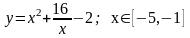 .
.
2.
 .
.
3.
 .
.
4.
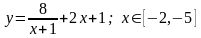 .
.
5.
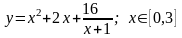 .
.
6.
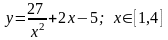 .
.
7.
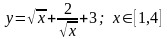 .
.
8.
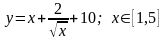 .
.
9.
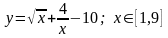 .
.
10.
 .
.
11. .
12. .
13. .
14. .
15. .
16. .
17. .
18. .
19. .
20. .
21. .
22. .
23. .
24. .
25. .
Задание
5.
Составить уравнение касательной и
нормали к кривой
 в точке А.
в точке А.
1.
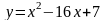 ;
A(0,7), 2.
;
A(0,7), 2.
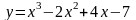 ;
A(1;-4);
;
A(1;-4);
3.
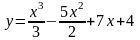 ;
A(0;4), 4.
;
A(0;4), 4.
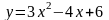 ;
A(1;5);
;
A(1;5);
5.
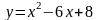 ;
A(1;3), 6.
;
A(1;3), 6.
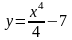 ;
A(2;-3);
;
A(2;-3);
7.
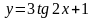 ;
A(/8;4); 8.
;
A(/8;4); 8.
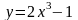 ;
A(1;1);
;
A(1;1);
9.
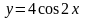 ;
A(0;4); 10.
;
A(0;4); 10.
 ;
A(2;10).
;
A(2;10).
11. ; A(0,7), 12. ; A(1;-4);
13. ; A(0;4), 14. ; A(1;5);
15. ; A(1;3), 16. ; A(2;-3);
17. ; A(/8;4); 18. ; A(1;1);
19. ; A(0;4); 20. ; A(2;10).
21. ; A(0,7), 22. ; A(1;-4);
23. ; A(0;4), 24. ; A(1;5);
25. ; A(1;3),
Задание 6. Провести полное исследование функции и построить ее график.
1.
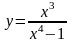 ; 2.
; 2.
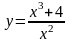 ;
;
3.
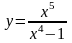 ; 4.
; 4.
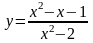 ;
;
5.
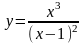 ; 6.
; 6.
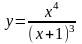 ;
;
7.
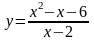 ; 8.
; 8.
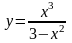 ;
;
9.
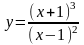 ; 10.
; 10.
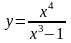 .
.
11. ; 12. ;
13. ; 14. ;
15. ; 16. ;
17. ; 18. ;
19. ; 20. .
21. ; 22. ;
23. ; 24. ;
25. .
Основные теоретические сведения для выполнения
Для
определённой в некоторой окрестности
точки
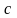 функции
функции
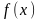 число
число
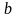 называется пределом функции
,
если при
называется пределом функции
,
если при
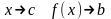 .
При этом пишут:
.
При этом пишут:
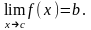
Если
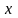 при стремлении к
принимает только значения, меньшие
,то
пишут:
при стремлении к
принимает только значения, меньшие
,то
пишут:
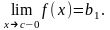
и
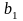 называют пределом функции
в точке с слева.
называют пределом функции
в точке с слева.
Если при стремлении к принимает только значения, большие ,то пишут:
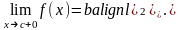
и
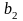 называют пределом функции
в точке с справа.
называют пределом функции
в точке с справа.
Функция
непрерывна в точке
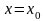 ,если
выполняется равенство:
,если
выполняется равенство:
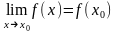 (1)
(1)
При
нахождении предела
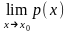 некоторой функции p(x) (x0- конечное
число или
некоторой функции p(x) (x0- конечное
число или
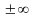 )
возможно появление неопределённостей
типа:
)
возможно появление неопределённостей
типа:
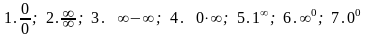 .
.
Неопределенности
типа
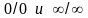 могут быть раскрыты по правилу Лопиталя:
могут быть раскрыты по правилу Лопиталя:
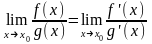 , (2)
, (2)
которое можно применять, пока существует неопределенность первого или второго типа. ( Понятие производной будет дано ниже).
Неопределённости типа 3-7 тождественными преобразованиями могут быть сведены к неопределенностям 1-ого или 2-ого типа.
Пример
1. Найти предел
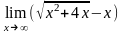 .
.
Имеем неопределённость 3-го типа. Умножив и разделив выражение на сопряжённое, получим неопределенность 2-го типа, которую легко раскрыть:
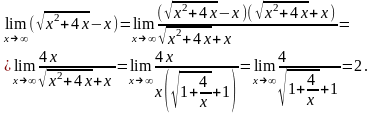
При нахождении пределов часто используются первый и второй замечательные пределы :
1)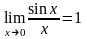 ;
2)
;
2)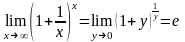 . (3)
. (3)
Пример
2. Найти предел
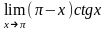 .
.
Имеем неопределённость 4-го типа. Применяя правило Лопиталя, найдём предел:
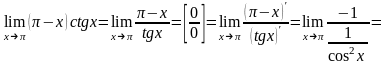
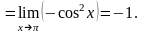
Пример
3. Найти предел:
 .
.
Имеем неопределенность 7-го типа. Обозначим искомый предел через А и прологарифмируем обе части равенства. Получим:
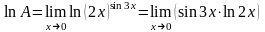 .
.
В правой части равенства имеем неопределенность 4-го типа. Преобразуем ее в неопределенность 1-го типа и раскроем по правилу Лопиталя:
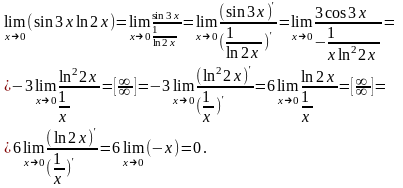
Т.о.
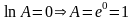 ,
т.е. искомый предел равен 1.
,
т.е. искомый предел равен 1.
Аналогично могут быть раскрыты неопределенности 5-го и 6-го типов.
Производной
функции
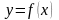 называется предел отношения приращения
функции
называется предел отношения приращения
функции
 к приращению аргумента
к приращению аргумента
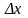 ,
когда
стремится к 0:
,
когда
стремится к 0:
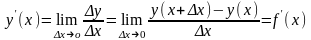 . (4)
. (4)
Кроме
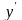 для производной функции
для производной функции
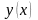 используются также обозначения
используются также обозначения
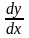 ,
где
,
где
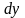 и
и
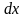 называются соответственно дифференциалом
функции
и дифференциалом аргумента
.
Дифференциалом первого порядка функции
называется та часть приращения функции
при приращении аргумента
,
которая линейно зависит от
.
Т.о., по определению дифференциал функции
равен произведению её производной на
дифференциал аргумента
:
называются соответственно дифференциалом
функции
и дифференциалом аргумента
.
Дифференциалом первого порядка функции
называется та часть приращения функции
при приращении аргумента
,
которая линейно зависит от
.
Т.о., по определению дифференциал функции
равен произведению её производной на
дифференциал аргумента
:
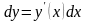 .
.
Геометрически
производная функции в точке x
представляет собой тангенс угла наклона
касательной к положительному направлению
оси Ox: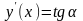 .
Т.к. производная характеризует скорость
изменения функции при изменении
аргумента, то физический смысл производной
по времени от вектора перемещения –
скорость
.
Т.к. производная характеризует скорость
изменения функции при изменении
аргумента, то физический смысл производной
по времени от вектора перемещения –
скорость
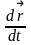 .
Производная по времени от скорости –
ускорение
.
Производная по времени от скорости –
ускорение
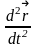 .
.
Операция нахождения производной функции называется дифференцированием функции.
Если
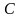 – константа, а
– константа, а
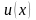 и
и
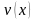 – дифференцируемые функции, то справедливы
следующие правила дифференцирования:
– дифференцируемые функции, то справедливы
следующие правила дифференцирования:

6.
Если
сложная функция от
,
т.е. у = ур(х),
где у(р) и р(х) – дифференцируемые функции,
то
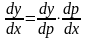 или
или
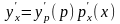 . (5)
. (5)
Используя формулу (4) для производной функции и правила дифференцирования, можно получить таблицу производных основных элементарных функций:
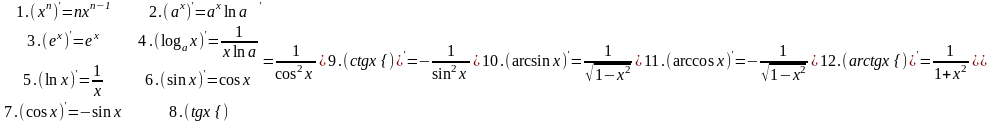
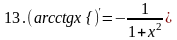
Производную
сложной показательной функции
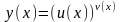 легко найти, предварительно прологарифмировав
обе части равенства. В результате
получим:
легко найти, предварительно прологарифмировав
обе части равенства. В результате
получим:
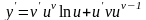 . (6)
. (6)
Производная
от первой производной функции
обозначается
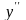 или
или
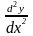 и называется производной 2-го порядка
или второй производной.
и называется производной 2-го порядка
или второй производной.
Производной
n-го порядка функции
,
если она существует, называется
производная от производной (n-1)-го порядка
и обозначается
 или
или
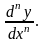
Если
функция
задана неявно и определяется уравнением
 ,
то дифференцируя обе части равенства
по
получим уравнение первой степени
относительно
,
из которого найдём
,
как некоторую функцию от
и
,
то дифференцируя обе части равенства
по
получим уравнение первой степени
относительно
,
из которого найдём
,
как некоторую функцию от
и
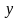 :
:
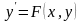 .
.
Дифференцируя по обе части последнего равенства и используя выражение для , можно получить выражение для второй производной .
Пример 4.
Найти
и
,
если
задано неявно уравнением
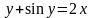 .
.
Приведём уравнение к виду .
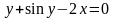 ;
;
продифференцировав, получим :
(а) 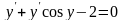 .
.
Откуда
(б) 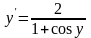 .
.
Продифференцируем по обе части равенства (а):
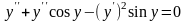
(в) 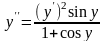 .
.
Подставляя в (в) из (б) получим:
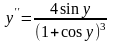 .
.
Если
функция
задана в параметрическом виде
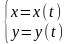 ,
то производные определяются формулами:
,
то производные определяются формулами:
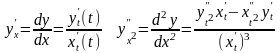 (7)
(7)
Пример 5.
Найти
 ,
если
,
если
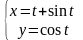
Используя формулу (7) получим :
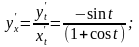
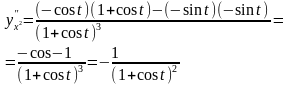
Если
существуют производные любого порядка
функции
,
то функция
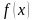 может быть записана в виде
может быть записана в виде
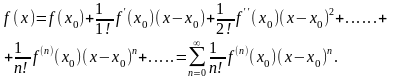 (8)
(8)
где
под знаком суммы производная нулевого
порядка
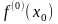 принимается равной
принимается равной
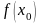 ;
n!=
;
n!=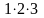 ...n;
0!=1. Формула (8) называется формулой
Тейлора разложения функции
в точке
...n;
0!=1. Формула (8) называется формулой
Тейлора разложения функции
в точке
 по степеням
по степеням
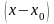 .
При этом предполагается, что правая
часть формулы (8) должна быть ограниченной
функцией от
.
.
При этом предполагается, что правая
часть формулы (8) должна быть ограниченной
функцией от
.
При
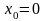 из (8) получим:
из (8) получим:
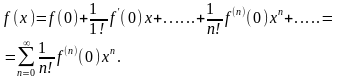 (9)
(9)
Формула
(9) называется формулой Маклорена
разложения функции
в точке
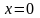 по степеням
.
по степеням
.
Пример 6.
Разложить
функцию
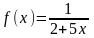 по формуле Тейлора в точке
по формуле Тейлора в точке
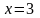 .
.
Вычисляем
производные функции
и увидев закономерность, запишем
выражение для производной n-го порядка
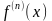 :
:
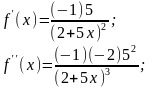
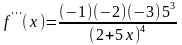 .
.
Легко увидеть, что имеет следующий вид:
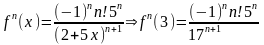 .
.
Подставляя
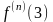 в
формулу (9), получим :
в
формулу (9), получим :
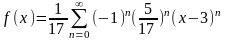 .
.
