Функции нескольких переменных и их дифференцирование.

Определение: Переменная z называется функцией переменных x è y, если каждой паре значений x и y поставлено в соответствие определенное значение z.

Функциональная зависимость z от x и y записывается в виде z=f(x,y). Аналогичным образом определяются функции трех и более переменных.

Функции двух переменных допускают геометрическую интерпретацию. Графиком функции z=f(x,y), определенной в области G, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежат G и z=f(x,y). В наиболее простых случаях такой график представляет собой поверхность (рис. 3).

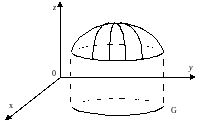
Рис. 3

Частной производной функции нескольких переменных по какой-либо переменной в рассматриваемой точке называется обычная производная по этой переменной. При этом другие переменные считаются фиксированными (постоянными).

Для функции z=f(x,y) в точке A(x₀;y₀) частные производные определяются следующим образом:

если эти пределы существуют.

Из определения частных производных следует, что правила их вычисления остаются такими же, как и для функции одной переменной, только необходимо помнить, по какой переменной ищется производная.

Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка.

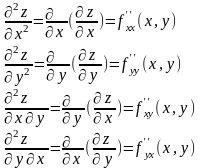
Частные переменные и называются смешанными. В теории доказывается, что в тех точках, где производные непрерывны, смешанные производные совпадают.

Найдем частные производные второго порядка функции 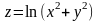. Сначала вычислим частные производные первого порядка

.

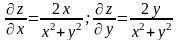Тогда

Видно, что смешанные производные равны

.

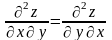Пример 3. Дана функция .

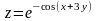Показать, что ; где .

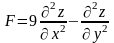Решение: вычислим сначала а затем и .

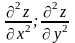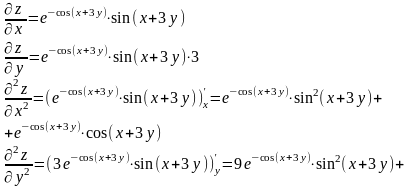
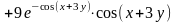
Тогда

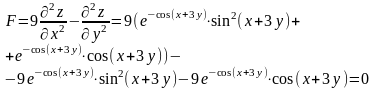
Ответ: , что и требовалось доказать.

Полный дифференциал функции двух переменных и его применение в приближенных вычислениях.

Пусть задана функция двух переменных 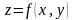. Легко доказать, что если приращение функции

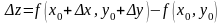(4)

можно представить в виде

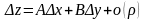, (5)

где и - некоторые константы, а 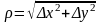, то в точке 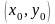существуют частные производные этой функции, причем

, .

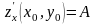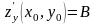Таким образом, при условии существования частных производных функции 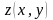в точке выражение (5) можно записать в виде:

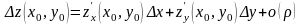. (6)

При выполнении формулы (6) функция называется дифференцируемой в точке и выражение

,

то есть линейная часть приращения функции называется ее полным дифференциалом и обозначается символом 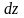или .

Под дифференциалами независимых переменных понимают произвольные приращения , , поэтому полный дифференциал функции можно записать в виде:

или

.

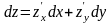Слагаемые, стоящие в правой части последнего равенства называются частными дифференциалами функции . Таким образом, полный дифференциал функции равен сумме ее частных дифференциалов.

Полный дифференциал функции нескольких переменных (в нашем случае двух) с успехом применяется в приближенных вычислениях при оценке погрешностей. Пусть, например, мы имеем функцию двух переменных. При определении значений независимых переменных и будем допускать погрешности и соответственно. Тогда значение , вычисленное по неточным значениям аргументов, также получится с погрешностью

.

Оценим эту погрешность.

Заменим приближенно приращение функции ее дифференциалом (это оправдано лишь при достаточно малых значениях и ). Получим

.

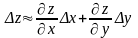Здесь и погрешности , , и коэффициенты при них могут быть как положительными, так и отрицательными; заменяя те и другие их абсолютными величинами, придем к неравенству:

.

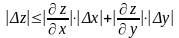Если через 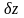, , 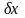обозначить максимальные абсолютные погрешности (или границы для абсолютных погрешностей), то можно, очевидно, принять

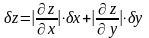. (7)

При этом само приближенное значение функции вычисляется по формуле:

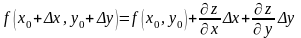. (8)

Пример 4. Дана функция 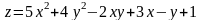и точка 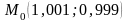. С помощью дифференциала вычислить приближенные значения функции в данной точке.

Пусть 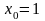, , тогда , .

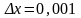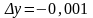По формуле (8) вычислим значение функции:

.

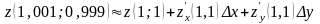Вычислим отдельно частные производные заданной функции:

;

.

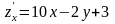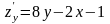Вычислим значения функции и частных производных в точке :

;

;

.

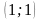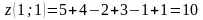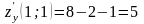Тогда

Ответ: