
- •Основные теоретические сведения для выполнения
- •Приложения производной к задачам геометрии.
- •Полное исследование функций и построение графика.
- •Функции нескольких переменных и их дифференцирование.
- •Полный дифференциал функции двух переменных и его применение в приближенных вычислениях.
- •Решение типового варианта (задания 1-9).
- •1)Hайти пределы функций, пользуясь правилом Лопиталя (для случаев, когда оно применимо).
- •3)Найти первую производную неявной функции и функции, заданной параметрически.
- •5).Сделать разложение функции по формуле Тейлора при указанном значении :
- •6. Составить уравнение касательной и нормали к кривой в точке .
- •8. Дана функция . Показать, что .
- •9. Дана функция и точка . С помощью дифференциала вычислить приближенное значение функции в данной точке..
Приложения производной к задачам геометрии.
Если
кривая задана уравнением
,
то угол
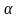 ,
образованный касательной к кривой в
точке
с положительным направлением оси
,
образованный касательной к кривой в
точке
с положительным направлением оси
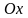 ,
находится из уравнения
,
находится из уравнения
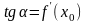 . (1)
. (1)
Уравнение
касательной к кривой
в точке
 имеет вид
имеет вид
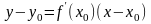 , (2)
, (2)
где
 есть значение производной
при
.
Нормалью к кривой называется прямая,
перпендикулярная касательной и проходящая
через точку касания. Уравнение нормали
имеет вид
есть значение производной
при
.
Нормалью к кривой называется прямая,
перпендикулярная касательной и проходящая
через точку касания. Уравнение нормали
имеет вид
 . (3)
. (3)
Пример
1: Составить уравнения касательной и
нормали к кривой
 ,
проведенной в точке
,
проведенной в точке
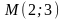 .
Найти угол, образованный касательной
с осью абсцисс.
.
Найти угол, образованный касательной
с осью абсцисс.
Решение: Найдем сначала
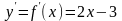 ,
,
подставляя
координату
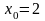 точки
точки
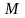 получаем
получаем
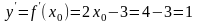 .
.
Из
(1) получаем:
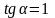 ;
тогда
;
тогда
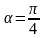 .
Подставляя
.
Подставляя
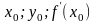 в формулу (2) находим уравнение касательной
в формулу (2) находим уравнение касательной
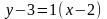 или
или
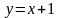 .
.
Аналогично из формулы (3) выводим уравнение нормали
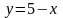 .
.
Ответ:
уравнение касательной
;
нормали
;угол
с осью абсцисс
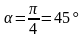 .
.
Полное исследование функций и построение графика.
Для полного исследования функции и построения ее графика рекомендуется следующая схема:
А) найти область определения, точки разрыва; исследовать поведение функции вблизи точек разрыва (найти пределы функции слева и справа в этих точках). Указать вертикальные асимптоты.
Б)
определить четность или нечетность
функции и сделать вывод о наличии
симметрии. Если
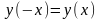 ,
то функция четная, симметрична относительно
оси OY; при
,
то функция четная, симметрична относительно
оси OY; при
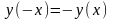 функция нечетная, симметрична относительно
начала координат; а если
функция нечетная, симметрична относительно
начала координат; а если
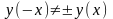 –
функция общего вида.
–
функция общего вида.
В)
найти точки пересечения функции с осями
координат OY и OX
(если это возможно), определить интервалы
знакопостоянства функции. Границы
интервалов знакопостоянства функции
определяются точками, в которых функция
равна нулю(нули функции) или не существует
и границами области определения этой
функции. В интервалах, где
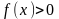 график функции расположен над осью OX,
а где
график функции расположен над осью OX,
а где
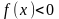 –
под этой осью.
–
под этой осью.
Г)
найти первую производную
функции, определить ее нули и интервалы
знакопостоянства. В интервалах, где
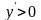 функция возрастает, а где
функция возрастает, а где
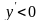 убывает. Сделать заключение о наличие
экстремумов (точек, где функция и
производная существуют и при переходе
через которые
меняет знак. Если
меняет знак с плюса на минус, то в этой
точке функция имеет максимум, а если с
минуса на плюс, то минимум). Найти значения
функции в точках экстремумов.
убывает. Сделать заключение о наличие
экстремумов (точек, где функция и
производная существуют и при переходе
через которые
меняет знак. Если
меняет знак с плюса на минус, то в этой
точке функция имеет максимум, а если с
минуса на плюс, то минимум). Найти значения
функции в точках экстремумов.
Д)
найти вторую производную
,
ее нули и интервалы знакопостоянства.
В интервалах, где
<
0 график функции выпуклый, а где
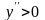 – вогнутый. Сделать заключение о наличии
точек перегиба и найти значения функции
в этих точках.
– вогнутый. Сделать заключение о наличии
точек перегиба и найти значения функции
в этих точках.
Е)
найти наклонные (горизонтальные)
асимптоты, уравнения которых имеют вид
 ;
где
;
где
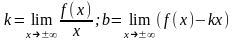 .
.
При
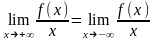 график
функции будет иметь две наклонные
асимптоты, причем каждому значению x
при
график
функции будет иметь две наклонные
асимптоты, причем каждому значению x
при
 и
и
 могут соответствовать и два значения
b.
могут соответствовать и два значения
b.
Ж) найти дополнительные точки для уточнения графика (если в этом есть необходимость) и построить график.
Пример
2. Исследовать функцию
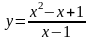 и построить ее график.
и построить ее график.
Решение:
А) область определения
 ;
функция непрерывна в области определения;
;
функция непрерывна в области определения;
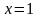 – точка разрыва, т.к.
– точка разрыва, т.к.
 ;
;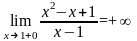 . Тогда
–
вертикальная асимптота.
. Тогда
–
вертикальная асимптота.
Б)
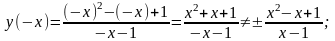
т.е. y(x)– функция общего вида.
В) Находим точки пересечения графика с осью OY: полагаем x=0; тогда y(0)=–1, т.е. график функции пересекает ось в точке (0;-1). Нули функции (точки пересечения графика с осью OX): полагаем y=0; тогда
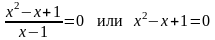 .
.
Дискриминант квадратного уравнения меньше нуля, значит нулей не существует. Тогда границей интервалов знакопостоянства является точка x=1, где функция не существует.
Знак функции в каждом из интервалов определяем методом частных значений:
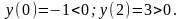
Из
схемы видно, что в интервале
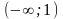 график
функции расположен под осью OX,
а в интервале
график
функции расположен под осью OX,
а в интервале
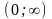 –над
осью OX.
–над
осью OX.
Г) Выясняем наличие критических точек.
 .
.
Критические
точки (где
 или не существует) находим из равенств
или не существует) находим из равенств
 и
и
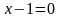 .
Получаем: x1=1,
x2=0,
x3=2.
Составим вспомогательную таблицу
.
Получаем: x1=1,
x2=0,
x3=2.
Составим вспомогательную таблицу
Таблица 1

(В первой строке записываются критические точки и интервалы, на которые делят эти точки ось OX; во второй строке указываются значения производной в критических точках и знаки на интервалах. Знаки определяются методом частных значений. В третьей строке указываются значения функции y(x) в критических точках и показывается поведение функции – возрастание или убывание на соответствующих интервалах числовой оси. Дополнительно обозначается наличие минимума или максимума.
Д) Находим интервалы выпуклости и вогнутости фукнции.
 ;
строим таблицу как в пункте Г); только
во второй строке записываем знаки
,
а в третьей указываем вид выпуклости.
Т.к.
;
строим таблицу как в пункте Г); только
во второй строке записываем знаки
,
а в третьей указываем вид выпуклости.
Т.к.
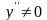 ;
то критическая точка одна x=1.
;
то критическая точка одна x=1.
Таблица 2

Точка x=1 является точкой перегиба; т.к.
Е) Находим наклонные и горизонтальные асимптоты
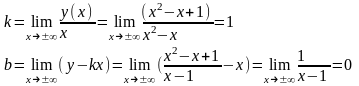
Тогда y=x – наклонная асимптота.
Ж) По полученным данным строим график функции
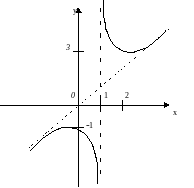
Рис. 2
