- •Классификация параллельных кс по структурно-функциональным признакам.
- •Классификация параллельных кс по функциональным возможностям кс с точки зрения пользователя
- •Проведите сравнительный анализ классификаций компьютерных систем.
- •Мультикомпьютеры, кластеры и симметричные мультипроцессоры общая характеристика, схемы построения, особенности каждой из систем, области применения.
- •Системы с распределенной и разделяемой памятью, массово-параллельные системы общая характеристика, схема построения, особенности каждой из систем, области применения.
- •Преимущества архитектуры
- •Недостатки архитектуры
- •Основные понятия теории моделирования параллельных кс. Методы моделирования параллельных кс.
- •Задачи моделирования параллельных кс.
- •Приведите основные принципы моделирования.
- •Моделирование параллельных процессов. Применение аппарата сетей Петри.
- •Подклассы сетей Петри:
- •Применение сетей Петри для синтеза дискретных управляющих устройств.
- •Оценочные или е-сети как расширение сетей Петри
- •Моделирование конвейерной обработки информации
- •Свойства сохранения и активности сети Петри
- •Свойство достижимости и покрываемости сети Петри.
- •Свойство безопасности и ограниченности сети Петри.
- •Анализ сетей Петри матричным методом
- •Матричный метод анализа сетей Петри достоинства и недостатки метода
- •Задачи достижимости и покрываемости сети Петри.
- •Границы возможности моделирования с помощью сетей Петри
- •Подклассы сетей Петри:
- •Маркированные графы подкласс сетей Петри
- •Сети Петри и их особенности
- •Разбиения чисел. Основные понятия и определения. Принцип Дирихле.
- •Вложимость разбиений.
- •Ранговое условие вложимости; пример использования.
- •Принцип полного размещения; пример использования.
- •Вложимость с ограничениями; пример использования.
- •Особенностью распределения памяти в кс с сегментной организацией программ и данных (модель 2). Приведите пример.
- •Комбинаторная модель для оценки необходимого размера памяти кс (модель 4). Приведите пример.
- •Комбинаторная модель, позволяющая произвести расчет оценки сверху необходимого размера оперативной памяти кс.
- •Диаграммы Ферре и инверсия в бинарных последовательностях
- •Надежность кольцевой структуры кс (для сети [n,2]).
- •Надежность сети кс.
- •Связанные случайные величины
- •Детерминированные меры живучести для многополюсных сетей
- •Матричная теорема о деревьях для графов (пример)
- •Теорема Кирхгофа-Трента
- •Каркасы в ориентированных графах
- •Надежность сети относительно одного источника и многих стоков
Оценочные или е-сети как расширение сетей Петри
Е-сети (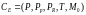
P – множество позиций,
Pp множество периеритных позиций
PR множество решающих позиций
T – множество переходов причем ti = ( ρS, t(ti) )
S – тип перехода ( 1- 5 ), t(ti) время перехода, ρ(ti) – функция перехода, функция преобразования атрибута меток.
В Е-сетях метки интерпретируются, как транзакты, распространяющиеся по сети, а вершины и переходы трактуются как устройства обработки транзактов. Требование – ни одна вершина не может иметь более 1 метки (т.е. сеть изначально безопасна).
Типы переходов:
1. простой переход, срабатывает при наличии фишки в P1 и отсутствии в P2, моделирование некоторого устройства обработки инф.
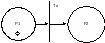
2. разветвление потока транзактов в ВС.
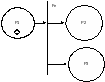
3. объединение наличие фишек P2, P3 и отсутствие в P1
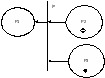
4. управляющие разветвление изменяет направление потока транзактов.
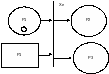
5. приоритетность одних потоков к другим
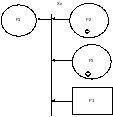
Моделирование конвейерной обработки информации
На протяжении последних лет было предпринято множество шагов направленных на увеличение производительности ВС. Результатом одного из таких шагов было появление ВС с конвейерной обработкой информации. Конвейер состоит из набора операций, которые могут выполняться параллельно. Когда операция k завершена, она передает свой результат (k+1)-й операции и ждет данных от (k-1)-й.
В качестве примера рассмотрим сложение 2 чисел с плавающей точкой. Основные шаги этой операции предполагают:
Выделить экспоненты этих 2 чисел
Сравнить эти экспоненты, и если необходимо изменить их должным образом
Сдвинуть точку в числе с меньшей экспонентой для их уравнения
Сложить дроби
Нормализовать результат
Проверить экспоненту на переполнение и сформировать экспоненту и дробь результата
Конвейеры (по способу управления) можно разделить на 2 группы: синхронные и асинхронные. Синхронные конвейеры каждый такт передают данные на следующий шаг обработки. Но это не эффективно, т.к. действие, выполняемое на данном шаге, может занимать времени больше/меньше чем 1 такт. Рассмотрим k-й блок конвейера. Для управления им нужно знать, когда выполняются следующие условия:
В
 ходной
регистр заполнен
ходной
регистр заполненВходной регистр пуст
Выходной регистр заполнен
Выходной регистр пуст
Блок занят
Блок свободен
Пересылка осуществлена

Свойства сохранения и активности сети Петри
Сохранение
Сети Петри можно использовать для моделировании систем распределения ресурсов. Например, сеть Петри может моделировать запросы, распределения и освобождения устройств ввода-вывода в вычислительной системе. В этих системах некоторые фишки могут представлять ресурсы. Группа из трех построчно печатающих устройств представляется позицией, имеющей в начальной маркировке три фишки. Запрос построчно-печатающего устройства – это переход, для которого данная позиция является входной; затем устройство освобождается переходом, для которого позиция построчно печатающих устройств является выходной.
Для сетей Петри такого типа помимо прочих важным свойством является сохранение. Нам бы хотелось показать, что фишки, представляющие ресурсы, никогда не создаются и не уничтожаются. Простейший способ это сделать – это потребовать, чтобы общее число фишек в сети оставалось постоянным.
Def. Сеть Петри
C=(P,T,I,O)
с начальной маркировкой
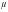 называется строго сохраняющей,
если для всех
называется строго сохраняющей,
если для всех
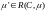 имеет место
имеет место
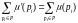 .
.
Строгое сохранение – это очень сильное
ограничение. Например, из него немедленно
следует, что число входов в каждый
переход должно равняться числу выходов
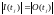 .
Если бы это было не так, запуск перехода
изменил бы число фишек в сети.
.
Если бы это было не так, запуск перехода
изменил бы число фишек в сети.
Фишка определяется ее позицией в сети,
все фишки в позиции неразличимы. Фишка
может представлять разное количество
ресурсов. В общем случае необходимо
определить веса фишек. Т.к. фишки в
позиции не различимы, веса связываются
с каждой позицией сети. Вектор взвешивания
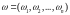 определяет вес
определяет вес
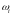 для каждой позиции
для каждой позиции
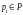 .
.
Def. Сеть Петри
C=(P,T,I,O)
с начальной маркировкой
называется сохраняющей по
отношению к вектору взвешивания
,
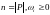 если для всех
имеет место
если для всех
имеет место
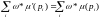
Строго сохраняющая сеть Петри является сохраняющей по отношению в вектору взвешивания (1, 1, … ,1).
Все сети Петри являются сохраняющими
по отношения к вектору взвешивания
(0,0,…, 0). Поэтому сеть Петри называют
сохраняющей, если она сохраняющая по
отношению к каком-нибудь положительному
не нулевому вектору
 .
.
Активность
Причиной рассмотрения сохранения в сети Петри было распределение ресурсов в операционной системе ЭВМ. Другая задача. Которая может возникнуть при распределении ресурсов вычислительной системы – тупики.
Рассмотрим простой пример.

Система включает 2 различных ресурса q и r и два процесса a и b. Если оба процесса нуждаются в обоих ресурсах, им необходимо будет совместно использовать ресурсы. Для выполнения этого потребуем, чтобы каждый процесс запрашивал ресурс, а затем освобождал его. Теперь предположим, что процесс a сначала запрашивает ресурс q, а затем ресурс r и наконец, освобождает и q и r. Процесс b работает аналогично, но сначала запрашивает ресурс r, а потом q.
Начальная маркировка помечает ресурсы
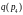 и
и
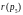 доступными
и указывает на готовность процессов a
и b. Одним выполнением этой сети является
доступными
и указывает на готовность процессов a
и b. Одним выполнением этой сети является
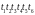 ;
другим -
;
другим -
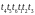 .
Ни одно из этих выполнений не приводит
к тупику. Однако рассмотрим
последовательность, которая начинается
переходами
.
Ни одно из этих выполнений не приводит
к тупику. Однако рассмотрим
последовательность, которая начинается
переходами
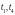 :
процесс a обладает ресурсом q и хочет
получить ресурс r, а процесс b обладает
ресурсом r и хочет получить ресурс q.
Система заблокирована; никакой процесс
продолжаться не может.
:
процесс a обладает ресурсом q и хочет
получить ресурс r, а процесс b обладает
ресурсом r и хочет получить ресурс q.
Система заблокирована; никакой процесс
продолжаться не может.
Тупик в сети Петри – переход (или
множество переходов), которые не могут
быть запущены. В сети Петри на рисунке
4,6 тупик возникает, если нельзя запустить
переходы
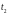 и
и
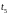 .
Переход называется активным, если он
не заблокирован (нетупиковый).
.
Переход называется активным, если он
не заблокирован (нетупиковый).
Переход
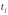 в сети Петри С называется потенциально
запустимым в маркировке
,
если существует маркировка
,
в которой
разрешен. Переход активен в маркировке
,
если потенциально запустим во всякой
маркировке из
в сети Петри С называется потенциально
запустимым в маркировке
,
если существует маркировка
,
в которой
разрешен. Переход активен в маркировке
,
если потенциально запустим во всякой
маркировке из
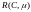 .
Следовательно, если переход активен,
то всегда возможно перевести сеть Петри
из ее текущей маркировки, в маркировку
в которой запуск перехода станет
разрешенным.
.
Следовательно, если переход активен,
то всегда возможно перевести сеть Петри
из ее текущей маркировки, в маркировку
в которой запуск перехода станет
разрешенным.
Другие понятия, связанные с изучением тупиков, можно разбить на категории по уровню активности и определить для сетей Петри С с маркировкой следующим образом:
Уровень 0: Переход обладает активностью уровня 0, если он никогда не может быть запущен.
Уровень 1: Переход
обладает активностью уровня 1, если
он потенциально запустим, т.е. если
существует такая
,
что
разрешен в
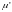 .
.
Уровень 2: Переход обладает активностью уровня 2, если для всякого целого n существует последовательность запусков, в которой присутствует неограниченно часто.
Уровень 3: Переход обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой присутствует неограниченное число раз.
Уровень 4: Переход
обладает активностью уровня 4, если
для всякой
существует такая последовательность
запусков
 ,
что
разрешены в
,
что
разрешены в
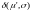
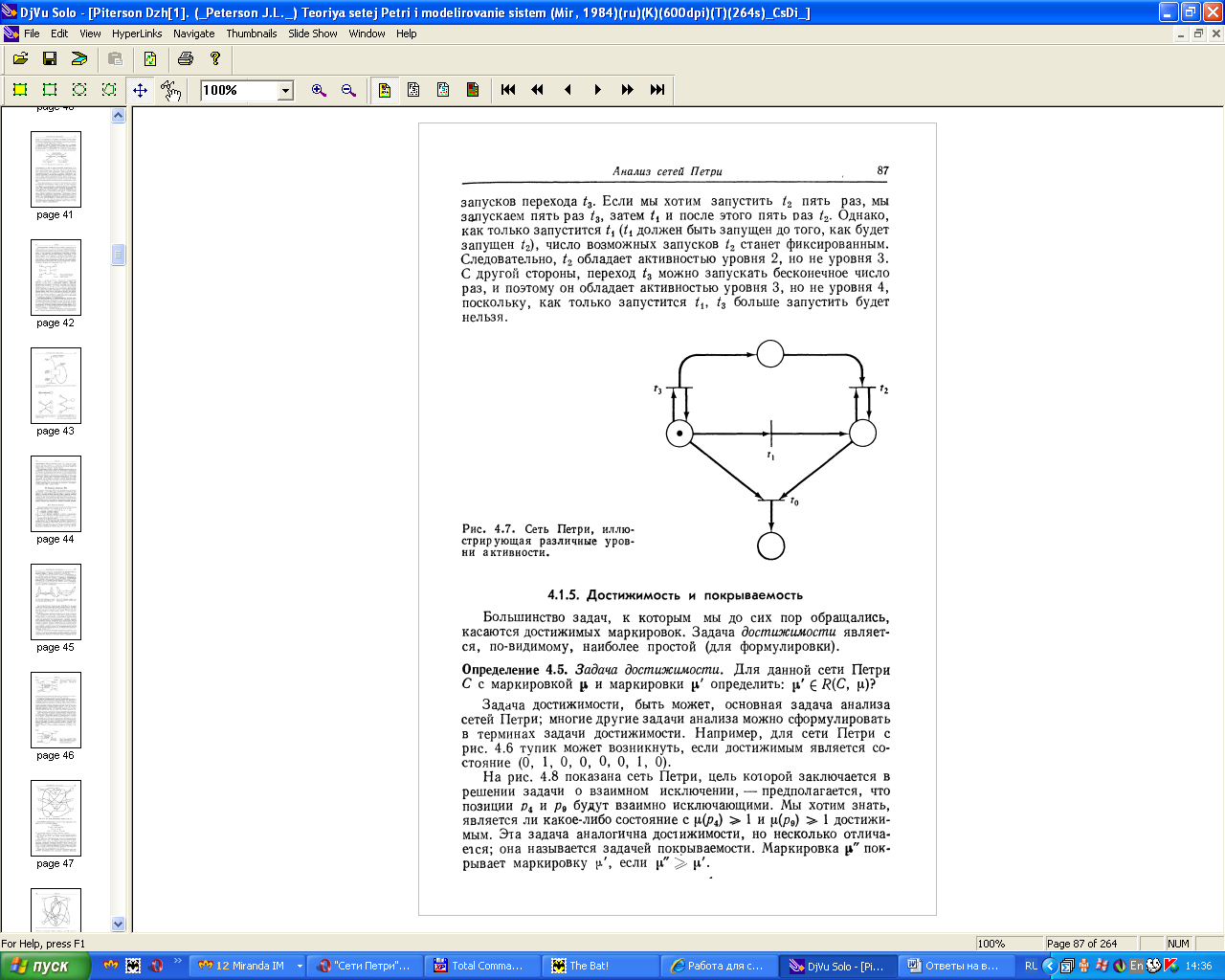
Переход, обладающий уровнем активности 0, называется пассивным; активностью 4, называется активным. Сеть Петри обладает активностью уровня i, если каждый ее переход обладает активностью уровня i.
Переход
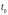 не может быть запущен никогда, он
пассивен. Переход
не может быть запущен никогда, он
пассивен. Переход
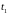 может быть запущен ровно 1 раз, он обладает
активностью уровня 1. Переход
может быть запущен произвольное число
раз, но это число зависит от числа
запусков перехода
может быть запущен ровно 1 раз, он обладает
активностью уровня 1. Переход
может быть запущен произвольное число
раз, но это число зависит от числа
запусков перехода
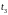 .
Если мы хоти запустить
5 раз, то мы запускаем 5 раз
,
затем
и после этого 5 раз
.
Однако, как только запустится
число запусков
станет фиксированным. Следовательно
обладает активностью уровня 2. Переход
может быть запущен неограниченное число
раз, и поэтому обладает активностью
уровня 3, но не уровня 4, поскольку, как
только запустится
,
больше запустить будет нельзя.
.
Если мы хоти запустить
5 раз, то мы запускаем 5 раз
,
затем
и после этого 5 раз
.
Однако, как только запустится
число запусков
станет фиксированным. Следовательно
обладает активностью уровня 2. Переход
может быть запущен неограниченное число
раз, и поэтому обладает активностью
уровня 3, но не уровня 4, поскольку, как
только запустится
,
больше запустить будет нельзя.