
- •Классификация параллельных кс по структурно-функциональным признакам.
- •Классификация параллельных кс по функциональным возможностям кс с точки зрения пользователя
- •Проведите сравнительный анализ классификаций компьютерных систем.
- •Мультикомпьютеры, кластеры и симметричные мультипроцессоры общая характеристика, схемы построения, особенности каждой из систем, области применения.
- •Системы с распределенной и разделяемой памятью, массово-параллельные системы общая характеристика, схема построения, особенности каждой из систем, области применения.
- •Преимущества архитектуры
- •Недостатки архитектуры
- •Основные понятия теории моделирования параллельных кс. Методы моделирования параллельных кс.
- •Задачи моделирования параллельных кс.
- •Приведите основные принципы моделирования.
- •Моделирование параллельных процессов. Применение аппарата сетей Петри.
- •Подклассы сетей Петри:
- •Применение сетей Петри для синтеза дискретных управляющих устройств.
- •Оценочные или е-сети как расширение сетей Петри
- •Моделирование конвейерной обработки информации
- •Свойства сохранения и активности сети Петри
- •Свойство достижимости и покрываемости сети Петри.
- •Свойство безопасности и ограниченности сети Петри.
- •Анализ сетей Петри матричным методом
- •Матричный метод анализа сетей Петри достоинства и недостатки метода
- •Задачи достижимости и покрываемости сети Петри.
- •Границы возможности моделирования с помощью сетей Петри
- •Подклассы сетей Петри:
- •Маркированные графы подкласс сетей Петри
- •Сети Петри и их особенности
- •Разбиения чисел. Основные понятия и определения. Принцип Дирихле.
- •Вложимость разбиений.
- •Ранговое условие вложимости; пример использования.
- •Принцип полного размещения; пример использования.
- •Вложимость с ограничениями; пример использования.
- •Особенностью распределения памяти в кс с сегментной организацией программ и данных (модель 2). Приведите пример.
- •Комбинаторная модель для оценки необходимого размера памяти кс (модель 4). Приведите пример.
- •Комбинаторная модель, позволяющая произвести расчет оценки сверху необходимого размера оперативной памяти кс.
- •Диаграммы Ферре и инверсия в бинарных последовательностях
- •Надежность кольцевой структуры кс (для сети [n,2]).
- •Надежность сети кс.
- •Связанные случайные величины
- •Детерминированные меры живучести для многополюсных сетей
- •Матричная теорема о деревьях для графов (пример)
- •Теорема Кирхгофа-Трента
- •Каркасы в ориентированных графах
- •Надежность сети относительно одного источника и многих стоков
Подклассы сетей Петри:
Простой
сетью Петри называется набор
![]() ,
где
,
где
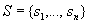 -
множество мест;
-
множество мест;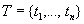 -
множество переходов таких, что
-
множество переходов таких, что
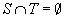 .
. -
отношение инцидентности такое,
что:
-
отношение инцидентности такое,
что:
Регулярные сети (вводится алгебра регулярных сетей, строятся операции над сетями и классы элементарных сетей).
Чистые сети (переход не может иметь позицию Pi в качестве входной и выходной).
Сети
свободного выбора (этот подкласс
допускает и конфликты автоматных сетей
Петри, и параллельность маркированных
графов, но в более ограниченном виде,
чем в обычных сетях Петри. Сеть Петри
со свободным выбором есть сеть Петри С
= (Р, Т, I, О) — такая, что
для всех
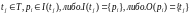 Важность этого определения заключается
в том способе, которым оно допускает
управляемые конфликты. Конфликт
появляется только тогда, когда одна
позиция является входом нескольких
переходов. По определению сетей Петри
со свободным выбором, если позиция
является входом для нескольких переходов
(потенциальный конфликт), то она является
единственным входом всех этих переходов.
Следовательно, либо все эти конфликтующие
переходы одновременно являются
разрешенными, либо ни один из них. Это
позволяет свободно осуществлять выбор
(разрешение конфликта) запускаемого
перехода, присутствие фишек в других
позициях не влияет на выбор запускаемого
перехода.
Важность этого определения заключается
в том способе, которым оно допускает
управляемые конфликты. Конфликт
появляется только тогда, когда одна
позиция является входом нескольких
переходов. По определению сетей Петри
со свободным выбором, если позиция
является входом для нескольких переходов
(потенциальный конфликт), то она является
единственным входом всех этих переходов.
Следовательно, либо все эти конфликтующие
переходы одновременно являются
разрешенными, либо ни один из них. Это
позволяет свободно осуществлять выбор
(разрешение конфликта) запускаемого
перехода, присутствие фишек в других
позициях не влияет на выбор запускаемого
перехода.
Сети, свободные от конфликтов, если Pi принадлежит I( tj), то Pi принадлежит О( tj), иначе Pi должна иметь <= 1 выходной переход.
Устойчивые сети (для такой сети маркировка принадлежит множеству допустимых маркировок, если 2 любых перехода оказываются в возбужденном состоянии, то срабатывает один из них не исключая возможности срабатывания другого )
Автоматные графы (каждый переход может иметь точно один выход и один вход)
Маркированный граф – сеть Петри
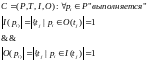
Расширение сетей Петри.
Е-сети
Сети Мерлина
Временные сети
Раскрашенные сети
Приоритетные сети
Сети с проверкой на ноль
Обобщенные сети.
Применение сетей Петри для синтеза дискретных управляющих устройств.
Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События - это действия, имеющие место в системе. Возникновением событий управляет состояние системы. Состояние системы может быть описано множеством условий. Условие — есть предикат или логическое описание состояния системы. Условие может принимать либо значение «истина», либо значение «ложь». Так как события являются действиями, то они могут происходить. Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение предусловий и может привести к выполнению других условий, постусловий.
В качестве примера рассмотрим задачу моделирования простого автомата-продавца. Автомат-продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются:
а) автомат-продавец ждет;
б) заказ прибыл и ждет;
в) автомат-продавец выполняет заказ;
г) заказ выполнен.
Событиями будут:
1. Заказ поступил.
2. Автомат-продавец начинает выполнение заказа.
3. Автомат-продавец заканчивает выполнение заказа.
4. Заказ посылается на доставку.
Предусловия события 2 (автомат-продавец начинает выполнение заказа) очевидны:
(а) автомат-продавец ждет; (б) заказ прибыл и ждет.
Постусловие для события 2:
(в) автомат-продавец выполняет заказ.
Аналогично мы можем определить предусловия и постусловия для других событий и составить следующую таблицу событий и их пред- и постусловий:
Событие |
Предусловие |
Постусловие |
1 |
нет |
б |
2 |
а,б |
в |
3 |
в |
г,а |
4 |
г |
нет |
Такое представление системы легко моделировать сетью Петри.
В сети Петри условия моделируются
позициями, события - переходами. При
этом входы перехода являются предусловиями
соответствующего события; выходы -
постусловиями. Возникновение события
равносильно запуску соответствующего
перехода. Выполнение условия представляется
фишкой в позиции, соответствующей этому
условию. Запуск перехода удаляет
разрешающие фишки, представляющие
выполнение предусловий и образует новые
фишки, которые представляют выполнение
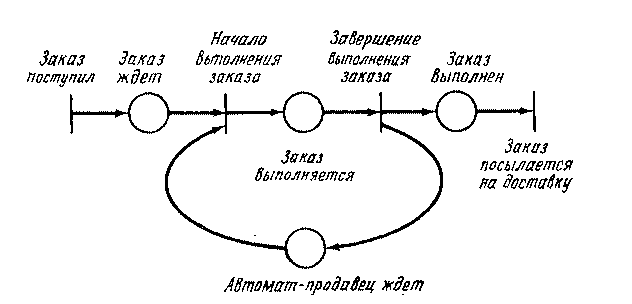
постусловий. Сеть Петри на рис. 3.1
иллюстрирует модель приведенного выше
автомата-продавца. Мы указали каждому
переходу и позиции соответствующие
событие и условие.
Можно моделировать и более сложную систему. Система автомат-продавец состоит из трех различных автоматов M1 , М2 и М3 и двух операторов F1 и F2. Оператор F1 воздействует на автоматы М1 и М2, а оператор F2 — на М1 и М3. Заказы требуют двух стадий обработки. Сначала они должны быть обработаны автоматом М1 затем либо автоматом М2 либо М3. Эта более сложная система будет иметь следующие условия:
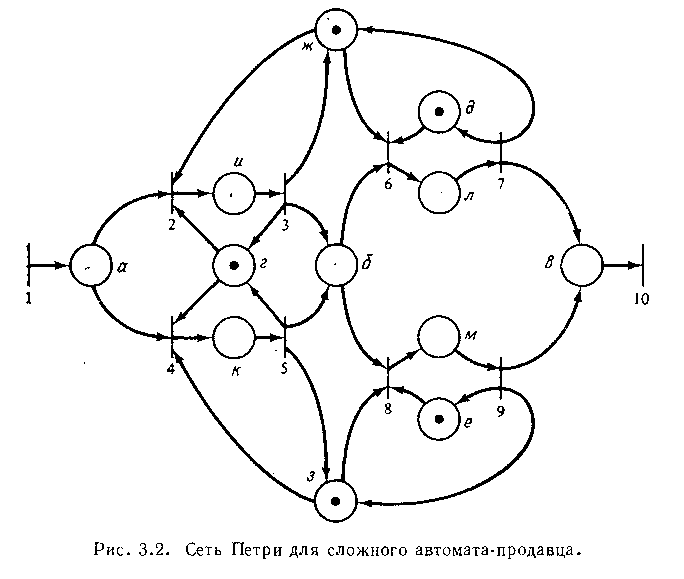
а) заказ прибыл и ждет обработки автоматом М1
б) заказ обработан автоматом М1 и ждет обработки либо автоматом М2, либо М3;
в) заказ выполнен;
г) автомат M1 незанят;
д) автомат М2 незанят;
е) автомат М3 незанят;
ж) оператор F1незанят;
з) оператор F2 незанят;
и) автомат М1 находится под воздействием оператора F1
к) автомат М1 находится под воздействием оператора F2,
л) автомат М2 находится под воздействием оператора F1,
м) автомат М3 находится под воздействием оператора F2.
При этом могут происходить следующие события:
1. Поступление заказа.
2. Оператор F1 начинает выполнение заказа на автомате M1
3. Оператор F1 закончил выполнение заказа на автомате М1.
4. Оператор F2 начинает выполнение заказа на автомате М1.
5. Оператор F2 закончил выполнение заказа на автомате М1.
6. Оператор F1 начинает выполнение заказа на М2.
7. Оператор F1 закончил выполнение заказа на М2.
8. Оператор F2 начинает выполнение заказа на М3.
9. Оператор F2 закончил выполнение заказа на М3.
10. Заказ посылается на доставку.
