49. Детерминированные меры живучести для многополюсных сетей

Отказ отдельных ребер прим. Узлов влияет на функционирование всей сети. Степень влияния зависит от того, какие элементы отказали в процессе работы сети. Математическая сеть моделируется в виде графа, поэтому выход из строя элементов – это удаление ребер или узлов графа.

Предположим, что граф неориентированный. Минимальный разряд i-j в связях графа G есть такое минимальное количество ребер, при удалении которого не остается хотя бы одного пути, соединяющего вершину I и j. Минимальное число таких ребер называется реберной связанностью между узлами I и j. (bij)

Реберная связанность графа G определяется как b(G) = min bij для всех возможных узлов I,j.

B(G) задает минимальное количество ребер с удалением которых граф распадается, нарушается связность.

Аналогично – угловая связность (-bij)

-b(G) = min –bij отказ узла равнозначен отказу всех ребер, инцидентных этому узлу. –bij относится I и j – определяется, как минимальное число узлов, удаление которых нарушает связь между узлами I и j. Узловая связанность графа G можно определить по формуле –b(G) = min –bij.

Узловая связанность графа –b(G) минимальное количество узлов с удалением которых нарушается связность графа G относительно двух вершин.

В соответствии с теоремой Менгера – величина -bij = max количеству путей между узлами I и j, которые не имеют общих ребер. Тем самым, проблема определения реберной и узловой связности сводится к определению множества соответствующих путей.

ТЕОРЕМА МЕНГЕРА: максимальное число вершин, не пересекаемся простых (минимальных) цепей, соединенные 2 различные вершины (не смежные) s и t графа G равны минимальному числу вершин в st, отделяющих подмножеств.

Мы будем исходить, что все узлы КС сети имеют равное значение для всей системы. –bij и bij – меры надёжности

ПРИМЕР: рассмотрим обобщенную связь b(G). Введем минимальное число Z(m) ребер и удалением которых какой-нибудь подграф с m узлами станет изолированным от остальных частей графа G. Сеть КС тем надежнее, чем больше возможных значений принимает z(t)

B(G) = min (Z(m)) – минимальные из m

Меры основаны на том, что работоспособность сохраняется и имеется путь между двумя узлами. Длина пути не учитывается. Хотя она играет важную роль, т.к. в очень длинных цепях могут возникать недопустимые задержки.

50. Матричная теорема о деревьях для графов (пример)

Матричная теорема о деревьях (Matrix tree theorem), также известная как Теорема Кирхгофа — теорема теории конечных графов.

Теорема Кирхгофа-Трента

Пусть   — связный помеченный граф с матрицей Кирхгофа  . Все алгебраические дополнения матрицы Кирхгофа   равны между собой и их общее значение есть число остовных деревьев графа  . Можно расширить теорему на случай мультиграфов и взвешенных графов. Тогда алгебраические дополнения элементов матрицы Кирхгофа для взвешенного графа будут равны сумме произведений проводимости всех остовов. Частный случай получается, если взять проводимости равными 1: сумма произведений проводимостей остовов будет равна числу остовов.

Пусть   обозначает матрицу, получаемую из матрицы  , где   — матрица смежности графа  , с помощью подстановки в ней на место   -го диагонального элемента числа  .

Матричная теорема о деревьях для графов. Для всякого связного помеченного графа   все алгебраические дополнения матрицы   равны друг другу и их общее значение представляет собой число каркасов графа   .

Пример. Для графа   (рис.11. 3) с матрицей смежности

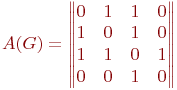
матрица   имеет вид

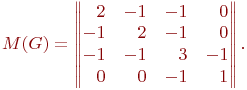
Алгебраическое дополнение, например, элемента  , равно  . Соответствующие каркасы графа   показаны на (рис.11. 4).

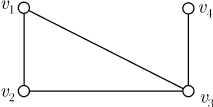
Рис. 11.3. 

Рис. 11.4. 

Интересен также следующий результат. Пусть   -вершинный граф без петель и   — его матрица инциденции с одной удаленной строкой (т.е. с   независимыми строками). Пусть   — транспонированная матрица к  . Тогда определитель   равен числу остовных деревьев графа  .