
- •Классификация параллельных кс по структурно-функциональным признакам.
- •Классификация параллельных кс по функциональным возможностям кс с точки зрения пользователя
- •Проведите сравнительный анализ классификаций компьютерных систем.
- •Мультикомпьютеры, кластеры и симметричные мультипроцессоры общая характеристика, схемы построения, особенности каждой из систем, области применения.
- •Системы с распределенной и разделяемой памятью, массово-параллельные системы общая характеристика, схема построения, особенности каждой из систем, области применения.
- •Преимущества архитектуры
- •Недостатки архитектуры
- •Основные понятия теории моделирования параллельных кс. Методы моделирования параллельных кс.
- •Задачи моделирования параллельных кс.
- •Приведите основные принципы моделирования.
- •Моделирование параллельных процессов. Применение аппарата сетей Петри.
- •Подклассы сетей Петри:
- •Применение сетей Петри для синтеза дискретных управляющих устройств.
- •Оценочные или е-сети как расширение сетей Петри
- •Моделирование конвейерной обработки информации
- •Свойства сохранения и активности сети Петри
- •Свойство достижимости и покрываемости сети Петри.
- •Свойство безопасности и ограниченности сети Петри.
- •Анализ сетей Петри матричным методом
- •Матричный метод анализа сетей Петри достоинства и недостатки метода
- •Задачи достижимости и покрываемости сети Петри.
- •Границы возможности моделирования с помощью сетей Петри
- •Подклассы сетей Петри:
- •Маркированные графы подкласс сетей Петри
- •Сети Петри и их особенности
- •Разбиения чисел. Основные понятия и определения. Принцип Дирихле.
- •Вложимость разбиений.
- •Ранговое условие вложимости; пример использования.
- •Принцип полного размещения; пример использования.
- •Вложимость с ограничениями; пример использования.
- •Особенностью распределения памяти в кс с сегментной организацией программ и данных (модель 2). Приведите пример.
- •Комбинаторная модель для оценки необходимого размера памяти кс (модель 4). Приведите пример.
- •Комбинаторная модель, позволяющая произвести расчет оценки сверху необходимого размера оперативной памяти кс.
- •Диаграммы Ферре и инверсия в бинарных последовательностях
- •Надежность кольцевой структуры кс (для сети [n,2]).
- •Надежность сети кс.
- •Связанные случайные величины
- •Детерминированные меры живучести для многополюсных сетей
- •Матричная теорема о деревьях для графов (пример)
- •Теорема Кирхгофа-Трента
- •Каркасы в ориентированных графах
- •Надежность сети относительно одного источника и многих стоков
Комбинаторная модель, позволяющая произвести расчет оценки сверху необходимого размера оперативной памяти кс.
Пусть имеется m групп
запросов на выделение памяти. Размер
j-ой группы
соответствует числу разбиений:
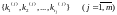
В соответствии с принципом полного
размещения можно показать, что вычислимая
величина
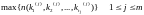 ,
при условии, что
,
при условии, что
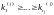 и обеспечивает нахождение суммарного
размера свободной памяти. Причем всякое
разбиение на не более, чем r
участков обеспечит полное удовлетворение
запросов на память любой группы
и обеспечивает нахождение суммарного
размера свободной памяти. Причем всякое
разбиение на не более, чем r
участков обеспечит полное удовлетворение
запросов на память любой группы
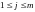 .
.
Диаграммы Ферре и инверсия в бинарных последовательностях




ИЗ СЕМИНАРОВ
Задача отображения множества программных модулей на множество процессоров
Надежность кольцевой структуры кс (для сети [n,2]).
Рассчитаем надежность кольцевой структуры:
Е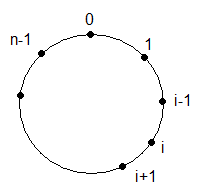 сли
занумеровать узлы кольца так, чтобы
связи между узлами задавать таблицей
пар:
сли
занумеровать узлы кольца так, чтобы
связи между узлами задавать таблицей
пар:
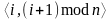 ,
то вероятность отказа связей между
узлами i и j
будет определяться зависимостью:
,
то вероятность отказа связей между
узлами i и j
будет определяться зависимостью:
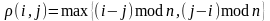 ,
при
,
при
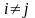 изменяется от 1 до
изменяется от 1 до
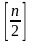 .
.
Тогда достаточно определить вероятность отказа связей между узлами 0 и i=1,2,…l=[n/2]. Между этими узлами существует 2 пути:
1:
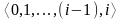 , (i-1) промежуточных узлов
, (i-1) промежуточных узлов
2:
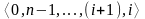 ,
n-i ребер.
,
n-i ребер.
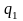 –
отказ узла,
–
отказ узла,
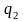 –
отказ линий связи.
–
отказ линий связи.
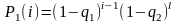 – для первого пути.
– для первого пути.
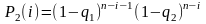 –
для второго пути.
–
для второго пути.
Вероятности
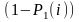 и
и
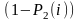 вероятности разрыва связи. Для того,
чтобы разорвать связи между узлами 0 и
I, нужно разорвать оба
пути:
вероятности разрыва связи. Для того,
чтобы разорвать связи между узлами 0 и
I, нужно разорвать оба
пути:
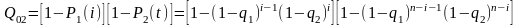 .
Дальше найдем максимум.
.
Дальше найдем максимум.
При i=l выражение достигает максимума.
При n=2l получаем выражение:
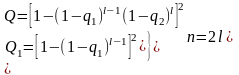
Q – это глобальная, Q1 – реберная, Q2 – узловая.(вроде так…)
Надежность сети кс.
Надежность – свойство КС выполнять любую функцию при определенных условиях эксплуатации в течение заданного времени и с установленными параметрами.
Отказ – событие, состоящее в полной или частичной утрате работоспособности КС. Наступает, когда система не сохраняет свои параметры в заданных пределах.
Основная характеристика надежности вероятность того, что при заданных условиях в течение заданного времени отказ в ней не возникнет.
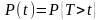 ,
где T – наработка на отказ,
t – заданное время.
,
где T – наработка на отказ,
t – заданное время.
Аналогия с функцией надежности – функция
ненадежности (вероятность отказа):
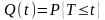 .
Из определения функции
.
Из определения функции
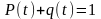 или
или
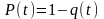 .
Если заданное время произвольное, то
тогда
.
Если заданное время произвольное, то
тогда
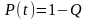 ,
следовательно мерой Р может выступать
значение Q, т.е. чем больше
Q, тем меньше надежность.
,
следовательно мерой Р может выступать
значение Q, т.е. чем больше
Q, тем меньше надежность.
Количественная надежность сети – вероятность разрушения связей сети.(?/Дальше в лекциях пробел)
КС с приводимой и неприводимой структурой
Пути и резервы двухполюсного графа
Связанные случайные величины
Оценки вероятности связного двухполюсного графа
Граничные оценки Эзари-Прошана для вероятности связного двухполюсного графа
Метод Эзари-Прошана Данный метод позволяет определить верхнее и нижнее граничные значения вероятности связности полюсов графа. Данный метод опирается на следующие положения: Если события А и В положительно коррелированы, то . Если распространить это на любое количество элементов, то .
В результате получаем: для простых разрезов. для простых цепей. - 2-стороняя оценка Эзари-Прошана. Представление произвольного 2-полюсного графа в виде параллельного соединения простых цепей, составленных из независимых элементов, дает верхнюю оценку вероятности связности. Представление этого же графа в виде последовательного соединения простых разрезов дает нижнюю оценку этой вероятности.
Пример оценки Литвака-Ушакова для мостиковой системы
Понятие о монотонной структуре в теории надежности
Граничные оценки Литвака-Ушакова для вероятности связного двухполюсного графа
Метод Литвака-Ушакова 1. Представление графа в виде параллельного соединения реберно-непересекающихся простых цепей: а) Выбираем произвольную простую цепь. Исключаем ее из графа. б) Выбираем из оставшейся части графа другую простую цепь. Исключаем ее из графа, и т.д. до тех пор пока граф не окажется несвязным или пока не будут использованы все ребра. 2. Представление графа в виде последовательного соединения реберно-непересекающихся простых разрезов: а) Выбираем произвольный простой разрез. б) Все вершины с одной стороны оттягиваем в одну точку, а все вершины с другой стороны – в другую точку. Выполняемые операции эквивалентны введению в граф “абсолютно надежных” ребер. Следовательно любой из полученных оценочных графов имеет завышенную вероятность связности. В сложных сетевых вычислительных системах аналитическое описание моделей очень громоздкое, а иногда невозможное. В этом случае производят имитацию реального процесса на статистической модели, воспользовавшись статистическими данными о параметрах системы. Недостатком данного метода является то, что он содержит избыточность приводящую к увеличению объема расчета. Некоторые реализации эксперимента можно не моделировать. Если не работают 1 или 2, то нет необходимости моделировать 3,4,5. если работает 1 и 4, то нет необходимости моделировать 5, т.к. есть уже простая цепь.
Пример оценки Литвака-Ушакова для мостиковой схемы
Сравнение оценок Эзари-Прошана с оценками Литвака-Ушакова
