28. Ранговое условие вложимости; пример использования.

Иногда удается решить комбинаторную задачу распознавания вложимости разбиений без алгоритмической проверки.Существуют теоремы для выяснения вопроса вложимости некоторых фиксированных разбиений.

Теорема.

Пусть t является тем наименьшим t, при котором 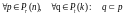, тогда .

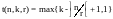Следствие: если 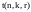- наименьшее n, при котором 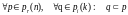, то

29. Принцип полного размещения; пример использования.

Пусть 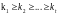и дано r, все – натуральные числа. Наименьшее 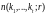, при котором разбиение к вложимо в разбиение этого n на не более чем r частей.

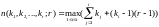
Следствие: если для натуральных чисел 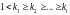выполнено условие 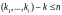и через 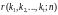обозначено наибольшее r, при котором каждое разбиение r на n частей вложимо в разбиение 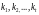, то

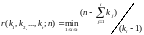
Искомое r согласно принципу полного размещения есть необходимый целый корень неравенства

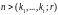
30. Вложимость с ограничениями; пример использования.

Иногда требуется гарантировать вложимость разбиения не во все разбиения чилс n на r частей, а только в некоторые. Экстремальный результат, гарантирующий вложимость фиксированного разбиения уже не во все разбиения данного ранга можно представить в виде следующего утверждения:

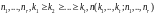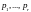пусть - наименьшее n при котором каждое разбиение этого n на r частей такое, что 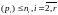, обладает тем свойством, что 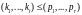, тогда .

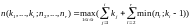В отличие от принципов полного размещения, последнее утверждение обеспечивает не только установление факта вложимости разбиений, но и для некоторых разбиений может использоваться как условие невложимости.

31. Комбинаторные модели для исследования процесса распределения памяти

32. Особенностью распределения памяти в кс с сегментной организацией программ и данных (модель 2). Приведите пример.

Особенностью распределения памяти КС с сегментной организацией программ и данных является неделимость поступающих запросов на выделение памяти. Т.е. для удовлетворения каждого запроса требуется непрерывный участок адресного пространства различной длины.

Такая организация распределения памяти применяется в системах телеобработки данных при распределении ОП в многопроцессорных вычислительных комплексах.

Удовлетворение любого запроса на память реализуется последовательным выполнением 2 процессов:

- процесса поиска непрерывных участков адресного пространства не меньшего, чем размер запроса;

- процесса выделения свободной памяти под запрос.

В соответствии с определением вложимости разбиения, вложимо в разбиение , если части разбиения можно так сгруппировать в r-групп, что после сложения всех частей в каждой группе получится r-чисел : .

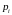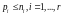В процессе конкретной вложимости 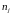из разбиения используется не более одного раза.

Понятие вложимости разбиений является интерпретацией процесса удовлетворения запросов свободной памяти КС.

33. Комбинаторная модель для оценки необходимого размера памяти кс (модель 4). Приведите пример.

Размер оперативной памяти оказывает влияние на функционирование КС. Увеличение ОП повышает производительность КС без каких-либо изменений программ обработки.

При проектировании КС вопросу оценки КС уделяется большое внимание на всех этапах проектирования. Проведение таких исследований требует существенных затрат и ресурсов, и увеличивает время создания системы.

При пиковых нагрузках КС должна оставаться работоспособной.

Эффективное функционирование КС невозможно без выполнения условия: в результате проектирования ПО должно соответствовать аппаратуре. Оно должно быть спроектировано так, чтобы не снижать производительность аппаратной части и всей системы в целом. Используя подходы для решения задачи распределения памяти можно получить такое решение этой задачи, которое проявится только на этапе эксплуатирования системы. Для решения задачи управления распределением данных используется ряд комбинаторных моделей. Последовательность представления таких моделей можно выбрать в соответствии с количеством априорной информации о процессе функционирования ОП КС.

Рассматривается функционирование КС, в которой запросы на выделение памяти поступают группами. Пусть размеры запросов группы поступившей в произвольный момент времени соответствуют 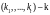. Свободная память рассматривается как r участков с суммарным размером n. Тогда согласно принципу полного размещения

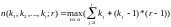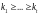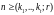, . Следовательно, что для решения подобной задачи не требуется информация по размерам свободных участков памяти. Достаточно проверить: , r – количество фрагментов свободной памяти.