
- •Классификация параллельных кс по структурно-функциональным признакам.
- •Классификация параллельных кс по функциональным возможностям кс с точки зрения пользователя
- •Проведите сравнительный анализ классификаций компьютерных систем.
- •Мультикомпьютеры, кластеры и симметричные мультипроцессоры общая характеристика, схемы построения, особенности каждой из систем, области применения.
- •Системы с распределенной и разделяемой памятью, массово-параллельные системы общая характеристика, схема построения, особенности каждой из систем, области применения.
- •Преимущества архитектуры
- •Недостатки архитектуры
- •Основные понятия теории моделирования параллельных кс. Методы моделирования параллельных кс.
- •Задачи моделирования параллельных кс.
- •Приведите основные принципы моделирования.
- •Моделирование параллельных процессов. Применение аппарата сетей Петри.
- •Подклассы сетей Петри:
- •Применение сетей Петри для синтеза дискретных управляющих устройств.
- •Оценочные или е-сети как расширение сетей Петри
- •Моделирование конвейерной обработки информации
- •Свойства сохранения и активности сети Петри
- •Свойство достижимости и покрываемости сети Петри.
- •Свойство безопасности и ограниченности сети Петри.
- •Анализ сетей Петри матричным методом
- •Матричный метод анализа сетей Петри достоинства и недостатки метода
- •Задачи достижимости и покрываемости сети Петри.
- •Границы возможности моделирования с помощью сетей Петри
- •Подклассы сетей Петри:
- •Маркированные графы подкласс сетей Петри
- •Сети Петри и их особенности
- •Разбиения чисел. Основные понятия и определения. Принцип Дирихле.
- •Вложимость разбиений.
- •Ранговое условие вложимости; пример использования.
- •Принцип полного размещения; пример использования.
- •Вложимость с ограничениями; пример использования.
- •Особенностью распределения памяти в кс с сегментной организацией программ и данных (модель 2). Приведите пример.
- •Комбинаторная модель для оценки необходимого размера памяти кс (модель 4). Приведите пример.
- •Комбинаторная модель, позволяющая произвести расчет оценки сверху необходимого размера оперативной памяти кс.
- •Диаграммы Ферре и инверсия в бинарных последовательностях
- •Надежность кольцевой структуры кс (для сети [n,2]).
- •Надежность сети кс.
- •Связанные случайные величины
- •Детерминированные меры живучести для многополюсных сетей
- •Матричная теорема о деревьях для графов (пример)
- •Теорема Кирхгофа-Трента
- •Каркасы в ориентированных графах
- •Надежность сети относительно одного источника и многих стоков
Сети Петри и их особенности
Def.Сеть Петри – четверка С=(P,T,I,O), где P – множество позиций, T – множество переходов, I – является входной функцией (отображением из переходов в комплекты позиций), O – выходная функция (отображения из переходов в позиции).
Сети Петри – инструмент исследования систем. Теория сетей Петри делает возможным моделирование системы математическим представлением ее в виде сети Петри. Предполагается, что анализ сети Петри поможет получить важную информацию о структуре и динамическом поведении моделируемой системы.
Возможно несколько подходов к использованию сетей Петри при проектировании и анализе ВС:
Сеть Петри можно рассматривать как вспомогательный инструмент, т.е. для построения ВС используются общие принципы проектирования, затем построенная система моделируется сетью Петри и производится анализ полученных результатов. Любые нестыковки, встречающиеся при анализе сети Петри, указывают на недоработки при проектировании. Для их исправления необходимо модифицировать проект.
Весь процесс проектирования и определения параметров ВС проводится в терминах сетей Петри. Задача сводится к представлению сетью Петри реальной рабочей системы.
Понятие о топологическом синтезе и анализе структур КС.
Разбиения чисел. Основные понятия и определения. Принцип Дирихле.
Разбиение натурального числа n,
есть его представление неупорядоченной
суммой натуральных слагаемых:
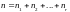 .
Эти слагаемые
.
Эти слагаемые
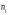 и называются частями, а их число r
– рангом разбиения.
и называются частями, а их число r
– рангом разбиения.
Композиция – это представление натурального числа n упорядоченной суммой натуральных слагаемых
n=6
ранг 1: 6=6;
ранг 2: 6=5+1, 6=4+2, 6=3+3;
ранг 3: 6=4+1+1, 6=3+2+1, 6=2+2+2;и т.д.
ранг 6: 6=1+1+1+1+1+1;
Как найти число композиций натурального числа n=r? Это будет число способов, которыми можно разместить r-1 черточек между n-1 промежутками.
если ранг не фиксировать, то черточку
в каждом из промежутков можно как
поместить, так и не поместить. Наибольшее
число композиций будет равно
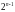 .
Т.о. композиции можно понимать как
упорядоченное или неупорядоченные
мультимножества, элементы которых
являются натуральными числами.
.
Т.о. композиции можно понимать как
упорядоченное или неупорядоченные
мультимножества, элементы которых
являются натуральными числами.
Разбиение изображают при помощи векторной
записи:
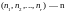 .
.
или в сокращенной записи:
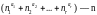
Часть
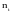 присутствует в разбиении
присутствует в разбиении
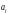 раз, т.о.
раз, т.о.
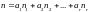
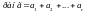
Всякое разбиение можно представить в
виде
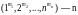 ,
где
,
где
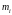 - целое, неотрицательное число, которое
указывает сколько раз число i
присутствует в этом разбиении в виде
части
- целое, неотрицательное число, которое
указывает сколько раз число i
присутствует в этом разбиении в виде
части
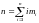 (
(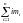 -ранг
разбиения). Разбиение можно изобразить
графически, с помощью графа Ферре
(Ферррер)
-ранг
разбиения). Разбиение можно изобразить
графически, с помощью графа Ферре
(Ферррер)
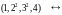

Принцип Дирихле.
Если
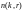 является наименьшим целым n,
при котором в каждом разбиении этого n
на r частей, найдется
часть не меньшая, чем k,
то тогда
является наименьшим целым n,
при котором в каждом разбиении этого n
на r частей, найдется
часть не меньшая, чем k,
то тогда
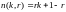
Принцип Дирихле можно сформулировать в виде размещения (принцип ящика):
при любом размещении r+1 предметов по r ящикам, то найдется ящик с двумя предметами.
Вложимость разбиений.
Основным соответствием между разбиениями
чисел является их вложимость, т.е.
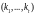 входит в разбиение
входит в разбиение
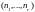 ,
если существует отображение
,
если существует отображение
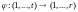 ,
при котором выполняется система
неравенств:
,
при котором выполняется система
неравенств:
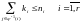 ,
где
,
где
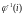 - полный прообраз элемента i
при отображении
- полный прообраз элемента i
при отображении
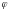 .
.
Каждая часть
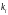 входит в одну группу; пустые группы
исключаются.
входит в одну группу; пустые группы
исключаются.
Если разбиение
вложимо в
,
то будем записывать это, используя
обозначение включения множеств:

Элементарные свойства разбиений:
каким наиб быстрым способом можно определить вложимость?
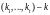 ,
,
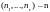
Если выясняется, что
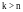 ,
то k не вложимо во второе.
Это утверждение лежит в основе
экстремального подхода к построению
быстрого способа проверки вложимости.
,
то k не вложимо во второе.
Это утверждение лежит в основе
экстремального подхода к построению
быстрого способа проверки вложимости.
