Границы возможности моделирования с помощью сетей Петри
Дейкстра определил свои Р- и V-операции над семафорами для обеспечения синхронизации и связи в системах взаимодействующих процессов [78]. Семафор может рассматриваться как целочисленная переменная, которая принимает только отрицательные значения.
V-операция над семафором S увеличивает значение семафора на единицу: S = S + 1. Р-операция, наоборот, уменьшает S на едиединицу до тех пор, пока результат не становится равным нулю; при S = 0 процесс, прежде чем продолжать свою работу, должен ждать момента, когда S можно будет уменьшить. Связь между семафорами и сетями Петри была выявлена в разд. 3.4.8.
Поскольку Р- и V-операции были предложены как механизм для решения всех задач синхронизации программ, то естественно возникает вопрос о полноте, т. е. об их способности к решению всех задач координации. Патил в 1971 г. [233] предложил доказательство того, что Р- и V-операции недостаточно мощное средство для решения всех задач координации. Его подход был весьма прост: он сформулировал задачу синхронизации, которая не может быть решена с помощью Р- и V-операций, — это задача о курильщиках сигарет.
Задача о курильщиках сигарет включает (по меньшей мере) четыре процесса, которые моделируют агента и трех курильщиков. Каждый курильщик непрерывно изготавливает сигарету и курит ее. Чтобы сделать сигарету, необходимы три составные части: татабак, бумага и спички. Один из курильщиков всегда имеет бумагу, другой — табак, а третий — спички. Агент обладает бесконечными запасами всех трех составных частей. Агент кладет две составные части на стол. Курильщик, имеющий третий недостающий, может сделать и закурить сигарету, сигнализируя об этом агенту. Тогда агент помещает другие два из трех инградиентов, и цикл повторяется.
Если семафор поставить в соответствие каждой составной части, задача о курильщиках формулируется в терминах семафоров. Семафоры первоначально равны нулю. Агент увеличит два из трех семафоров с помощью V-операций, а затем ждет семафора «сделано».
Соответствующий процесс курильщика уменьшает два семафора (с помощью Р-операций), а затем, произведя действия «сделать сигарету» и «закурить сигарету», увеличивает семафор, указывая «сделано». Задача заключается в том, чтобы разработать программу процессов курильщиков для того, чтобы определить, какой из трех процессов должен действовать в очередной момент. Действия агента фиксированны и не могут быть изменены.
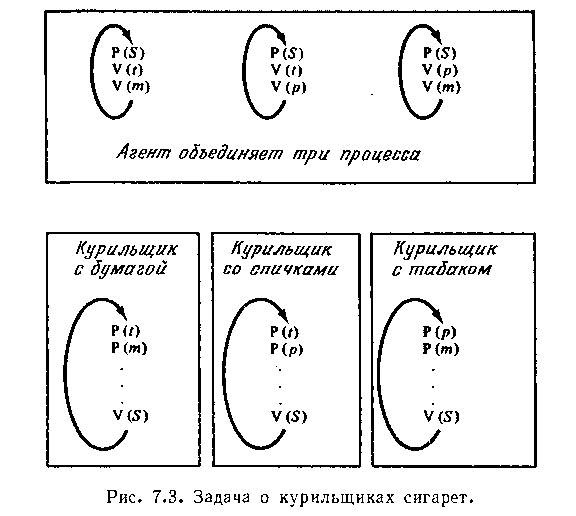
Рис. 7.3 иллюстрирует очевидное «решение». Предположим, агент кладет табак и бумагу [V(t), V(p)].
Тогда курильщик с бумагой может взять табак [P(t)], а курильщик с табаком может взять бумагу [Р(р)], что в результате приводит к тупику. Патил доказал, что никакая последовательность Р- и V-операций не может корректно решить эту задачу. Это было показано с помощью доказательства того, что все Р- и V-«peшeния» могут быть промоделированы сетями Петри определенного вида (каждый переход имеет не более двух входов), но что решением является сеть Петри другого вида, и нет способа преобразовать сеть одного вида в сеть другого вида, не допуская возможности возникновения тупика.
Более конкретно ограничение на
моделирование с помощью сетей Петри
состоит в неспособности проверить на
наличие точно определенной маркировки
в некоторой неограниченной позиции и
осуществить действие в зависимости от
результатов проверки. Это ограничение
общеизвестно как неспособность к
проверке на нулевую маркировку в
некоторой позиции, и поэтому это свойство
известно как проверка на нуль [150]. Сети
Петри не могут проверить неограниченную
позицию на нуль. [Если позиция ограниченна,
то нуль может быть выявлен. Для ограниченной
позиции pi с границей k мы можем создать
дополнительную позицию рi
— такую, что сумма
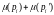является константой, равной k для всех
достижимых маркировок. Это позволяет
нам проверить, равняется ли
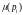нулю, проверяя, равно ли
k (см. разд. 5.6).]