18. Анализ сетей Петри матричным методом

Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Альтернативным по отношению к определению сети Петри в виде (Р, T, I, O) является определение двух матриц D⁺ и D^-, представляющих входную и выходную функции. (Они эквивалентны функциям F и В определения Хэка сетей Петри, см. разд. 2.6.) Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим D^-[j,i]= 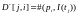, a 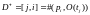, D^- определяет входы в переходы, D+ — выходы.

Матричная форма определения сети Петри (Р, T, D^- , D+) эквивалентна стандартной форме, используемой нами, но позволяет дать определения в терминах векторов и матриц. Пусть e[j] — m-вектор, содержащий нули везде, за исключением j-й компоненты. Переход tj представляется m-вектором e[j]²). Теперь переход tj в маркировке μ разрешен, если μ > e[j] • D^-, а результат запуска перехода tj в маркировке μ записывается как

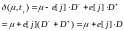
D- составная матрица изменений, тогда для последовательности запусков 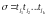имеем

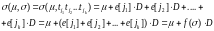
Вектор 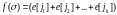называется вектором запусков последовательности 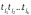i-и элемент вектора 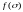, 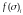— это число запусков перехода t_i в последовательности . Вектор запусков, следовательно, является вектором с неотрицательными целыми компонентами.

19. Матричный метод анализа сетей Петри достоинства и недостатки метода

Для того чтобы показать полезность такого матричного подхода к сетям Петри, рассмотрим, например, задачу сохранения: является ли данная маркированная сеть Петри сохраняющей? Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть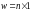 — вектор-столбец. Тогда, если — начальная маркировка, а ' — произвольная достижимая маркировка, необходимо, чтобы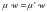 . Теперь, поскольку ' достижима, существует последовательность запусков переходов а, которая переводит сеть из в '. Поэтому 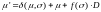Следовательно, 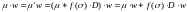, поэтому .

Поскольку это должно быть верно для всех , имеем 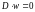. Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор w, что D • w = 0. Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания w. Развитая матричная теория сетей Петри является инструментом для решения проблемы достижимости. Предположим, что маркировка ' достижима из маркировки . Тогда существует последовательность (возможно, пустая) запусков переходов а, которая приводит из к '. Это означает, что является неотрицательным целым решением следующего матричного уравнения для х: 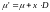. Следовательно, если достижима из тогда уравнение имеет решение в неотрицательных целых; если уравнение ) не имеет решения, тогда ' недостижима из .

20. Задачи достижимости и покрываемости сети Петри.

Задача достижимости. Для заданной сети Петри C с маркировкой и маркировки определить, верно ли, что .

Задача достижимости является одной из важнейших при анализе сетей Петри. Многие другие задачи анализа можно сформулировать в ее терминах.

Для сети Петри с рис. 4.6 тупик может возникнуть, если достижимым является состояние (0, 1, 0, 0, 0, 0, 1, 0).

Задача покрываемости. Для данной сети Петри C с начальной маркировкой и маркировки определить, существует ли такая достижимая маркировка , что .