21. Лишок нескінченно віддаленої точки.
f(z)
- аналітична в {R<|z|<
}
- ряд Лорана
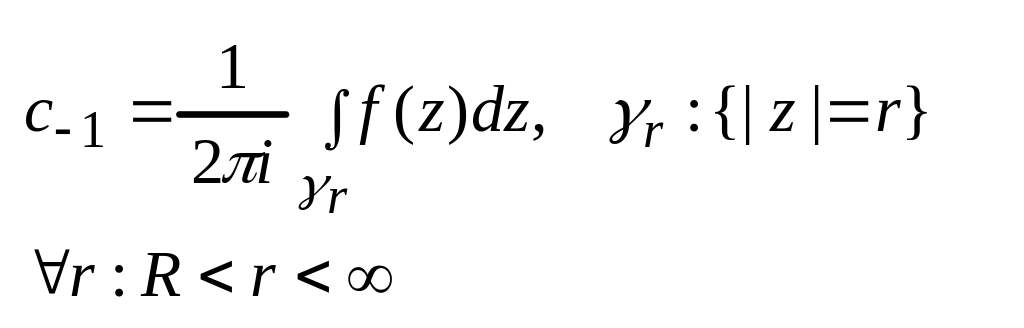
Функція для обчислення лишка нескінченно віддаленої точки не існує.
Треба розкласти функцію в ряд Лорана.....
Частный случай
- нуль
порядка т
ф-ии
,
тогда
представима
в виде:
,
где
-
анал в т
и
т
не
явл нулем ф-ии
.
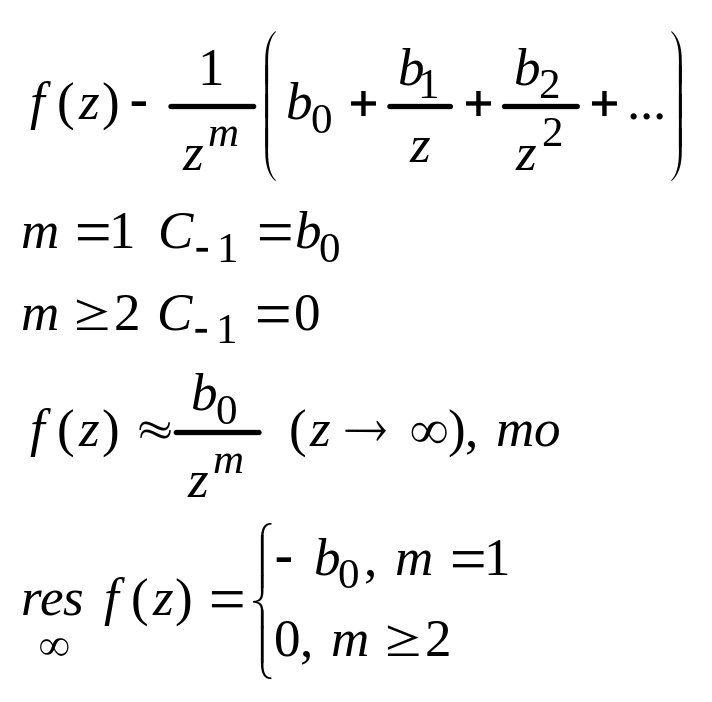
22. Основная теорема теории вычетов:
Пусть
явл
анал в односвязной обл
за
исключением конечного числа изолированных
особых точек. Пусть
- простая замкн кривая в D
и содержащая внутри себя изол особ точки
Док:
Пусть
.
Пусть
к
– такие окр, что они не пересек и лежат
в .
G
– многосвязн область. Ее граница сост
из
с выколотыми обл
,
кот обозначим как Г. По теор Коши:
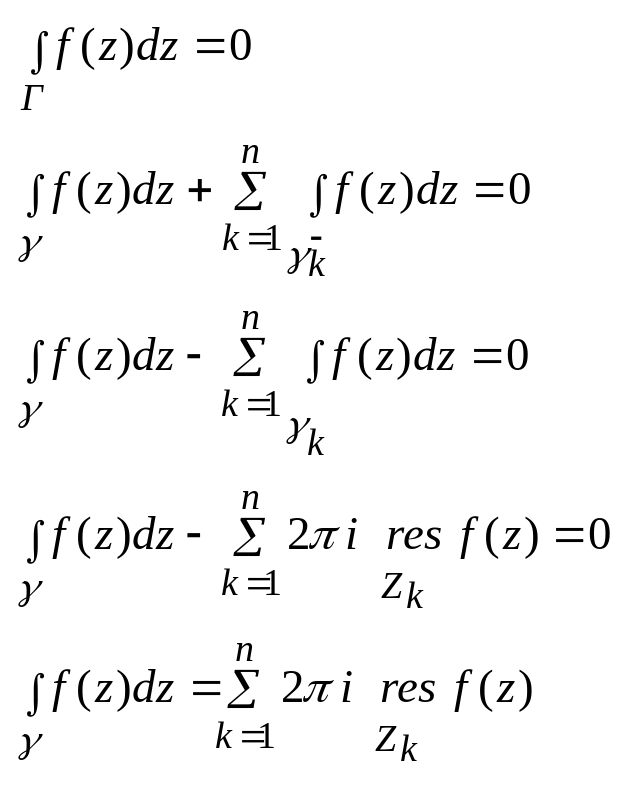
Следств: Если
-
анал в С, за исключен
изолиров особ точек
и т
.
Тогда:
Док: Пусть
число
столь
велико, что т
наход
внутри окружности
По осн теор вычетов
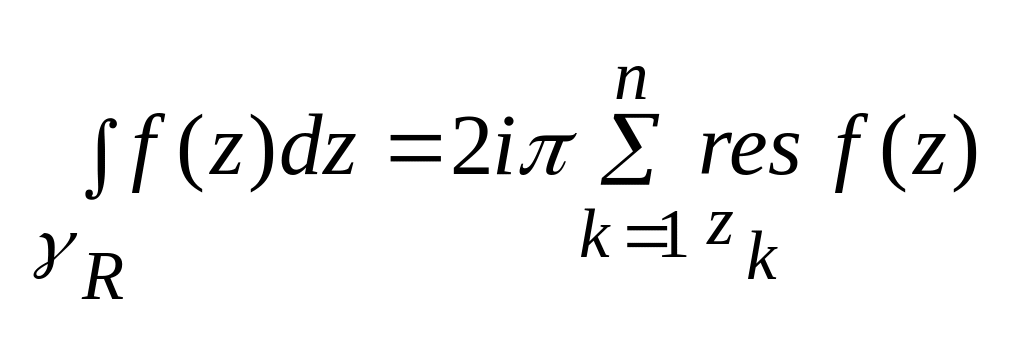
С др стороны,
из определения вычета в т
Складывая эти 2 равенства получим
23. Застосування теореми про лишки.
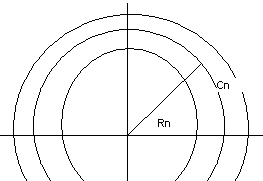
Лема Жордана.
Лема. Нехай на послідовності
визначена {Cn}(Imz>-an,
Rn→∞)
визначена ф-ція g(z)
яка прямує до 0 коли z=Rn→∞
рівномірно відносно аргумента z
(arg z).
Тоді для б-якого k>0
виконується
1. Поняття компл числа. Операції Над компл. Числами
2. Інтерпретація Рімана кч. Поняття поширеної комплексної площини.
3. Послідовність КЧ. Поняття границі.
4. Поняття фкз. Вл-ті границі. Вл-ті непер ф-ій
5. Умови Коші-Рімана диференційованості ф-ї в точці
6. Елементарні ФКЗ
7. Інтеграл від функції комплексного змінного
8. Інтегральна теорема Коші для однозв’язної області.
9. Розповсюдження інтегральній теореми Коши на випадок багатозв’язній області.
10. Інтегральна формула Коші
11. Лемма Шварца
13. Степенные ряды.
14. Ряд Лорана.
15. Усувна особлива точка(УОТ)
16. Істотно особлива точка(ІОТ)
17. Теорія лишків(теория вычетов)
18. Обчислення лишків в простому полюсі
19. Обчислення лишків в кратному полюсі
20. Обчислення лишків в істотно особливих точках
21. Лишок нескінченно віддаленої точки.
22. Основная теорема теории вычетов
23. Застосування теореми про лишки.
Лема Жордана.