13. Степенные ряды.

Т1: если функ. ряд состоит аналитичных из ф-ций (n-0,1,2…) в односвязной области Д и этот ряд равномерно сходится в Д, то его сумма тоже аналитична в Д.

T2: произвольный функ. ряд (1) члены которого - ф-ции аналитические в Д и непрерывны в замкнутой , можно в Д почленно дифференцировать бескон. кол-во раз, если этот ряд в сходится равномерно.

Т3: если степенной ряд сходится в точке , то он сходится в любой точке , которая удовлет. условию причем в области где ряд (2) сходится равномерно.

Если -- радиус сходимости.

Т4: сумма произвольный степ. ряд (2) яв. рядом Тейлора своей суммы. определена в некот. окрес-ти т. и аналит. в ней. Кроме того , тогда согласно с теоремой про разложение ф-ции в ряд Тейлора имеем , где показатель степени называется порядком нуля ф-ции в т. . порядок нуля опред. порядок первой производной, которая в т. не равна 0. Ф-цию (анал-ю) для которой можно записать в виде где -кратность (порядок) нуля, - ф-ция аналитическая: .

Т6: пусть ф-ция аналит. в окрестности т. , где она =0( ) , тогда существует достаточно малая окрестность т. в котором ф-ция не имеет других нулей кроме .

Т7: аналитичны в Д и их значения сходятся на некоторой п-ти , где а-внутр. точка Д, то .

14. Ряд Лорана.

Пусть ф-ция не будет диф. в точке , но она аналит. в об-ти где .

Например

Построим в области аналит. ф-ции две окружности радиусами . Согласно интегральной ф-ле Коши .

. если

если

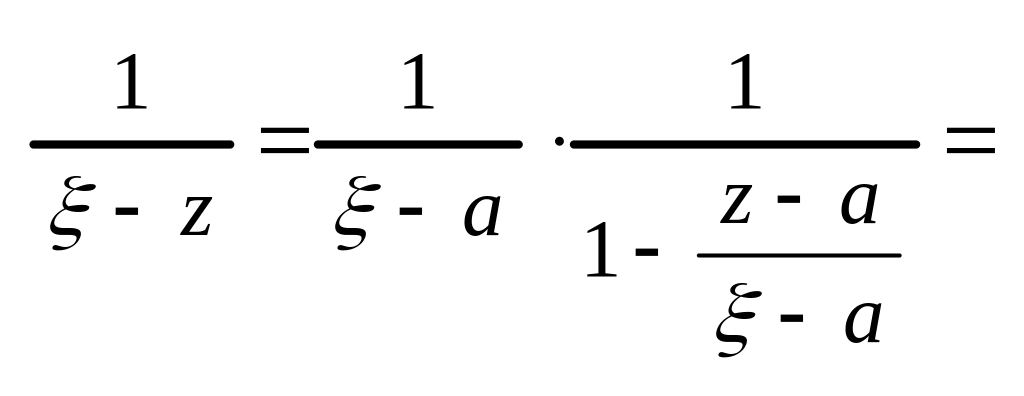
I

Домножим (4) на и проинтегрируем по в положительном направлении; получим

- ,

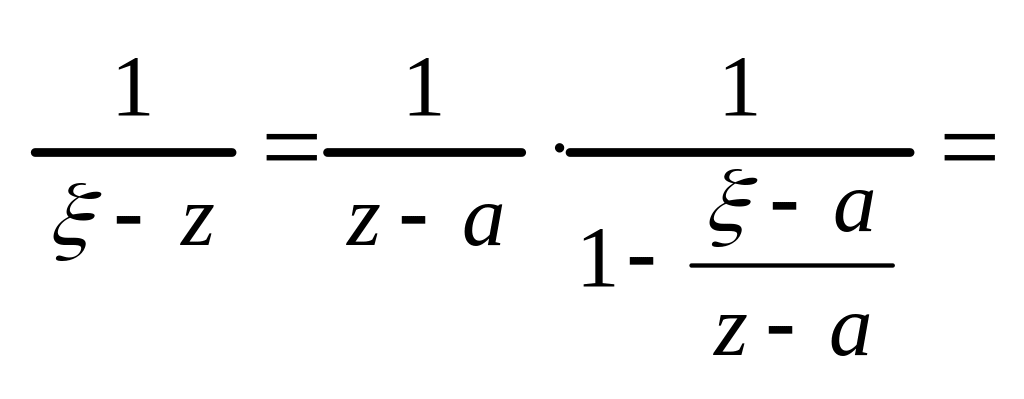
(6) и (9) можно объединить

а линия - окружность расположенная в областях аналит. . Подставим (6) и (9) в (1) получим . Ряд (5) будем называть частью ряда Лорана а ряд (8) главной частью ряда Лорана. Если аналит. в , то из (10)

и получим ряд Тейлора.

Теорема Лорана: в любом кольце в котором аналит. эта ф-ция может быть разлоена в (11) и этот ряд сходится равномерно в любой замкнутой области, что принадлежит кольцу. как для ряда Тейлора для ряда Лорана вып.:

Если (12) сходится в кольце то его сумма аналитична в кольце, а само (12) яв. рядом Тейлора этой суммы

13. Особенные точки ф-ции.

Опред. т. будем называть особенной точкой , если в этой точке ф-ция не диф.

Опред. т. наз. изолированной точкой, если в достаточно малой окрестности этой точки нет больше особенных точек.

Особ. изол. точка наз. устранимой, если . Изолированная особая точка наз. полюсом если .

Изолир. особ. точка наз. существенно особ. точкой ф-ции , если .

15. Усувна особлива точка(уот)

Нехай функція f(z) визначена в деякому околі т. а , і ця т. а - усувна особлива точка функції f(z), тобто в достатньо малому околі т. а

0<|z-a|<r – цей окіл можна розглядати як круг. Функція f(z) аналітична, і згідно з озн. особл. усувної точки

Теор: для того, щоб т.а для функції f(z) була усувною особл. точкою необх. і дост. щоб ряд Лорана для цієї ф- ії в околі т.а не мав головної частини, тобто

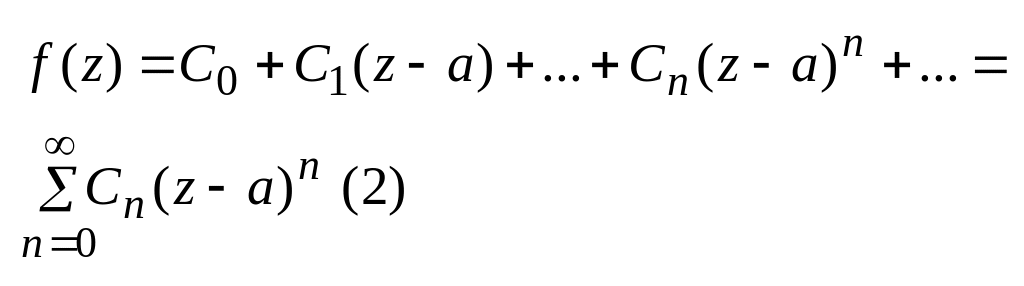
Дов: дост. нехай ряд Лорана ф-ції f(z) в околі т.а має вигляд (2) тоді

=>а – основна усувна точка

необх.: нех т.а – УОТ ф-ції f(z) тобто вик. рівн (1). За власт. ф-цій що мають скінч. границю в достатньо малому околі т.а ф-ція f(z) обмежена, тобто в цьому околі

розкладемо f(z) в околі т.а в ряд Лорана

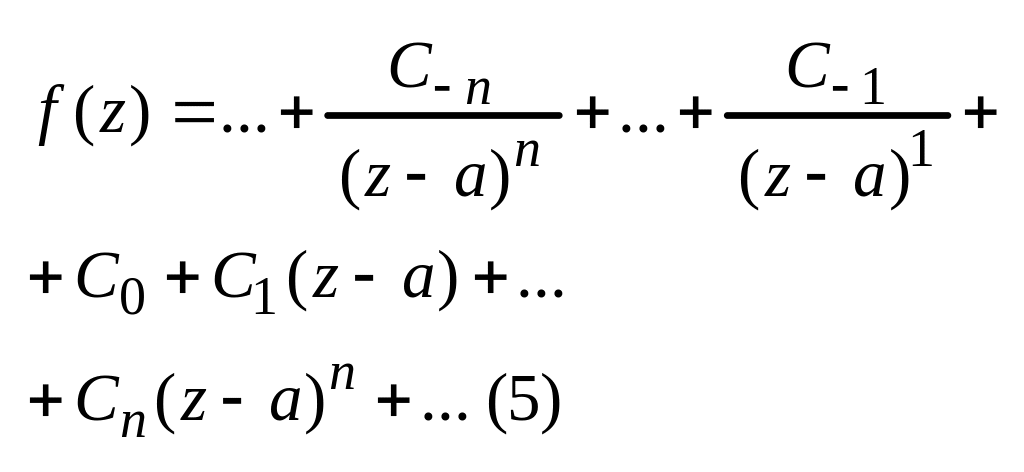
застосуємо нерівності Коші для того, щоб довести що всі коефіціенти з від’ємними номерами = 0

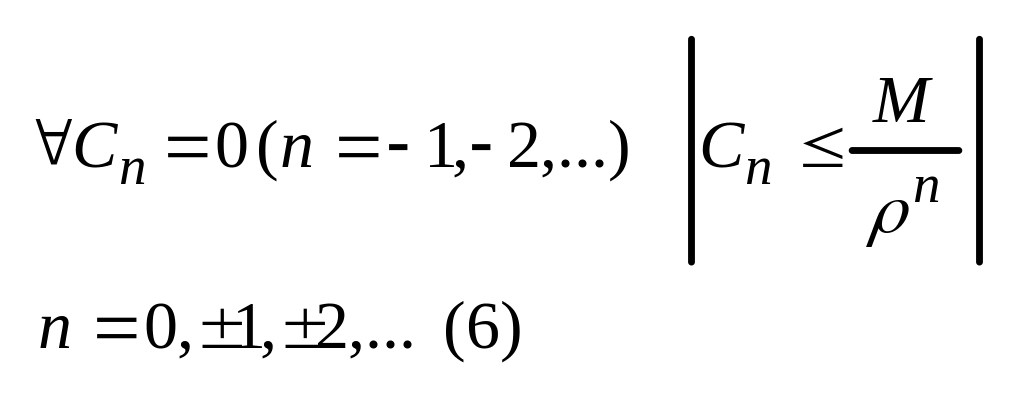
де М додатня константа, що обмежує зверху множину модулів значень функцій в околі

=|z-a|, якщо n<0 то права частина (6)

це можливо, тільки якщо C_n = 0, n=-1,-2,-3 ... тобто в Лоранівському розкладанні ф-ції f(z) в околі т.а головна частина = 0.

Зауваж. якщо покласти, що в т.а f(а) = С₀ – це коеф. ряда Лорана (5), то в достатньо малому околі т.а (включно) f(z) буде аналітична.