Теорема про середнє значення

Т.: Якщо аналітична в середині круга з центром в т. і радіусом R, і неперервна в межі круга. То значення ф-ції в т. дорівнює середньому арифметичному значення, що набуває ф-ція в т. кола, що обмежує круг: (1)

Дов.: За теоремою Коші

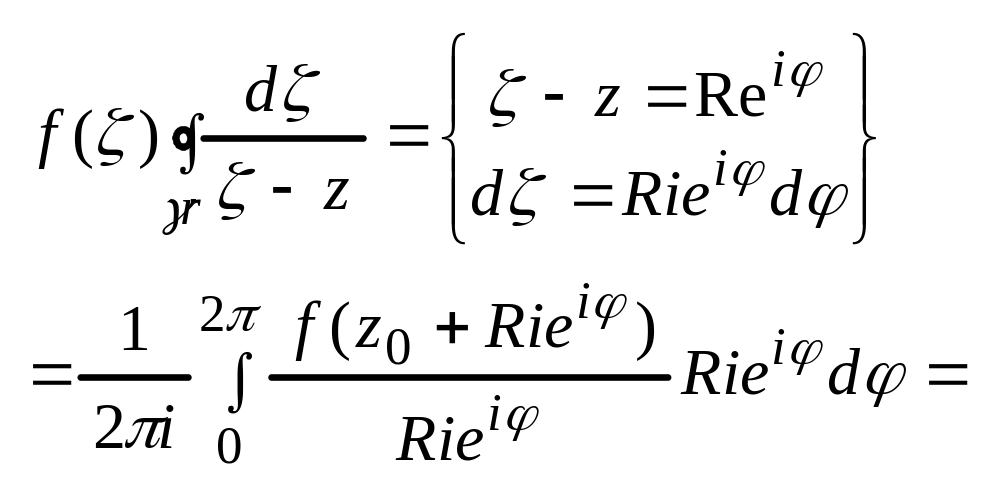
Принцип максимума

Л.: Нехай - аналітична в D. Якщо:

1) в D;

2) в D;

то ф-ція набуває сталі значення в обл. D.

Дов.: За умовами аналітична в обл. D, тобто вик. умови Коші-Рімана:

(1)

За умовами в D.

Тобто в D.

,

Нехай , ф-ція також аналітична в D, як суперпозиція двох ф-цій.

- дійсна частина в D. Звідси в D.

Т. (Принцип максимума).

Якщо аналітична в D і неперервна в та набуває в цій області стале значення, то може набувати макс. значення тільки на межі .

Висновок: Якщо аналітична в D і неперервна в і , то за умови, що у найменше значення набуває на межі обл. .

11. Лемма Шварца

Якщо ф-ція аналітична в обл. і неперервна в , причому та , то:

1.

2. Якщо принаймні в 1 т-ці цієї обл. , то це можливо тільки коли , де .

Т1: Гранична ф-ція послідовності неперервних ф-цій, яка рівномірно збігаєцця в обл. D ( на лінії С) також буде непер ф-ією

Т2: Якщо ф-ціональний ряд в обл. D посилюється числовим рядом та , та якщо числовий ряд збіг., то ф-ціональний ряд в обл. D збігається рівномірно.

Т3: Якщо послідовність неперервних ф-цій на лінії С рівномірно збігається до гран. ф-ції , то

Т4: Якщо аналітична по z і Кусково неперервна по , то для всіх z одновз’язної обл. D і всіх , збіг. в D відносно , то аналітична в D.

Вищі похідні.

Т1.: Якщо функція аналітична в D і неперервна в , то в кожній точці цієї обл. вона має похідні пор-ку, причому:

(1), С – обмежує D.

Ця теорема узагальнює формулу Коші.

Висн.: Якщо неперервна на С, що обм. обл. D, то ф-ція (2) – аналітична в області D.

Якщо вик. умови Т1, то (3)

Де - центр, а - радіус кола, яке обмежує область, що цілком складається з точок D.

Т2 (Ліувілля): Якщо в усій компл. площині і обмежена, то вона набуває стале значення в цій компл. площині.

Т3: Якщо ф-ція аналітична в усій компл. площині і її модуль зростає не швидше ніж , де , де .

Т. (Морера): Якщо ф-ція непер. в D, , по контуру С, що належить D. То аналітична в D.

12.Ряд Тейлора.

Як відомо сума членів геом прогресії 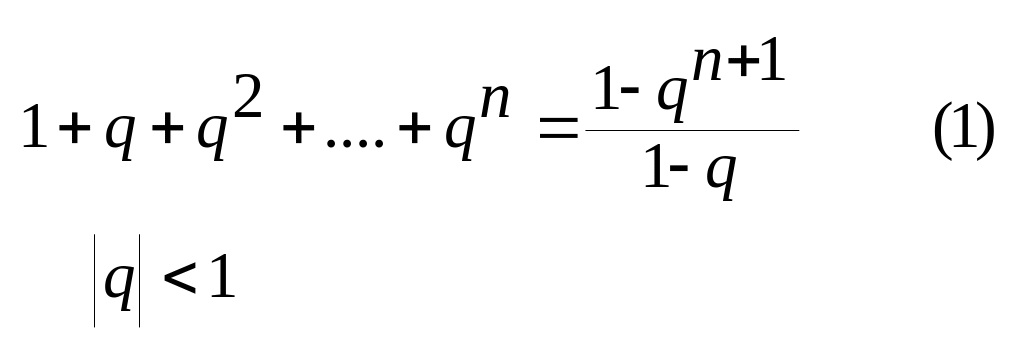. Розглянемо комплексну площину. Нехай точка а – деяка точка цієї компл площини і нехай в деякому околі цієї точки визначена аналітична ф-ція f(z). Розглянемо коло (познач С) з центром в точці а і радіусом R яке цілком належить околу т а в якому визначена аналітична ф-ція f(z). Розглянемо ф-цію де z – будь-яка точка що задовольняє умову 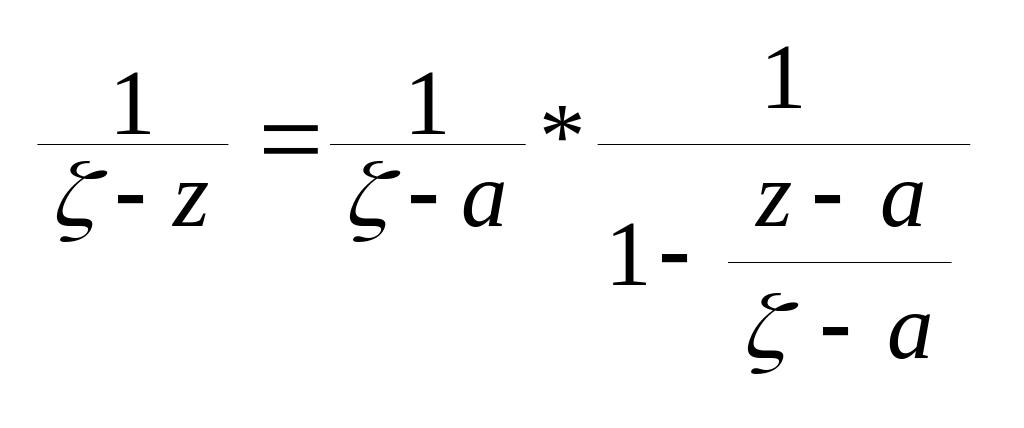зауважимо що позначимо 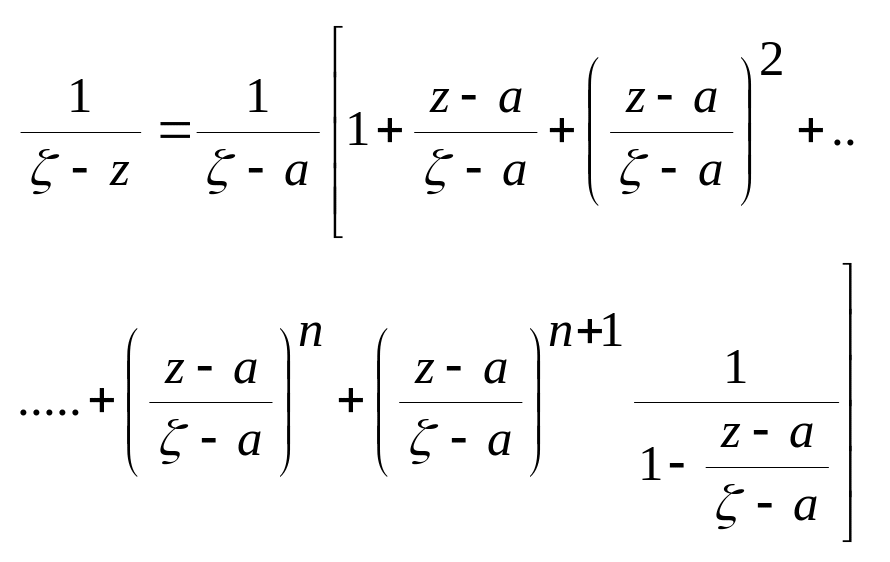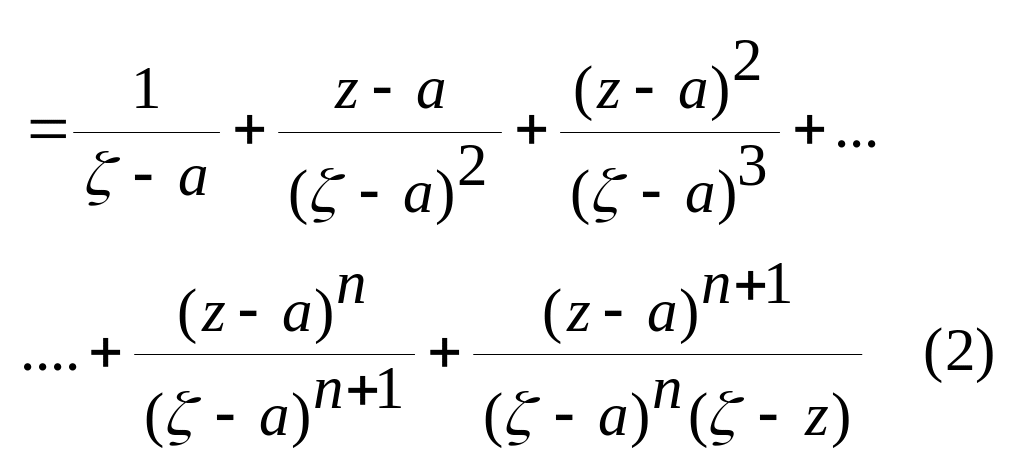. 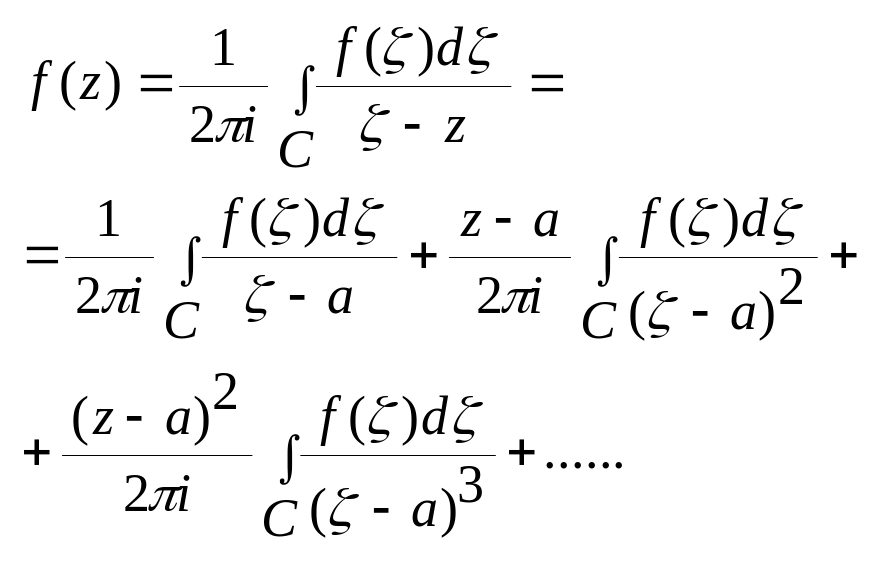Домножимо обидві частини рівності (2) на і проінтегруємо по по лінії С отримаємо де

залишковий член в загальному вигляді. Застосуємо ф-лу Коші і ф-лу вищих похідних

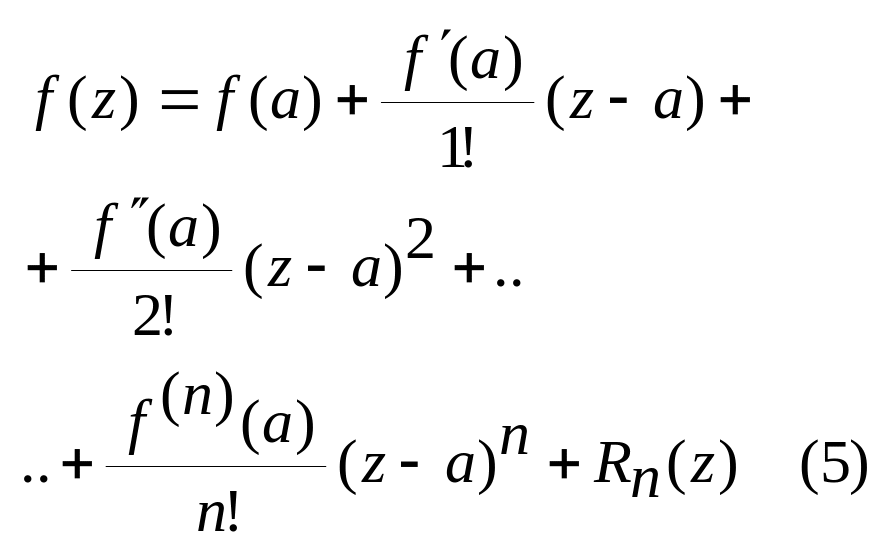
отримали ф-цію Тейлора. Ф-ла (5) наз ф-лую Тейлора. Якщо в ф-лі (5) то отримаємо ряд Тейлора. .

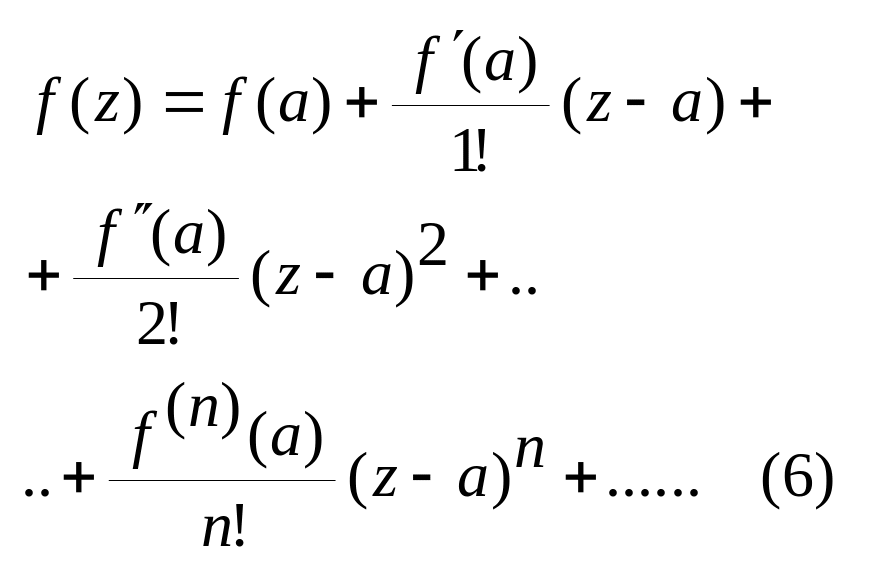
Теорема: ф-ція f(z) може бути записана у вигляді ряда Тейлора (6) в будь-якій відкритій обл , в якій вона аналітична. В будь-якій замкн області що належить цьому кругу ряд Тейлора збігається рівномірно.