8. Інтегральна теорема Коші для однозв’язної області.

Нех маємо однозв’язну обл

Теор1: Якщо - аналітична в однозв’язн обл , то інтеграл по б-якій кривій обл, що має спільн початок і спільн кінець набув одне й теж саме значення.

Дов:

u(x,y)=Ref(z), v(x,y)=Imf(z)

За умовами f(z) аналітична в обл. Д, тому викон. умова Коши Рімана:

а це є умова незалежності інтегралів.

В цьому випадку можна записати таким чином:

Теорема 2: Якщо f(z) аналітична в однозв’язній обл. Д , то 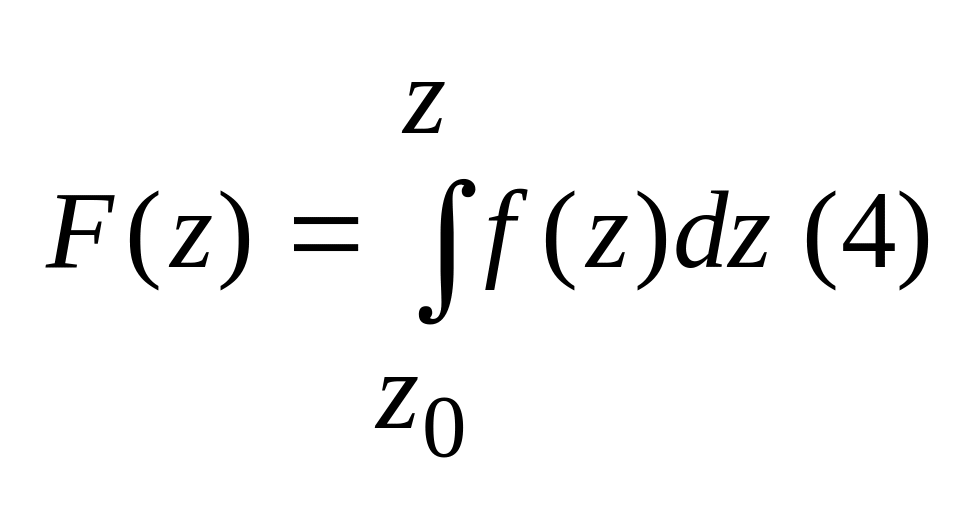, то F(z), де буде аналітичною в обл. Д, причому

Дов.

Виберемо довільну т z із Д і придамо цій точці приріст h такий, що (z+h) принадл. Д. Розглянемо .

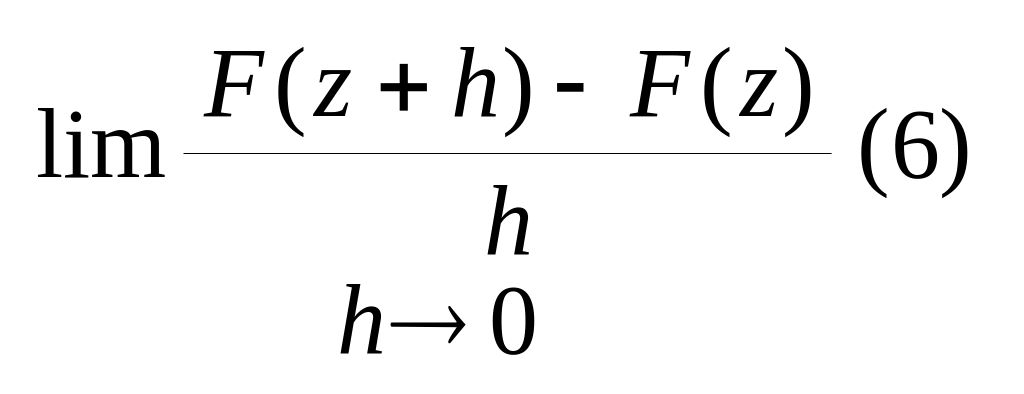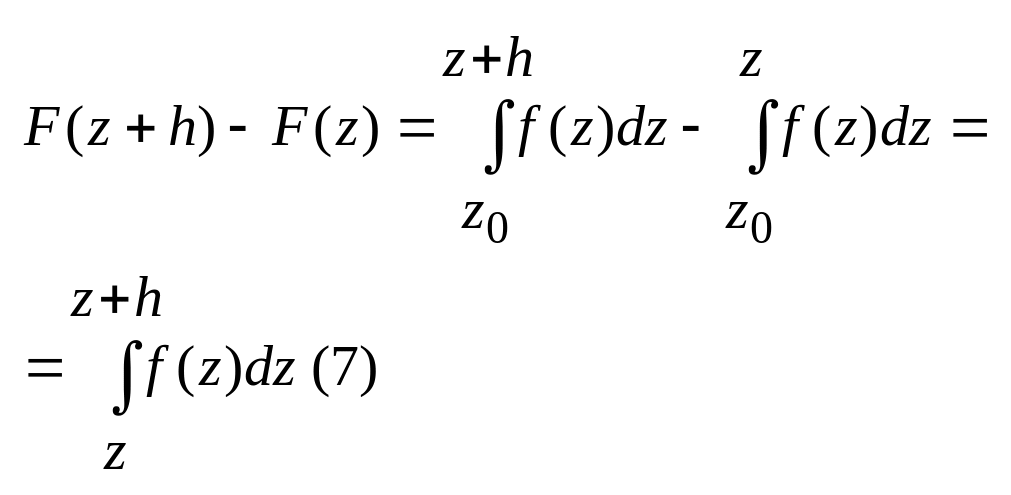
За умовами f(z) аналітична в обл. Д, тобто неперервна в цій обл. і має похідну.

Тоді де

Як тільки .

Підставимо (9) в (6):

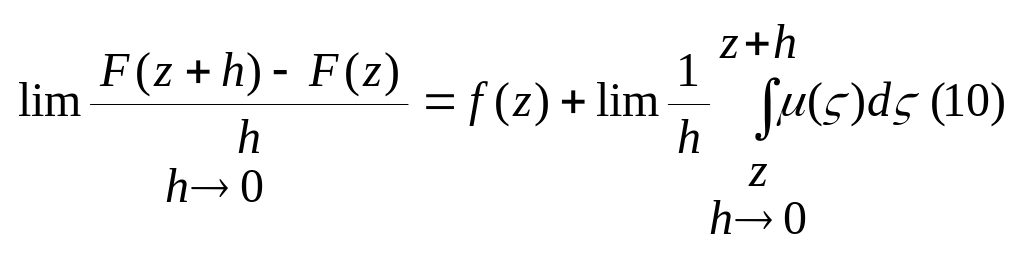Розглянемо інтеграл справа в (10)

Як відомо - велечина обмежена, а , а .

Звідси випливає, що 2-й доданок справа в (10) =0, тобто існує скінчена границя (6), вона дорівнює f(z), тобто викон. рів-ть (5).

Зауваження: F(z) для якої в обл. Д викон. рів-ть (5) наз. первісною функцією f(z).

Теорема 3:

Якщо f(z) має 2 первісні F₁(z) та F₂(z), то вони відрізняються не більш ніж за const (комплексну).

Дов:

Розглянемо

Причому:

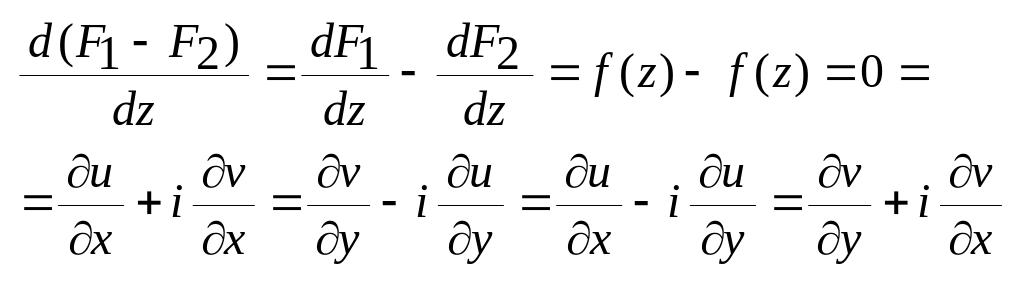
F₁-F₂=C₁+iC₂=C

Теорема 4 (інт. теорема Коши)

Якщо f(z) – аналітична а Д, то інтеграл від неї по будь-якому L, що належить Д = 0, тобто .

Дов.

Виберемо на L 2 різні точки. За теоремою

Тому

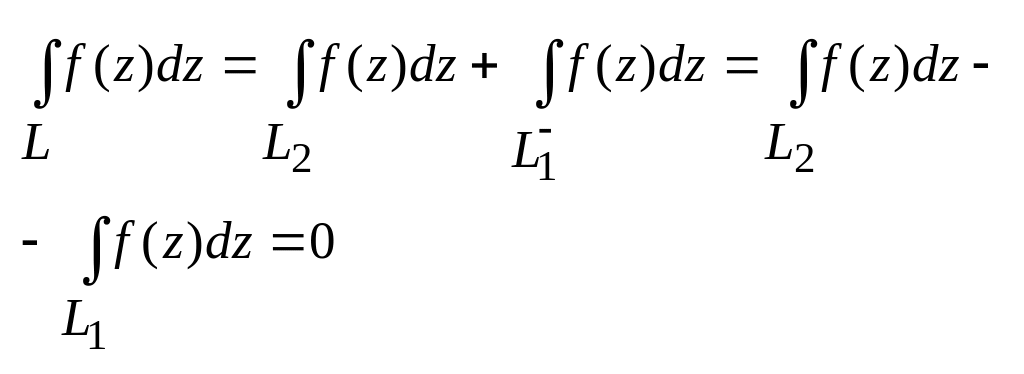
Теорема 5 (узагальнена інтег. теор. Коши)

Якщо f(z) аналітична в однозв. Д з межею Г і неперервна в обл. Д, то

9. Розповсюдження інтегральній теореми Коши на випадок багатозв’язній області.

Теорема: (інтегр. Т. Коши для багат. обл.)

Якщо f(z) аналітична в багатозв. обл. Д, то , де L₁ і L₂ прина-т Д. І мають однакові початок і кінець, набувають однакові значень, якщо крива L₁ може бути неперервнот трансформовано в криву L₂ не виходячи за межи обл. Д. Іншими словами, якщо лінії L₁ і L₂ обмежують обл., яка цілком складається з точок обл. Д.

Дов. Випливає з відповідної теореми для однозв. Обл..

Теорема (узагальнена інтег. теор. Коши для багат. обл.)

Якщо f(z) аналітична багатозв. обл. Д з межею Г і неперервна в замкненій Д, то при умові, що межу Г обходимо таким чином, що обл. Д залишається з одного боку.

Дов:

Зауважимо, що це теорема узагальнює теорему відповідну для однозв. обл.

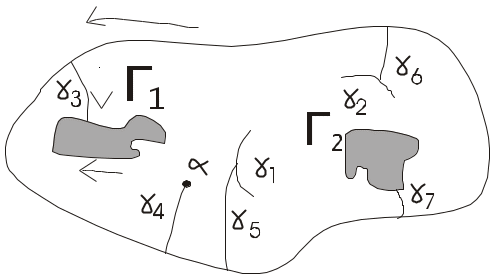
Зробимо такий розріз:

- обмежує однозв. обл.

f(z) буде аналітичною в обл. і неперервною в замкн. обл. Тоді за теоремою: , тобто

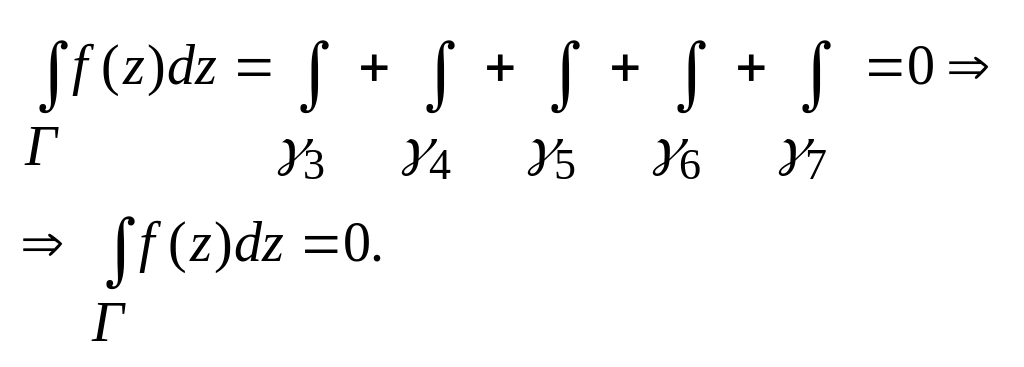
10. Інтегральна формула Коші

Т: Якщо функція аналітична в D і неперервна в , то для виконується (1), де L – межа (в дод. напрямку) обл.D.

Область D може бути будь-яка, але розглянемо однозв’язну область. Побудуємо окр. з центром в т.z, і радіусом r, r – настільки мале, що область обмежена складаєцця з .

Розглянемо область D₁, яка складаєцця з і не належить області, обмеженої . В цій обл. буде аналітичною.

Тоді згідно з узагальненою т.Коші для багатозв’яної обл.:

(2)

або (3)

тоді

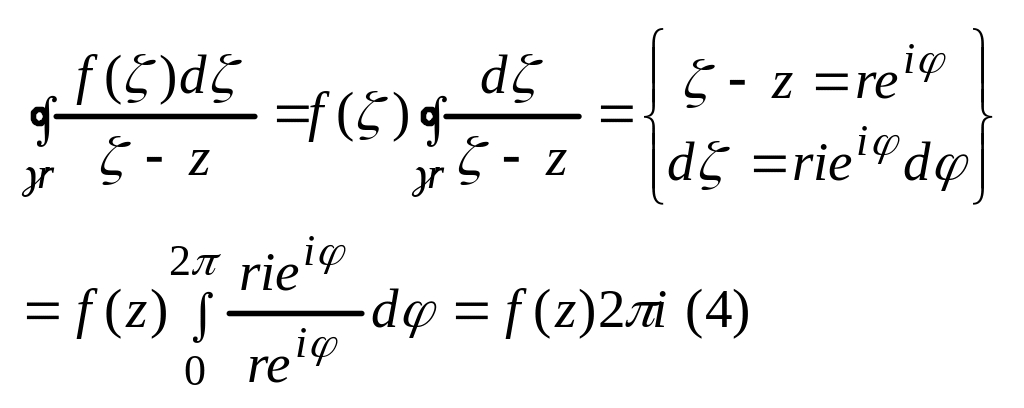
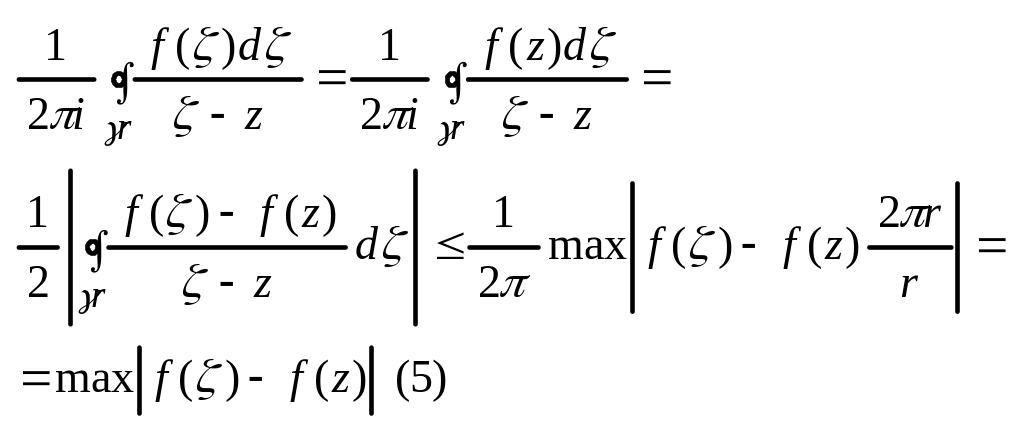За умовами ф-ція аналітична в області D, тобто неперервна. Тому, коли , то , та . Тобто після переходу (3) до праву частину можа замінити на праву частину (4). Отримаємо (1).