
- •1. Предмет и значение физики. Формы движения, изучаемые физикой. Механическое движение. Механика, ее составные части. Пространство и время в классической механике.
- •3. Линейные кинематические характеристики движения материальной точки
- •4. Основная задача кинематики
- •5. Свободное тело. Инерциальные системы. Первый закон Ньютона и его физическое содержание.
- •6. Сила. Масса. Импульс. Второй закон Ньютона и его физическое содержание. Принцип независимости взаимодействий. Третий закон Ньютона.
- •7. Замкнутая система. Закон сохранения импульса и его практическое применение. Замкнутая система – механическая система тел, на которую не действуют внешние силы.
- •9. Гравитационная сила. Закон всемирного тяготения. Гравитационное поле. Сила тяжести.
- •10. Вес тела. Реакция опоры. Сила упругости. Закон Гука. Силы трения.
- •11. Неинерциальные системы отсчета. Силы инерции.
- •12. Понятие энергии. Механическая энергия. Работа. Консервативные и неконсервативные силы.
- •14. Потенциальная энергия. Связь потенциальной энергии с силой. Графическое представление потенциальной энергии.
- •15. Закон изменения и сохранения механической энергии. Консервативные и диссипативные системы.
- •16. Применении законов сохранения энергии и импульса к абсолютно упругому и абсолютно неупругому ударам.
- •17. Твердое тело как система частиц. Понятие абсолютно твердого тела. Поступательное и вращательное движения абсолютно твердого тела. Центр инерции (масс) и его движение.
- •18. Основные кинематические характеристики вращательного движения и их связь с линейными кинематическими характеристиками.
- •19. Момент силы. Момент инерции. Теорема Штейнера. Момент импульса. Основной закон динамики вращательного движения.
- •20. Закон сохранения импульса системы тел. Работа сил при вращательном движении.
- •21. Кинетическая энергия тела, вращающегося на неподвижной оси. Полная кинетическая энергия твердого тела.
- •22. Преобразование координат Галилея. Правило сложения скоростей в классической механике. Механический принцип относительности.
- •2.1 Электрические заряды. Элементарный электрический заряд. Закон сохранения заряда.
- •2.2 Закон Кулона. Взаимодействие зарядов. Диэлектрическая проницаемость среды.
- •2.3 Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей.
- •2.4 Напряженность поля точечного заряда. Электрическое поле диполя. Графическое представление электрических полей.
- •2.6 Работа сил электростатического поля. Циркуляция вектора напряженности электрического поля.
- •2.7 Потенциал электростатического поля. Разность потенциалов. Эквипотенциальные поверхности.
- •2.8 Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.
- •2.10 Диэлектрики. Полярные и неполярные молекулы. Дипольные моменты молекул диэлектриков.
- •2.11 Поляризация диэлектриков. Свободные и связанные заряды.
- •2.12 Вектор поляризации. Диэлектрическая восприимчивость вещества.
- •2.13 Напряженность поля в диэлектриках. Вектор электрической индукции. Теорема Гаусса для поля в диэлектрике.
- •2.14 Классификация диэлектриков.
- •1.17 Связь между зарядом и потенциалом уединенного проводника. Электроемкость проводников. Конденсаторы.
- •2.18 Последовательное и параллельное соединение конденсаторов.
- •2.19 Энергия системы неподвижных точечных зарядов. Энергия заряженного проводника и конденсатора. Энергия электрического поля. Объемная плотность энергии.
- •3.3. Закон ома для однородного участка цепи в интегральной и дифференциальной форме.
- •3.4.Сопротивление. Зависимость сопрот металлов от температуры. Сверхпроводимость. Последоват и паралельн соединение.
- •3.6. Работа и мощность электротока. З-н джоуля-ленца.
- •4.1 Магнитное поле. Индукция магнитного поля. Силовые линии магнитного поля и их свойства.
- •4.2 Закон Био-Савара-Лапласа.
- •4.3 Применение закона Био-Савара-Лапласа к расчету магнитных полей: проводника конечной длины с током, кругового контура с током.
- •4.4 Циркуляция вектора индукции магнитного поля стационарных токов.
- •4.5 Применение теоремы о циркуляции вектора…
- •4.6 Действие магнитного поля на проводник с током. Сила Ампера.
- •4.7 Контур с током в магнитном поле. Магнитный момент контура с током.
- •4.8 Поток вектора индукции магнитного поля. Теорема Гаусса для магнитного поля.
- •4.9 Работа магнитного поля по перемещению проводника с контуров и контура с током.
- •4.11 Эффект Холла.
- •4.12 Магнитогидродинамический эффект. Мгд – генераторы.
- •4.13 Масспектрометры. Укорители заряженных частиц.
- •4.14 Магнетики. Намагничивание вещества. Гипотеза Ампера.
- •4.15 Намагниченность.
- •4.16 Напряженность магнитного опля.
- •4.17 Диамагнетики.
- •4.18 Парамагнетики.
- •4.19 Ферромагнетики.
- •4.20 Явление электромагнитной индукции. Закон Фарадея-Ленца и правило.
- •4.21 Явление электромагнитной индукции, как следствие закона сохранения энергии.
- •4.23 Токи Фуко.
- •4.25 Индуктивноссть. Явление самоиндукции.
- •4.26 Энергия магнитного поля.
- •5.12 Анализ изопроцессов в идеальном газе с использованием пнт.
- •5.18 Применение внт к анализу работы тепловых машин. Цикл Карно идеальной Тепловой машины. Кпд теплов машины. Обращённый цикл Карно.
- •5.19. Уравнение состояния реального газа. Теоретические и экспериментальные изотермы реального газа. Критическое состояние. Эффект Джоуля-Томпсона.
- •5.19 Уравнение состояния реального газа
5.18 Применение внт к анализу работы тепловых машин. Цикл Карно идеальной Тепловой машины. Кпд теплов машины. Обращённый цикл Карно.
Цикл Карно. В 1824 г. французский физик и инженер Н. Карно (1796-1832) опубликовал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно, в котором в качестве рабочего тела используют идеальный газ, заключенный в сосуд с подвижным поршнем. Цикл Карно, где изотермическое расширение и сжатие заданы соответственно кривыми 1-2 и 3-4, адиабатическое расширение и сжатие - кривыми 2-3 и 4-1.Он самый экономичный и представляет собой круговой процесс, состоящий из двух изотерм и двух адиабат. Согласно (Коэффициент полезного действия для кругового процесса =А/Q=( Q1-Q2)/ Q1= 1- Q2/Q1) КПД цикла Карно =А/Q=( Q1-Q2)/ Q1= 1- Q2/Q1, где Q1- количество теплоты, полученное газом от нагревателя, температура которого Т1, Q2- количетво теплоты, отданное газом холодильнику, температура которого Т2. Карно показал, что для такого цикла =(Q1-Q2)/Q1=(Т1-Т2)/Т1=1-Т2/Т1, т.е. КПД определяется только температурами нагревателя и холодильника. Т2/T1=Q2/Q1. Карно предположил, что этот результат справедлив для любых термодинамических систем. Обратный цикл Карно положен в основу действия тепловых насосов. Тепловые насосы должны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Большая часть этой энергии отбирается от окружающей среды с низкой температурой и меньшая часть - получается за счет механической работы, производимой, например компрессором.
5.19. Уравнение состояния реального газа. Теоретические и экспериментальные изотермы реального газа. Критическое состояние. Эффект Джоуля-Томпсона.
 Действие сил
притяжения между молекулами реального
газа приводит к появлению дополнительного
давления на газ, наз внутренним давлением.
По вычислениям Ван-дер-Ваальса, внутр
давление p’=a/V2m
где а пост Ван-дер-Ваальса, хар-я силы
межмолекулярного притяжения, Vm-молярный
объём. Получаем Ур-е состоян реальных
газов. (p+
a/V2m)(Vm-b)=RT,
для произволной массы: (p+v2
a/V2)(V-vb)=vRT.
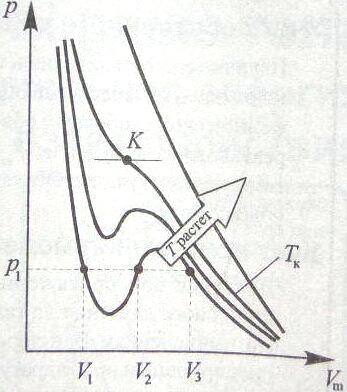
Расс изотермы
Ван-дер-ваальса – кр зависимости p
от Vm
при заданных Т. Преобраз Ур-е к виду:
pV3-(RT+pb)V2+aV-fb=0.
На участках при Т<Tk
на участках 1-3 5-7 при ↓V
- ↑p,
что естественно, но 3-5 – сжатие вещ-ва
приводит к уменьшению давления, реально
это невозможно. Наличие 3-5 значит, при
постеп изменен V
вещ-во не может оставаться всё время в
виде однород среды; - скачки состояния,
рапад вещ-ва на 2 фазы. Реальная изотерма
будет 7-6-2-1. (7-6 газ, 2-1- жидкое). Реальные
и теоритич изотермы отлич тем, что
превращению газа в жидкость в 1м случае
соответств горизонтал участки, во 2м –
волнообразные. С ростом температуры
область горбов и впадин на изотерме ВдВ
уменьшается и при температуре ТКР
- критической температуре - превращается
в точку перегиба К
с горизонтальной
касательной. В точке К
исчезают различия между жидкой и
газообразной фазой (однородная среда).
Она имеет 1 точку перегиба К, наз
критической
точкой; в
этой точке касат к ней параллельн ОХ,
соответсв её V&p
– критические.
PkV3-(RTk+pkb)V2+aV-ab=0,
pk(V-Vk)3=0
или pkV3-3pkVkV2+3pkV2kV-pkV3k=0,
тогда: pkV3k=ab,
3pkVk=a;
3pkVk=RTk+pkb,
решаем: Vk=3b,
pk=a/27b2,
Tk=8a/27Rb.
Проведём линию через К, (см рис.) Эта
кривая и критич изотерма делят диаграмму
под изотермой на 3области: жидкость+газ,
жидкое, газ. Пар может быть при изотерм
сжатии превращ в жидкость, газ так
неможет. Послед соотнош довольно
приближенны. Внутренняя энергия моля
реального газа U=CVТ
-a/V, т.е.
меньше энергии идеального газа U=CVТ.
Для произвольной массы реального газа
U=(CVТ
-a/V)
Действие сил
притяжения между молекулами реального
газа приводит к появлению дополнительного
давления на газ, наз внутренним давлением.
По вычислениям Ван-дер-Ваальса, внутр
давление p’=a/V2m
где а пост Ван-дер-Ваальса, хар-я силы
межмолекулярного притяжения, Vm-молярный
объём. Получаем Ур-е состоян реальных
газов. (p+
a/V2m)(Vm-b)=RT,
для произволной массы: (p+v2
a/V2)(V-vb)=vRT.
Расс изотермы
Ван-дер-ваальса – кр зависимости p
от Vm
при заданных Т. Преобраз Ур-е к виду:
pV3-(RT+pb)V2+aV-fb=0.
На участках при Т<Tk
на участках 1-3 5-7 при ↓V
- ↑p,
что естественно, но 3-5 – сжатие вещ-ва
приводит к уменьшению давления, реально
это невозможно. Наличие 3-5 значит, при
постеп изменен V
вещ-во не может оставаться всё время в
виде однород среды; - скачки состояния,
рапад вещ-ва на 2 фазы. Реальная изотерма
будет 7-6-2-1. (7-6 газ, 2-1- жидкое). Реальные
и теоритич изотермы отлич тем, что
превращению газа в жидкость в 1м случае
соответств горизонтал участки, во 2м –
волнообразные. С ростом температуры
область горбов и впадин на изотерме ВдВ
уменьшается и при температуре ТКР
- критической температуре - превращается
в точку перегиба К
с горизонтальной
касательной. В точке К
исчезают различия между жидкой и
газообразной фазой (однородная среда).
Она имеет 1 точку перегиба К, наз
критической
точкой; в
этой точке касат к ней параллельн ОХ,
соответсв её V&p
– критические.
PkV3-(RTk+pkb)V2+aV-ab=0,
pk(V-Vk)3=0
или pkV3-3pkVkV2+3pkV2kV-pkV3k=0,
тогда: pkV3k=ab,
3pkVk=a;
3pkVk=RTk+pkb,
решаем: Vk=3b,
pk=a/27b2,
Tk=8a/27Rb.
Проведём линию через К, (см рис.) Эта
кривая и критич изотерма делят диаграмму
под изотермой на 3области: жидкость+газ,
жидкое, газ. Пар может быть при изотерм
сжатии превращ в жидкость, газ так
неможет. Послед соотнош довольно
приближенны. Внутренняя энергия моля
реального газа U=CVТ
-a/V, т.е.
меньше энергии идеального газа U=CVТ.
Для произвольной массы реального газа
U=(CVТ
-a/V)
Э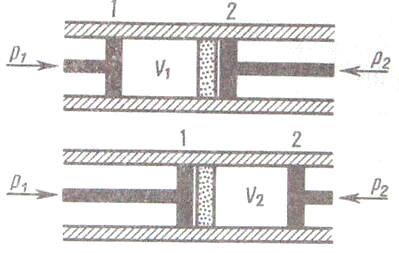 ффект
Джоуля-Томпсона (ДТ)
в теплоизолир трубке с порстой перегородкой
находятся два поршня, которые могут
перемещ без трения. Пусть сначала слева
от перегородки газ нах под P1
, занимает V1
и облад-т T1.
а справа нет газа. После прохождения
газа через перегородку в правой части
газ имеет p2,
V2,
T2,
ффект
Джоуля-Томпсона (ДТ)
в теплоизолир трубке с порстой перегородкой
находятся два поршня, которые могут
перемещ без трения. Пусть сначала слева
от перегородки газ нах под P1
, занимает V1
и облад-т T1.
а справа нет газа. После прохождения
газа через перегородку в правой части
газ имеет p2,
V2,
T2,
давления P1 и P2 постоянны. Т.к. расширение газа происх без теплообмена с окр средой, то на основ ПНТ: dQ=(U2-U1)+dA=0 внешняя работа >0 при полож поршня 2 и А<0 в полож 1, т.е dA=A2-A1, U1+p1V1=U2+p2V2(2), т.о. U+pV=const и наэ энтальпией. Расчёт для моля газа: подставив в (2) выражение pkV3-3pkVkV2+3pkV2kV-pkV3k=0 и рассчитанные из ур-я (2) значения p1V1 и p2V2 получим:
п![]()
![]() отом
следует что знак разности ∆Т зависит
от того, какая из поправок ВдВ играет
большую роль. Сделав допущение p2<<P1
и V2>>V1
отом
следует что знак разности ∆Т зависит
от того, какая из поправок ВдВ играет
большую роль. Сделав допущение p2<<P1
и V2>>V1
1)a≈0 .
2) b≈0
Т .е
знак разности температур зависит от
значений начального объёма и нач Т.
Изменен Т реал газа в результате его
адиабатич дросселирования – медленного
прохождения газа под действием перепада
давления сквозь дроссель наз эффектом
Джоуля-Томсона. Его принето называть
положительным, если газ в проц охлаждается,
и отриц, если нагрев. В зависимости от
дросселир один газ может быть + и –
эффект ДТ.
.е
знак разности температур зависит от
значений начального объёма и нач Т.
Изменен Т реал газа в результате его
адиабатич дросселирования – медленного
прохождения газа под действием перепада
давления сквозь дроссель наз эффектом
Джоуля-Томсона. Его принето называть
положительным, если газ в проц охлаждается,
и отриц, если нагрев. В зависимости от
дросселир один газ может быть + и –
эффект ДТ.
