5.12 Анализ изопроцессов в идеальном газе с использованием пнт.

И зохорический процесс, (з-н Шарля). Для него V=const. Процесс 1-2 соответствует нагреванию, а процесс 2-1 - охлаждению газа. При изохорическом процессе газ не совершает работы: =0 и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии, т.е. Q=dU. (11) Согласно формуле (3) для произвольной массы газа и поэтому , (12) и молярная теплоемкость при постоянном объеме

. (13) Таким образом, . (14)

Изобарический процесс(Гей Люссака). Для него P=const.. Практически он осуществляется, например, при нагревании (1-2) или охлаждении (2-1) газа, находящегося в цилиндре с подвижным поршнем, на который действует постоянное внешнее давление.

У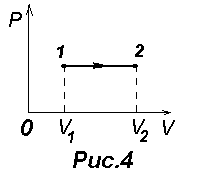 читывая, что для произвольной массы газа U=(i/2)RT, PV=RT, запишем ПНТ в дифференциальной форме для изобарического процесса: , (15)Молярная теплоемкость при постоянном давлении . (16) Выражение (17)называется уравнением Майера; оно показывает, что C_P всегда больше C_V на величину универсальной газовой постоянной R. Это объясняется тем, что для нагревания газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа. Таким образом, физический смысл универсальной газовой постоянной R: она численно равна работе, совершаемой одним молем идеального газа при его изобарическом нагревании на 1 К.С учетом (16) первое начало термодинамики для изобарического процесса имеет вид , (18) кроме того, , .

Изотермический процесс. Для него Т-const. Например, процессы кипения, конденсации, плавления и кристаллизации химически чистых веществ происходят при постоянной температуре, если внешнее давление постоянно. Для идеального газа при Т=const выполняется закон Бойля-Мариотта PV=const. Процесс 1-2 соответствует нагреванию газа, а процесс 2-1 - охлаждению его. Внутренняя энергия идеального газа в изотермическом процессе не изменяется, т.е. =0, так как Т=const и dT=0. Таким образом из ПНТ ( ) следует, что , т.е. вся теплота, сообщаемая газу, расходуется на совершение им работы против внешних сил:

, (19) где=m/M - число молей. Процесс 1-2 соответствует изотермическому расширению газа, в этом случае Q₁₂>0 и A₁₂>0. Обратный процесс 2-1 соответствует изотермическому сжатию газа, для него Q₁₂<0 и A₁₂<0.

5.13. Адиабатическая замкнутая система. Уравнение Пуассона. Адиабатический процесс. Это процесс, при котором отсутствует теплообмен ( ) между системой и окружающей средой. К адиабатическим можно отнести все быстропротекающие процессы. Из ПНТ ( ) для адиабатического процесса следует, что ,(20)т.е. внешняя работа совершается за счет уменьшения внутренней энергии системы. Учитывая, что , найдем работу адиабатического расширения газа от объема V₁ до V₂ ( при этом температура газа уменьшается от Т₁ до Т₂):

. (21) Можно показать, что для адиабатического процесса(он противоположен изотермич) . (22)

Э то уравнение называют уравнением Пуассона или уравнением адиабаты, =С_P/C_V=(i+2)/i - показатель адиабаты (коэффициент Пуассона), i - число степеней свободы молекулы газа. Для перехода к переменным T,Vили збЕ исключим из Ур-я с помощью Менд-Клапер P или V: TV^γ-1=const, T^γp^1-γ=const. Это Ур-я адиабатич процесса. Величина безразмерная На диаграмме PV линия, изображающая адиабатический процесс, называется адиабатой (рис.6.). Так как >1, то адиабата идет круче, чем изотерма, уравнение которой PV=const. Процесс 1-2 соответствует адиабатическому расширению газа. В этом случае , dU>0. Обратный процесс 2-1 соответствует адиабатическому сжатию газа. В этом случае , dU<0.

5 .14 Обратимые и необратимые процессы. Термодинамическая вероятность. ТД процесс назыв обратимым, если он может происходить как в прямом так и обратном направлениях, причём если такой процесс происх сначала в прямом , а затем в обратном и сис возвращ в исходное состояние, то в окруж среде и в этой сис не происходит никаких изменений. Процесс неудовлетвор этим условиям явл необратимым(не допускают возвращение сис в исх полож без изм в окр среде.. Любой равновесный процесс явл обратимым. Обратимые проц-ы это в какой-то степени идеализация реал проц-в. Равновесные – в ходе котор все параметры ТДС меняются совершенно одинак в любой части этой системы. Т.к. реальные проц-ы прох с конечн скоростью, то они все необратимые. Для необратимых проц хар особенность: они протекают тока в 1м направлении.(Н-р: растворение сахара в воде). ТД вероятность- величина микростадий через которые может быть реализ. данные микросостояния. w=N!/N₁!N₂!N_n!, где N – всего молекул, N_n – молек в ячейке.

1)Все молекулы в 1й яйч/ - w=1 2) 1 молек нах внизу, 3 сверху, w=4; 3) w=6.

5 .15. Энтропия, её статистическое определение. Измерение энтропии при обратимом изопроцессе. Приведённая теплота процесса. Феноменологическое определение энтропии. Энт явл мерой неупорядоченности сис. энтропия связывается с термодинамической вероятностью состояния системы. Энтропия – СФВ хар-я состояние ТД сис и которая явл мерой вероятности осуществления данного макросостояния сис и числ S=klnW. Термодинамическая вероятность W состояния системы - это число способов, которыми может быть реализовано данное состояние макроскопической системы или число микросостояний, осуществляющих данное макросостояние. По определению W1 , т.е. термодинамическая вероятность не есть верояность Р в математическом смысле (Р1).(Н-рмакросостояние моля кислорода, соответствующее Р=1 физической атмосфере и Т=300К, может быть осуществлено числом микросостояний W= )Больцман в 1872 г. показал, что энтропия системы и ТД вероятность связаны между собой формулой S=klnW, Утверждение 2го начала ТД о невозможности убывания энтропии в изолир сис может быть истолковано статистически, на лснове МКТ строения вещ-в этой формулой, где k - постоянная Больцмана. Свойства энтропии:1)величина аддитивная 2)если сис сост из подсис, то S суммир-ся 3)S связ с энегетич хар-ми 4)она сама мера себе. Физ смысл имеет не сама, а разность энтропий.

∆S =kLnw₂-kLnw₁=kLn(w₂/w₁) → w₂/w₁=(V₂/V₁)^N ; ∆S=kNLn(V₂/V₁)=kN_AvLn(V₂/V₁)=kNA*(m/M)*Ln(V₂/V₁)=R*m/M*Ln(V₂/V₁)=∆S. ∆S=Q/T →

Э нтропия – СФВ хар состояние ТДС приращ котор при обратим процессе = кол-ву приведённого тепла, полученного в этом процессе.

П риведённая теплота – отношение теплоты Q, получ телом в изотермич процессе к температ Т теплоотдающего тела. Привед кол-во теплоты, сообщ телу на бесконечн малом участке

5 .16. расчёт энтропии для обратимых и необратимых процессов. Второе начало ТД. Выражая всеобщий закон сохранения и превращения энергии, ПНТ не позволяет определить направление протекания процессов. Действительно, процесс самопроизвольной передачи теплоты от холодного тела к горячему не противоречит ПНТ, если только уменьшение внутренней энергии холодного тела равно энергии, полученной горячим телом. Однако, опыты показывают, что такой процесс не происходит (раскаленный кусок железа, опущенный в воду, не нагревается за счет охлаждения воды).Обобщение огромного экспериментального материала привело к необходимости формулирования второго, третьего и нулевого начал термодинамики.ВНТ в отличие от ПНТ не является всеобщим законом природы. Оно справедливо только по отношению к термодинамическим системам. Существует несколько эквивалентных формулировок ВНТ.1. Невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему (формулировка Клаузиуса, 1850 г.).2. Невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела (формулировка Томсона, 1851 г., в 1892 г Томсон получил титул лорда Кельвина).Соответственно этой формулировке была доказана невозможность вечного двигателя второго рода, который целиком превращал бы в работу теплоту, извлекаемую из окружающих тел (океана, атмосферного воздуха и др.) Согласно формуле (24) для него было бы Q₂=0, A=Q₁, =1. Таким образом, это невозможно. Заметим, что ПНТ не противоречило бы создание такого двигателя.3. Энтропия изолированной системы не может убывать при любых происходящих в ней процессах, т.е. dS0, где знак равенства относится к обратимым процессам, а знак больше - к необратимым процессам.(Формулировка Клаузиуса, 1865 г.)

В 1876 г. Клаузиус дал наиболее общую формулировку ВНТ: при реальных (необратимых) адиабатических процессах dS>0, т.е. энтропия возрастает, достигая максимального значения в состоянии равновесия. Формула Больцмана (31) S=klnW позволяет дать статистическое истолкование третьей формулировки ВНТ: Термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать.Итак, ВНТ является статистическим законом.Оно выражает необходимые закономерности хаотического движения большого числа частиц, входящих в состав изолированной системы. Формулировка Кельвина-Планка: 1)вечн двиг 2го рода невозможен; 2)невозможен процесс, единственным результатом которого явл превращение теплоты, получ от нагревателя, в эквивалентную ей работу. Содерж ВНТ: теплота никогда не может переходить сама собой от тел с более низкой Т к телам с более высокой Т.

РАСЧЁТ S ПРИ НЕОБРАТИМОМ ПРОЦ-Е.

Убираем шарики из чашки – лесенкой уменьшается P, A_обрат>A_{необрат}; Q_обрат=A_обрат+∆U_обр; Q_{необрат}=А_необр+∆U_необр ; Q_необ<Q_обр «если необатимый=если обратимый»

5 .17. статистический смысл 2го начала ТД (ВНТ). Границы его применимости. Возрастание энтропии означает переход сис из менее вероятных в более вероятные состояния. Термо изолир сис – наз сис котор необменив таплом с окр средой её телами – адиабатич изолир сис.∆S=Q/T=0 ∆S>=0 Энтропия изолированной системы не может убывать при любых происходящих в ней процессах, т.е. dS0, где знак равенства относится к обратимым процессам, а знак больше - к необратимым процессам.(Формулировка Клаузиуса, 1865 г.) В 1876 г. Клаузиус дал наиболее общую формулировку ВНТ: при реальных (необратимых) адиабатических процессах dS>0, т.е. энтропия возрастает, достигая максимального значения в состоянии равновесия. Формула Больцмана S=klnW позволяет дать статистическое истолкование формулировки ВНТ: Термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать. Итак, ВНТ является статистическим законом.

Пределы применимости второго начала

Пределы применимости начал термодинамики определяются рамками самой термодинамики, её исходными положениями. Законы термодинамики неприменимы к микросистемам, размеры которых сравнимы с размерами молекул. Верхняя граница применимости второго начала связана с ограничением применения термодинамики к системам галактических размеров. Применение второго начала ко всей Вселенной приводит к "тепловой смерти Вселенной". В противовес концепции "тепловой смерти" Л.Больцман выдвинул флуктуационную гипотезу. Установив статиcтическую природу второго начала, Больцман показал, что равновесное состояние является лишь наиболее часто встречающимся состоянием. По Больцману вся Вселенная находится в равновесии, а наша часть является флуктуационным отклонением.