4.25 Индуктивноссть. Явление самоиндукции.

Явление самоиндукции заключается в появлении ЭДС индукции в самом проводнике при изменении тока в нём. Примером явления самоиндукции является опыт с двумя лампочками, подключенными параллельно через ключ к источнику тока, одна из которых подключается через катушку (рис.4). При замыкании ключа лампочка 2, включённая через катушку, загорается позже лампочки 1. Это происходит потому, что после замыкания ключа ток достигает максимального значения не сразу, магнитное поле нарастающего тока породит в катушке индукционную ЭДС, которая в соответствии правилом Ленца будет мешать нарастанию тока. Для самоиндукции выполняется установленный опытным путём закон: ЭДС самоиндукции прямопропорциональна скорости изменения тока в проводнике.?=LI/t

Коэффициент пропорциональности L называют индуктивностью. Индуктивность - это величина, равная ЭДС самоиндукции при скорости изменения тока в проводнике 1 A/c. Еденица индуктивности - генри (Гн). 1Гн=1В*с/A. 1 генри- это индуктивность такого проводника, в котором возникает ЭДС самоиндукции 1 вольт при скорости изменения тока 1 A/c. Индуктивность характеризует магнитные свойства электрической цепи (проводника), зависит от магнитной проницаемости среды сердечника, размеров и формы катушки и числа витков в ней.

При отключении катушки индуктивности от источника тока лампа, включённая параллельно катушке, даёт кратковременную вспышку (рис.5). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия магнитного поля находится по формуле W=LI?/2.

Энергия магнитного поля зависит от индуктивности проводника и силы тока в нём. Эта энергия может переходить в энергию электрического поля. Вихревое электрическое поле порождается переменным магнитным полем, а переменное электрическое поле порождает переменное магнитное поле, т.е. переменные электрическое и магнитное поля не могут существовать друг без друга. Их взаимосвязь позволяет сделать вывод о существовании единого электромагнитного поля. Электромагнитное поле - одно из основных физических полей, посредством которого осуществляется взаимодействие электрически заряженных частиц или частиц, обладающих магнитным моментом. Электромагнитное поле характеризуется напряжённостью электрического поля магнитной индукцией. Связь между этими велечинами и распределением в пространстве электрических зарядов и токов была установлена в 60- годах прошлого столетия Дж. Максвеллом. Это связь носит название основных уравнений электродинамики, которые описывают электромагнитные явления в различных средах и в вакууме. Получены эти уравнения как обобщение установленных на опыте законов электрических и магнитный явлений.

4.26 Энергия магнитного поля.

Наличие индуктивности у соленоида приводит к тому, что при изменении силы протекающего через него тока в катушке возникает ЭДС, стремящаяся противодействовать этому изменению. В результате наличие в электрических цепях элементов с большой индуктивностью делает в них невозможными скачкообразные изменения силы тока. Простой расчет (12.31) показывает, что в цепи, содержащей сопротивление и катушку, по которой в начальный момент протекал заданный ток, сила тока будет убывать во времени по экспоненциальному закону.

При этом на сопротивлении, согласно закону Джоуля Ленца, будет выделяться тепло. Полная тепловая энергия (12.32), выделявшаяся на сопротивлении, очевидно, первоначально была где-то запасена. Логично считать, что эта энергия связана с магнитным полем, аналогично тому, как существует энергия, связанная с полем электрическим.

В таком случае энергия рассматриваемой системы первоначально находилась внутри соленоида, а ее объемная плотность определяется выражением (12.33), которое легко получить, используя формулы для магнитного поля внутри соленоида (12.28) и его индуктивности (12.30). Обращает на себя внимание аналогия между выражениями для объемных плотностей электрической и магнитной энергий. Полученная на частном примере формула для объемной плотности магнитной энергии оказывается верной и в общем случае.

5 .1. Статистический и термодинамический методы изучения макроскопических тел. Молекулярная физика и термодинамика изучают один и тот же круг явлений, а именно макроскопические процессы в телах. Физические свойства макроскопических систем, состоящих из большого числа частиц, изучаются двумя взаимно дополняющими методами: статистическим и термодинамическим. Статистический метод основан на использовании теории вероятностей и определенных моделей строения изучаемых систем. В совокупном поведении большого числа частиц, координаты и импульсы которых случайны в любой момент времени, проявляются особые статистические закономерности. Например, в газах можно определить средние значения скоростей молекул и их энергий, однозначно связанных с температурой. Раздел физики, в котором с помощью статистического метода изучаются физические свойства макроскопических систем, называется статистической физикой. Второй, термодинамический метод исследования поведения большого числа молекул При термодинамическом методе исследования не рассматривается внутреннее строение изучаемых тел, а анализируются условия и количественные соотношения при различных превращениях энергии, происходящих в системе. Раздел физики, в котором физические свойства макроскопических систем изучаются с помощью термодинамического метода, называется термодинамикой. Статистическая физика и термодинамика при малом числе частиц теряют смысл. Термодинамика имеет дело с термодинамической системой - совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой).

5.2 термодинамич параметры(p, T, V).Состояние системы задается термодинамическими параметрами (параметрами состояния). Обычно в качестве параметров состояния выбирают: - объем V, м³; давление Р, Па, T. P – СФВ хар-я распред силы по поверхн-ти, числ=отношению перпендик-ра составляющ-й силы к величине поверхности. (Р=dF_n /dS, где dF_n - модуль нормальной силы, действующей на малый участок поверхности тела площадью dS, ,1бар=10^5Па;1 Па=1 Н/м²; 1мм рт.ст=133,3Па;1технич атм=9,8*10⁴Па); термодинамическую температуру Т, К (Т=273.15+t).Т-СФВ хар интенсивн хаотич(теплового) движ молекул, Т=a<E_k>. Термодинамическая температура прежде именовалась абсолютной температурой. Понятие температуры, строго говоря, имеет смысл только для равновесных состояний. Равновестн состояние – такое состояние, при котором все параметры хар сис с течением времени не меняются. Термодинамическое определение Т – мера отклонения состоян термодинам сис от состоян той сис котор принета за состоян сис с Т=0. Молярный объём – физ величина, равная отношен V газа к числу N молей, содерж в газе: V_m=V/N, масса моля числ равна µ, V_µ=µv, где v-удельный объём.

5.3. Основн задачи и положения классич статики. Основы МКТ. Задачи: 1)как распределены частицы по координ скоростям, импульсам энергии. 2)как связ параметры ИГ (Р, V, Т) с хар-ками отдельных частиц. Основные положения МКТ. 1)молекулы макросис нах-ся в состоян хаотич непрерывн движения.2)каждую молекулу можно отличить от др.3)физ хар молекулы(скорость, импульс, энергия)меня.тся непрерывно.4)в одном и том же состоянии(иметь одинак физ хар молекулы может нах-ся любое кол-во молекул.5)Скорость частиц могут менятся от 0 до бесконеч-ти. ИГ: Идеальным называется газ, молекулы которого имеют пренебрежимо малый собственный объем и не взаимодействуют друг с другом на расстоянии.Оказывается при нормальных условиях, т.е. давлении Р₀=1.01310⁵Па (что эквивалентно 760 мм ртутного столба или одной физической атмосфере) и температуре Т₀=273.15 К (t=0 C) многие газы (Н₂, О₂, N₂, воздух и др.) можно считать с хорошим приближением идеальными. В самом деле, учитывая, что эффективные диаметры d молекул различных газов имеют величины порядка 10^-10 м и при нормальных условиях концентрация молекул n=N/V 10²⁵ м^-3, то среднее расстояние между молекулами <r> 10^-8 м, т.е. столь велики по сравнению с d=10^-10 м, что силами притяжения можно пренебречь. Суммарный собственный объем всех N 10²⁵ молекул, содержащихся в 1 м³, Nd³/6=10^-5 м³ << 1 м³. Cледовательно, собственным объемом молекул газа тоже можно пренебречь.Таким о бразом, многие газы можно считать с хорошим приближением идеальными.Опытным путем было установлено, что при обычных условиях параметры состояния газов подчиняются уравнению Клапейрона РV/T=B=const. (1)Оказалось также, что чем разреженнее газ, тем точнее выполняется это уравнение. Идеальный газ строго подчиняется уравнению (1), которое, следовательно, является уравнением состояния идеального газа.Согласно закону Авогадро, при нормальных условиях, т.е. при температуре t=0 C (Т₀=273.15 К) и давлении одна физическая атмосфера (Р₀=1.01310⁵Па) объем моля любого газа равен V₀=22.4 л/моль=22.410^-3 м³/моль.(Напомним, что единицей количества вещества в СИ является моль. Один моль любого газа содержит одно и то же число молекул N_A=6.0210 ²³ моль^-1, называемое постоянной Авогадро. Массу моля обозначают буквой М). Если m₀ - масса одной молекулы, то масса моля или молярная масса М=m₀N_A. (2)Например, для кислорода О₂ M=0.032 кг/моль, для азота N₂ M=0.028 кг/моль. Подставляя эти значения в (1) и обозначая константу В для одного моля буквой R, находим R= Р₀V₀/T₀=1.01310^522.410^-3/273.15=8.31 Дж/мольК.(3)Константу R называют универсальной газовой постоянной.Следовательно, уравнение состояния для моля идеального газа имеет видРV=RT.(4)Для произвольной массы m газа можно переписать уравнение (4) в видеРV=(m/M)RT или РV=RT, (5)где =m/M - число молей. Очевидно, что =N/N_A,(6)где N - число молекул, содержащихся в массе газа m.В такой наиболее общей форме записи уравнение состояния идеального газа (5) называется уравнением Клапейрона-Менделеева. Употребляется еще одна форма уравнения (5). Введем постоянную Больцмана k=R/N_A. (7)Тогда из уравнения (5) получим РV= (N/N_A )RT=NkT. (8)Разделив обе части этого уравнения на объем газа V получим Р= nkT, (9) где n=N/V - концентрация молекул, м^-3. Уравнения (1), (5), (8), (9) представляют собой различные формы записи уравнения состояния идеального газа. ИГ – простейшая модель реальных газов. 1)молекулы не имеют размера 2)на расстоянии молек не взаимод-т, кроме абсолютно упругих столкновен. 3)в промежутке между соударениями молекулы движутся равномерно и прямолинейно.

5.4. Распределение молекул ИГ по скоростям. Наиболее вероятная, среднеквадратическая и среднестатистическая скорости молекул. Опыт Штерна. <V>молек, наиболее вероятн V_в, среднеквадратич V_кв=(<V²>)^0,5, dn/n –доля частиц ИГ имеющих скорости от V до V+dV, f(V)-доля молекул взятых в близи некой V и приход на единич интервал скоростей. -…- вероятность обнаружения частицы в близи некоторого знач скорости в пределах единичного интервала скоростей. Конкретный вид f(V) был получен с использ вероятности в 1859г Максвеллом. dn/n-f(V)=[A₁e^(-mv²/2kT)]*V²,-з-н для распределения, гдеA₁=4п(m₀/2пkT)^1,5, k – постоянная Больцмана. , V₀=(2kT/m)^0,5; Опыт Штерна – опят, подтверждаемый экспериментально справедливость функц распределения молек по скоростям получ теорией Максвелла. Суть: установка его: вдоль оси внутр цилиндра со щелью натянута платиновая проволока, покрыт серебром, нагреваемая током при откач воздухе. При нагрев – серебро испар-ся. Атомы Ag вылетая через щель попадают на внут поверхн второго цилиндра, давая изображение цилиндра. Если прибор привести во вращение вокруг общей оси цилинд, то атомы осядут не на против щели, а сместятся на расстоян s. Изображение получ размытым. Исследую толщину осадочн слоя, можно оценить распределение молек по скоростям. Итак существуют три формулы для определения скорости молекул газа: (18), (31), (32). Согласно этим формулам v_B<v> v_СР.КВ=   =1 1,13  1,22.Таким образом, средняя и средняя квадратичная скорости превышают наиболее вероятную скорость на 13 и 22 % соответственно, т.е. отличие не очень большое.

5.5 Распределение молекул ИГ по энергиям. Статистическое толкование температуры. Постоянная Больцмана. Исходя из распределения молекул по скоростям, можно найти распределение молекул газа по кинетическим энергиям поступательного движения молекул W_к=mv²/2. Это распределение характеризуется функцией f(W_к), которая вводится аналогично f(v)

* N, хде N- число молекул. Распределение молек ИГ по энергиям определяют долю dN(E)/N из общего числа молекул, которые имеют E_k, заключ в интервале от E до E+dE. Пример: найдём E_k ИГ: Т=2/3*kE_k T=0 → <E_k>=0 прекращ тепловое движение частиц. /нада нарисовать график как и про распределение по скоростям, тока написать f(E_k)./ Постоянная Больцмана k=R/N_A=1,38*10^-23Дж/К часто использ в уравнении состояния ИГ.(p=RT/V_m=kN_AT/V_m=knT, хде N_A/V_m=т(концентрация молк)) Она связывает температуру в энергетических единицах с температурой в Кельвинах. Физический смысл температуры: температура- мера средней кинетической энергии поступательного движения молекул.P=2/3E_Kn=2/3*3/2kT=nkT- закон Авогадро.Молекуляр физ и термодинамика – разделы, изуч макроскопич процессы в телах, связ с огромн числом содержащихся в телах атомов и молек. Для исследования этих процессов прим: статистический метод и термодинамич. Статистич лежит в основе молекулярной физики. Молекуляр физ – физика, изуч строение и свойства вещ-ва исходя из молекуляр-кинетич представлений, оновывающ на том, что все тела состоят из молекул, нах-ся в непрерывном движении. Процессы, изуч молк.физ.явл результатом действия огромн числа молекул. Свойства болш числа молк отличны то cв каждой молек и подчин статистическим закономерностям. Метод основан на том св макроскопич сис в конечном счёте опред свой-ми частич сис, особенностями их движения и усредненными значениями динамич хар-к этих частиц.

5.6. Основн уравнение МКТ. Уравнение Менделеева-Клапейрона. З-н Дальтона. Пусть в сосуде в виде куба со стороной l находится N молекул. Рассмотрим движение одной из молекул. Пусть молекула движется из центра куба в одном из 6 возможных направлений (рис.1) , например параллельно оси Х со скоростью v. Ударяясь о стенку А куба молекула оказывает на него давление (см. рис. 2). Найдем его. Согласно второму закону Ньютона сила д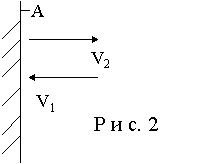 авления , где . Предполагая, что происходит абсолютно упругий удар, имеем v₁=v₂=v. Изменение импульса . Молекула вернется в исходное состояние ( в центр куба) спустя время dt=(0.5l+0.5l)/v=l/v. В итоге получаем выражение для силы давления, оказываемого на стенку сосуда одной молекулой .(10)Если число молекул в сосуде N, то к cтенке А движется в среднем N/6 молекул и они создают среднюю силу давления на стенку ,(11) где <v ²> - cредний квадрат скорости молекул [cм. формулы (17), (18)]. Давление, оказываемое на стенку сосуда, площадь которой S=l², (12) Учитывая, что N/l³=N/V=n, т.е. равно концентрации молекул, а также, что (13)-средняя кинетическая энергия поступательного движения молекулы газа, получаем из (12) основное уравнение молекулярно-кинетической теории идеального газа . (14) Такое же давление производят молекулы на другие стенки сосуда, поскольку молекулы газа движутся хаотически и не имеют какого-либо преимущественного направления движения. Итак, согласно (14) давление на стенки сосуда определяется произведением концентрации молекул n на их среднюю кинетическую энергию поступательного движения <W_к>.

Между параметрами газа сущ связ – Ур-е состояния В общем виде: f(p,V,T)=0, каждая из переем явл функцией двух других.В соответствии с з-ми Гей-Люссака и Мариотта: p₁V₁/T₁=p₂V₂/T₂ т.к. состояния 1и2 выбраны произволно, то для данной массы газа велич pV/T постоянна. pV/T=R=const., R-газовая постоянная. Это есть уравнение Клапейрона. Уравнению pV_m=RT удовлетвор лишь ИГ и оно явл Ур-ем состоян ИГ, наз уравнен Клапейрона-Менд-ва pV=m/M*RT=vRT, где v=m/M число молей.

Закон Дальтона. Давление смеси ИГ равно сумме парциальных давлений входящих в ней газов: p=p₁+…+p_n, где p – парциальные давления, давления котор оказывали бы газы смеси, если бы они одни занимали объём, равный объёму смеси при той же температуре.

5 .7. ИГ в поле тяготения. Барометрическая формула. Закон Больцмана для распределения частиц во внеш потенциальном поле. Распределение Максвелла-Больцмана для молекул ИГ. Барометрическая формула. Распределение Больцмана При выводе уравнения (14) предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы газа находятся в поле тяготения Земли, поэтому их концентрация с в ысотой уменьшается. Рассмотрим газ в сосуде (см. рис. 3). Если атмосферное давление на высоте h равно Р, то на высоте h+dh оно равно Р+dP (при dh>0 dP<0, т.к. давление с высотой убывает). Разность давлений Р и Р+dP равна весу газа, заключенного в объеме цилиндра высотой dh с основанием 1 м²: Р -(Р+dP)= gdh, где  - плотность газа. Следовательно, dP= -gdh. (19) Воспользовавшись уравнением Клапейрона-Менделеева РV= RT , находим, что . Подставив это выражение в (19), получим или . (20) Интегрируя (20) от h=0 до h находим, *(-1). Проведя потенцирование получим барометрическую формулу. , (21) где m₀=M/N_A, k=R/N_A. формула была впервые установлена в 1821 г. Лапласом.

А нализ барометрической формулы (21) показывает, что чем больше молярная масса М газа, тем быстрее его давление убывает с высотой. Поэтому атмосфера по мере увеличения высоты все более обогащается легкими газами. Следует иметь в виду, что применимость формулы (21) к реальной атмосфере несколько ограничена, поскольку атмосфера в действительности не находится в тепловом равновесии и ее температура меняется с высотой. Тем не менее ее используют, определяя высоту по изменению давления.Формулу (21) можно преобразовать, если воспользоваться выражением (9) Р=nkT , (22) где m₀gh=W_п - потенциальная энергия молекулы в поле тяготения, т.е. .(23) Больцман доказал, что формула (21) справедлива в случае потенциального поля любой природы (т.е. не только поля тяготения). В связи с этим функцию (23) называют распределением Больцмана. Из него следует, что при постоянной температуре плотность газа больше там, где меньше E_p его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического движения, то распределение Больц справедливо в любом внешнем потенциальном поле, а не только в поле силы тяжести.

В 1866 г. Больцман (1844-1906 г.) вывел более общее распределение, включающее распределение Максвелла, которое называется распределением Максвелла-Больцмана

(34), где - импульс частицы, в частности молекулы газа, - радиус-вектор, характеризующий положение частицы, p²/2m=W_к - кинетическая энергия частицы, - потенциальная энергия частицы. Распределение (34) можно записать в виде распределения по полной энергии Е частиц f(E)=Aexp(-E/kT), (35) где E=W_к+W_п - полная энергия частицы.

5 .8. Степени свободы молекул. Распределение энергии по степеням свободы. Внутренняя энергия ИГ. Важной хар тдс(термодинам сис)-её внутренняя энергия U – энергия хаотического движения микрочастич сис, (молек, 0атомов, ядер) Это однозначная функция тд состояния сис. Числа степеней свободы - числанезависимых перемен (координат) полностью определяющих положение сис в пространстве. Одноатомный газ рассматривают как м.т., которой приписывают 3 степени свободы. (рис а). Энергию вращат движения можно не учитывать(r→0, J=mr²→0, ) В классич мех-ке молк 2х атомн газа рассматр как совокуп 2х м.т. – атомов, жёстко связ-х недеформиров связью. Эта имеет кроме 3х степ св поступ движения ещё 2 вращат (i=5). 3х атомная молек&моногоатомн имеют 6 ст. св(i-6) Всегда в молекуле 3 ст.св. всегда поступательные. Ни одна не имеет преимуществ, в среднем на каждую по 1/3 энергии. <E₁>=1/3<E₀>=0,5kT. З-н Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящ-ся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем E_k=kT/2, а на каждую колебательную – в сред kT(т.к. ещё есть и потенциальная энергия, причем E_k≈ Ep. →<E>=i/2*kT, хде i=i_пост+i_вращ+2i_{колебат.} Т.к. в ИГ взаим потенц энер молек=0, то внутр энерг, отнесённая к одному молю газа, будет равна сумме кинет энер N_A молек: U_m=i/2*kTN_A=i/2*RT, если есть v=m/M, То U=v*i/2*RT=m/M*i/2*RT.

U=v*i/2*RT=m/M*i/2*RT.

5 .9. работа и теплота как две формы обмена энергией между ТДС. U=i/2*m/M/RT способ изменения U: в процессе работы над ТДС. Работа в ТД – процесс, в ходе которого измен внктр энергия ТДС за счёт энергии упорядоченного движения др тел или частей. Мерой работы как физ процесса явл сама работа.dA=Fdrcos0⁰=Fdr=pSdr=pdV, полная работа Результат определ хар-м зависимости между давлением и V газа. Производственную работу см на графике(давление газа при его расширении )При увелич V на dV, совершаемая газом работа равна pdV, т.е.опред заштрих площадью. Полная работа ограничена будет кривой p=f(V) и вертик прямыми. Графич можно изобраз тока равновесные процессы, т.е. те котор происходят медленно.

Р абота при круговом процессе. Круговой ТД процесс – процесс при котор сис пройдя ряд состояний, возвращается в исходное. Если работа идёт по часовой стрелке(прямой), то положительна, против(обратный) – отрицательна.

Теплопередача – процесс изменения внутренней энергии ТДС за счёт внутр энергии др тел.

1)теплопроводность. Конвекция – нагревание изменение внутр энерг за счёт направленных потоков(Н-р батареи в комнате).

2)электромагнитное излучение.

5.10. первое начало термодинамики(ПНТ) для круговых и не круговых процессов. Допустим, что некоторая термодинамическая система (например, газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U₁, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U₂, совершила работу А над внешней средой, т.е. против внешних сил. В этом случае Q=U₂-U₁+A или Q=U+A.(4)Уравнение (4) выражает ПНТ: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Для бесконечно малых процессов выражение (4) записывают в дифференциальной форме dQ=dU+dA или в более корректной форме

,(5)поскольку только dU является полным дифференциалом, а Q и А полными дифференциалами не являются. количество теплоты - в джоулях (Дж).Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии U=0. Тогда, согласно (4) А= Q , т.е. вечный двигатель первого рода, который совершал бы большую работу, чем сообщенная ему извне энергия, не возможен. Это одна из формулировок первого начала термодинамики.

Рассм ТДС, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия. Внутренняя энергия закрытой системы (т.е. системы, которая не обменивается веществом с внешней средой) может изменяться качественно различными способами:

1. Путем совершения работы внешними телами над системой, например, при сжатии газа температура его повышается и, следовательно, изменяется (увеличивается) его внутренняя энергия.

2. Путем теплообмена, т.е. процесса обмена внутренними энергиями при контакте тел с различными температурами. Энергию, передаваемую от одних тел к другим в процессе теплообмена, называют теплотой.

Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энергия механического движения может превращаться в энергию теплового движения и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии. Применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных.

1е начало ТД-частный случай з-на save энергии в примен тепловых процессов.

• Ни одна ТДС неможет соверщ работу без получ энергии из вне.

• Неможет сов работу больше энергии из вне.

A _1a2c1=Q_1a2c1; A_1b2c1=Q_1b2c1; Q_1a2+Q_2c1=A_1a2+A_2c1; Q_1B2+Q_2c1=A_1B2+A_2c1; Q_1a2-Q_1B2=A_1a2-A_1B2; Q_1a2-A_1a2=Q_1B2-A_1B2=const. Q-A=∆U C точки зрения ТД U – ФВ измен которой при любом процессе при переходе из состояния 1 в 2 измер разностью кол-ва тепла, получ в ходе этого процесса и работы, соверш этим процессом. Кол-во теплоты получ сис идёт на совершение работы и изменения её U.

5.11. Теплоёмкость в ТД. Полная, молярная и удельная теплоёмкости., C_уд=QM/mT; С=Q/t.

Теплоёмкость –СФВ хар связь между кол-м энергии, получ ТДС в форме Й или A и измен её t. Удельная теплоемкость вещества - величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: , Дж/(кгК). (9) Молярная теплоемкость С_m - величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К: , Дж/(моль*К). (10) где =m/M - количество молей вещества. Для ПНТ: C_mdT=dU_m+pdV_m. если газ нагрев при пост V, то A внеш сил=0 и энерг идёт на увелич его U: C_V=dU_m/dT_, dU_m=i/2*RdT→C_V=iR/2. ежели газ нагрев при P=const C_p=dU_m/dT+pdV_m/dT → C_p=C_V+R – это уравнение Майера. Оно показывает, что C_p всегда >С_V на величину R (при нагрев газа при пост Р треб ещё доп кол-во теплоты на соверш работы расширения газа, т.к. постоянство давления обеспеч ↑V → С_p=(i+2)/2*R; γ=C_p/C_V=i(+2)/ ТЕПЛОЕМКОСТЬ - величина, равная отношению количества теплоты δQ, сообщаемого телу (системе) при бесконечно малом изменении его состояния в каком-либо процессе, к соответствующему изменению температуры T этого тела: C=δQ/dT. Отношение теплоемкости к массе тела m называется удельной теплоемкостью: c = C/m, а отношение теплоемкости к количеству вещества - молярной теплоемкостью: C_m=Mc=MC/m, где M - молярная масса вещества. Теплоемкость зависит от химического состава вещества, условий, в которых оно находится, процесса теплопередачи. Например, в адиабатном процессе C = 0, в изохорическом процессе C=C_v в изобарическом процессе и в изотермическом процессе C= ±∞. В общем случае теплоемкость - функция температуры.[3]