3.6. Работа и мощность электротока. З-н джоуля-ленца.

Проводник нагревается, если по нему протекает электрический ток. И по з-ну save энергии dQ=dA. Джоуль и Ленц установили, что количество выделившегося тепла Q = I Rt, (28) где I - ток, R - сопротивление, t - время протекания тока. Легко доказать, что Q = I Rt = UIt = U ² t/R = qU, (29) где q = It - электрический заряд.

Если ток изменяется со временем (т. е. в случае непостоянного тока), то

Q = = , (30) где i - мгновенное значение тока. Нагревание проводника происходит за счет работы, совершаемой силами электрического поля над носителями заряда. Эта работа A = qU = UIt =I Rt = U t / R . (31) Работа А, энергия W , количество тепла Q [Дж].Работа - Так как мощность характеризует работу, совершаемую в единицу времени, т.е. Р =dA/dt, то P = UI = I²R = U²/ R . (32)Мощность измеряется в ваттах: 1 Вт = 1 Дж / 1 с Формулы (31) и (32) позволяют рассчитать полезную работу и полезную мощность. Затраченная работа и мощность определяется по формулам A = q = It = I ²(R + r)t = t. (33)

P = = I = I ²(R + r) = . (Отношение полезной работы (мощности) к затраченной характеризует КПД источника = = = . (35) Из (35) следует что при R  0,   0 ; R  ,  1.Но при R ток I 0 и поэтому А О и Р 0.Определим величину R , при котором выделится максимальная мощность. Легко показать, что это наступает при R = r, тогда P_MAКС=I R = = , (36) КПД в этом случае будет 50%.

3.7. РАЗВЕТВЛЕНИЕ ЦЕПИ . ПРАВИЛО КИРХГОФА И ИХ ПРИМЕНЕНИЕ К РАСЧЁТУ ЭЛ ЦЕПЕЙ. Узел: любая точка разветвления цепи, в которой сходится не менее 3х проводов СС током. Ток входящий в узел, считается положительным, а ток выходящий – отриц. В основе расчета электрических цепей лежат два правила Кирхгофа:

1) АЛГЕБРАИЧЕСКАЯСУММА ТОКОВ, СХОДЯЩИХСЯ В УЗЛЕ, РАВНА НУЛЮ, т. е. . (39) , .2) В ЛЮБОМ ЗАМКНУТОМ КОНТУРЕ АЛГЕБРАИЧЕСКАЯ СУММА НАПРЯЖЕНИЙ НА ВСЕХ УЧАСТКАХ ЭТОГО КОНТУРА РАВНА АЛГЕБРАИЧЕСКОЙ СУММЕ ЭДС, ВСТРЕЧАЮЩИХСЯ В ЭТОМ КОНТУРЕ При этом также следует придерживаться правила знаков: токи, текущие вдоль выбранного направления обхода контура считаются положительными, а идущие против направления обхода - отрицательными. Соответственно положительными считаются ЭДС тех источников, которые в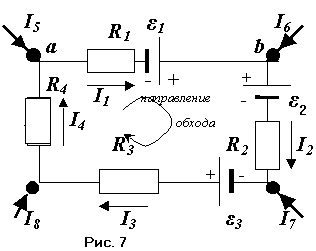 ызывают ток, совпадающий по направлению с обходом контура (см. рис.7), где обозначает направление обхода контура. Применим правила Кирхгофа для расчета электрической цепи(рис7). Для этого нужно записать (m-1) уравнений для основании первого правила Кирхгофа и еще одно уравнение для единственного здесь замкнутого контура, используя второе правило Кирхгофа и принимая во внимание направления ЭДС, токов в ветвях и обхода контура:

I , I I

4.1 Магнитное поле. Индукция магнитного поля. Силовые линии магнитного поля и их свойства.

Взаимодействие проводников с током обусловлено возникновением вокруг них магнитного поля. Магнитное поле возникает вокруг проводника с током всегда, даже если нет другого проводника и отследить действие поля таким способом нельзя.

Количественной характеристикой магнитного поля служит специальная физическая величина - напряженность магнитного поля H. С напряженностью связана также еще одна характеристика магнитного поля - индукция В. Между ними существует соотношение:

B=mm0H,

m - магнитная проницаемость вещества.

Индукция и напряженность являются векторами.

Силовые линии, линии, проведённые в каком-либо силовом поле (электрическом, магнитном, гравитационном), касательные к которым в каждой точке пространства совпадают по направлению с вектором, характеризующим данное поле (напряжённостью электрического или гравитационного полей, магнитной индукцией). Изображение силовых полей с помощью С. л. — частный случай изображения любых векторных полей с помощью линий тока. Т. к. напряжённости полей и магнитная индукция — однозначные функции точки, то через каждую точку пространства может проходить только одна С. л. Густота С. л. обычно выбирается так, чтобы через единичную площадку, перпендикулярную к С. л., проходило число С. л., пропорциональное напряжённости поля (или магнитной индукции) на этой площадке. Т. о., С. л. дают наглядную картину распределения поля в пространстве: густота С. л. и их направление характеризуют величину и направление напряжённости поля. С. л. электростатического поля всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). С. л. вектора магнитной индукции всегда замкнуты, т. е. магнитное поле является вихревым. Железные опилки, помещенные в магнитное поле, выстраиваются вдоль С. л.; благодаря этому можно экспериментально определять вид С. л. магнитной индукции. Вихревое электрическое поле, порождаемое изменяющимся магнитным полем, также имеет замкнутые С. л.