2.6 Работа сил электростатического поля. Циркуляция вектора напряженности электрического поля.

Работа перемещения заряда в поле. Точечный заряд Q₀ перемещается в поле заряда Q вдоль произвольной траектории: . Работа при перемещении заряда Q₀ из точки 1 в точку 2:

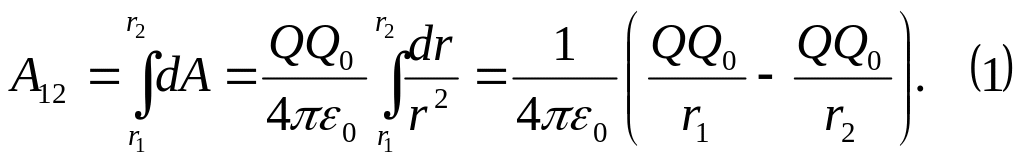
А₁₂ не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Работа перемещения заряда во внешнем электростатическом поле по любому замкнутому контуру L, согласно (1): . Циркуляция вектора . Если переносим заряд единичный, то элементарная работа сил поля на пути равна , где - проекция вектора на направление элементарного перемещения. Интеграл называется циркуляцией вектора напряженности. - теорема о циркуляции вектора . Силовое поле, обладающее таким свойством, называется потенциальным (эта формула справедлива только для электростатического поля).

2.7 Потенциал электростатического поля. Разность потенциалов. Эквипотенциальные поверхности.

Потенциальная энергия заряда (U). работа консервативных сил совершается за счет убыли потенциальной энергии, т.е. А₁₂ можно представить как разность потенциальных энергий заряда Q₀ d в начальной и конечной точках поля заряда Q: . Потенциальная энергия заряда Q₀, находящегося в поле заряда Q на расстоянии r от него, равна: . Если поле создается системой n точечных зарядов, то потенциальная энергия U заряда Q₀?, находящегося в этом поле, равна сумме его потенциальных энергий U_i, создаваемых каждым из зарядов в отдельности: . Потенциал в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в данную точку: .

1В – потенциал такой точки поля

э в которой заряд в 1Кл обладает потенциальной энергией 1Дж. 1В = 1Дж/Кл. Потенциал поля точечного заряда: . Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2. приравняв 1 и 2 получим: , где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения. Потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки в бесконечность.

2.8 Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.

Напряженность как градиент потенциала. Работа по перемещению единичного точечного положительного 0заряда из одной точки в другую вдоль оси X при условии, что точки расположены бесконечно близко друг к другу и x₂ – x₁ = dx, равна . Та же работа равна . Приравняв оба выражения получим: , где символ частной производной подчеркивает, что дифференцирование производится только по X. Повторив аналогичные рассуждения для осей Y и Z, имеем , или , ( - единичные векторы координатных осей x,y,z ). Знак минус показывает, что вектор направлен в сторону убывания потенциала. Эквипотенциальные поверхности – поверхности, во всех точках потенциал φ имеет одно и тоже значение. Используются для графического изображения распределения потенциала. Точечный заряд: линии вектора и эквипотенциальные поверхности (см. рис.).

Вектор : 1) всегда перпендикулярен эквипотенциальным поверхностям; 2) всегда направлен в сторону убывания потенциала. Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.

2.9 Расчет потенциала и разности потенциалов для электростатических полей (электростатических полей сферы из металла или диэлектрика; равномерно заряженной по поверхности или объему; цилиндра из металла или диэлектрика равномерно заряженного поверхности ил объему; нити (стержня) равномерно заряженной по длине, точечного заряда).

Поле равномерно заряженной сферической поверхности. Радиус сферы R, общий заряд Q. При r > R , . Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра сферы (r₁ > R, r₂ > R), равна: . Если принять , то потенциал поля вне сферической поверхности задается выражением .

Поле равномерно заряженного бесконечного цилиндра. Радиус цилиндра R, заряжен с линейной плотностью τ, вне цилиндра (r > R) напряженность определяется формулой , следовательно разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от оси заряженного цилиндра (r₁ > R , r₂ >R), равна .
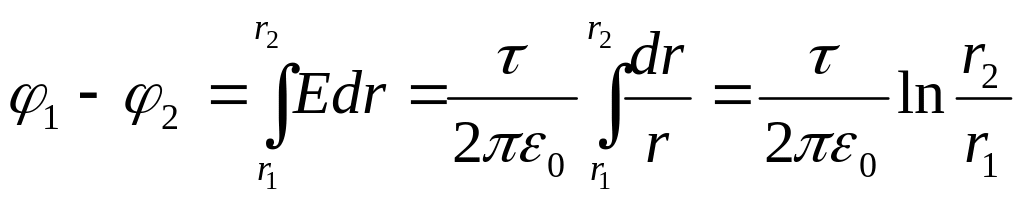