Энергия упругой волны

Процесс распространения упругой волны связан с вовлечением в колебательное движение частиц среды. Любое же колеблющееся тело обладает энергией, следовательно, можно говорить о передаче энергии колебательного движения от одних частиц среды другим. Иными словами, упругая волна переносит энергию.

П усть в некоторой области пространства вдоль оси ОХ распространяется плоская продольная волна. Ее уравнение имеет вид

Рассмотрим малый элемент объема dV среды, в которой распространяется волна.

Частицы среды, находящиеся в выделенном нами объеме, двигаются, участвуя в колебательном движении, а значит, они обладают кинетической энергией.

П оскольку выбранный нами элемент объема очень мал, можно считать, что все его точки имеют одинаковые скорости. Тогда кинетическая энергия выделенного объема может быть рассчитана как

г де  - плотность упругой среды, v – скорость всех точек выделенного нами объема. Скорость колебательного движения может быть найдена как производная от смещения по времени:

Тогда кинетическая энергия выделенного объема будет равна:

Р 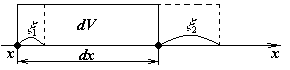аспространение волны связано с деформацией упругой среды. Величина относительной деформации выделенного нами участка равна

П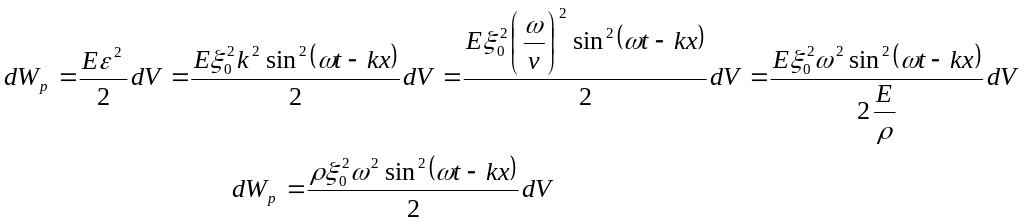 отенциальная энергия упругой деформации выделенного объема dV:

Интересно!! Кинетическая и потенциальная энергии выделенного объема упругой среды (он, кстати, был выбран произвольно) одинаковы, более того, они меняются в одной фазе (в отличие от кинетической и потенциальной энергий колеблющегося маятника).

П олная энергия выделенного участка

П лотность энергии волны (энергия единицы объема)

Видно, что плотность энергии любого участка среды, в которой распространяется волна, меняется с течением времени – переносится, передается от одних частиц другим.

С реднее за период значение квадрата синуса равно ½, следовательно, средняя за период плотность энергии волны будет равна

Обычно, для характеристики волновых процессов пользуются понятием интенсивности волны. Интенсивностью волны называют энергию, переносимую волной за 1 секунду через поверхность площадью в 1 м², расположенную перпендикулярно скорости распространения волны.

Р ассчитаем интенсивность волны.

Через площадку dS за время dt будет перенесена энергия, заключенная в объеме цилиндра с основанием dS и высотой vdt. Поскольку размеры цилиндра очень малы, можно считать плотность энергии в каждой его точке одинаковой. Тогда: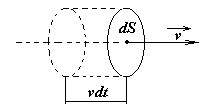

Интенсивность волны прямо пропорциональна:

1. плотности среды;

2. квадрату амплитуды волны (эта зависимость характерна для волнового процесса любой природы) ;

3. квадрату частоты волны;

4. скорости волны.

Если волна плоская, то ежесекундно в колебательное движение вовлекается одинаковое количество частиц, волновой фронт проходит через поверхность одинаковой площади. Это значит интенсивность волны везде одинаковая, следовательно, амплитуды колебания всех точек среды одинаковые.

Е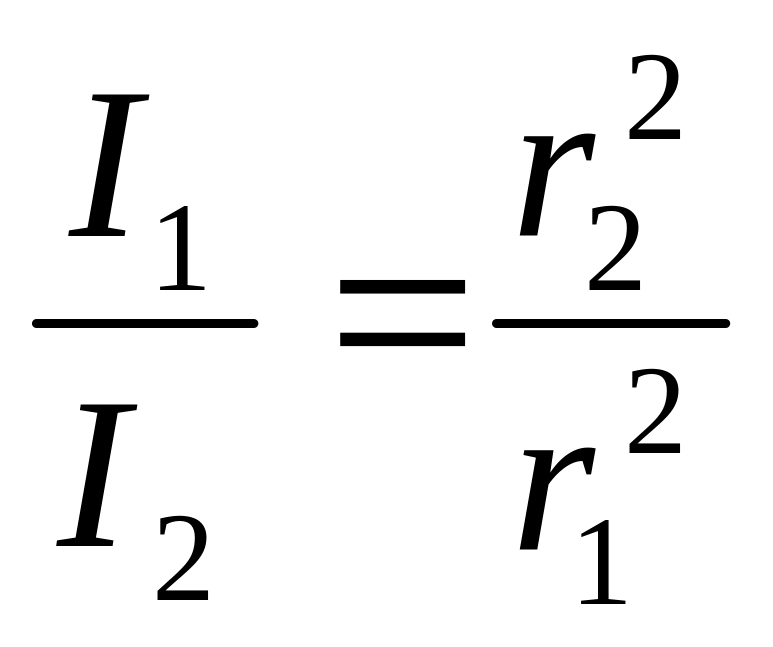 сли волна сферическая, то волновыми поверхностями для нее будут сферы. Энергия, переносимая волной за секунду через каждую сферу одинакова, а вот интенсивность волны будет убывать обратно пропорционально площади поверхности, т.е. обратно пропорционально расстоянию до источника волны:

Т огда амплитуда колебания точек в сферической волне будет убывать обратно пропорционально расстоянию до источника волны:

Выводы, полученные нами, справедливы и для поперечной волны.

Мы рассмотрели идеальный случай незатухающей волны. В реальной плоской волне амплитуда и интенсивность убывают с расстоянием по закону

Энергия волны поглощается средой, в которой она распространяется.