Вопрос 5. Значение резонанса.

Вынужденные колебания и резонанс широко используются в технике, особенно в акустике, электротехнике, радиотехнике. Резонанс, в первую очередь, используется тогда, когда из большого набора колебаний разной частоты хотят выделить колебания определенной частоты. Резонанс используется и при изучении очень слабых периодически повторяющихся величин.

Однако, в ряде случаев резонанс – нежелательное явление, так как может привести к большим деформациям и разрушениям конструкций.

Примеры решения задач

1. Вынужденные колебания пружинного маятника под действием внешней синусоидальной силы.

К пружине жесткостью k = 10 Н/м подвесили груз массой m = 10 г и поместили систему в вязкую среду с коэффициентом сопротивления r = 0,1 кг/с. Сравните собственную и резонансную частоту системы. Определите амплитуду колебаний маятника при резонансе под действием синусоидальной силы с амплитудой F₀ = 20 мН.

Решение.

1. Собственная частота колебательной системы – это частота свободных колебаний в отсутствии трения. Собственная циклическая частота равна , частота колебаний .

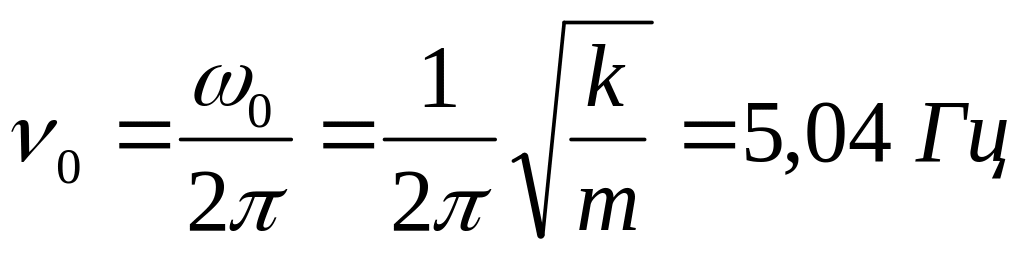2. Резонансная частота – это частота внешней вынуждающей силы, при которой амплитуда вынужденных колебаний резко возрастает. Резонансная циклическая частота равна , где - коэффициент затухания, равный .

Таким образом, резонансная частота равна . Нетрудно видеть, что резонансная частота меньше собственной! Также видно, что чем меньше трение в системе (r) , тем ближе резонансная частота к собственной.

3. Резонансная амплитуда равна .

2. Резонансная амплитуда и добротность колебательной системы.

Условие

К пружине жесткостью k = 10 Н/м подвесили груз массой m = 100 г и поместили систему в вязкую среду с коэффициентом сопротивления r = 0,02 кг/с. Определите добротность колебательной системы и амплитуду колебаний маятника при резонансе под действием синусоидальной силы с амплитудой F₀ = 10 мН. Найдите отношение резонансной амплитуды к статическому смещению под действием постоянной силы F₀ = 20 мН и сравните это отношение с добротностью.

Решение.

1. Добротность колебательной системы равна , где - логарифмический декремент затухания.

Логарифмический декремент затухания равен .

Находим добротность колебательной системы .

2. Резонансная амплитуда равна .

3. Статическое смещение под действием постоянной силы F₀ = 10 мН равно .

4. Отношение резонансной амплитуды к статическому смещению под действием постоянной силы F₀ равно

Н етрудно видеть, что это отношение совпадает с добротностью колебательной системы

3. Резонансные колебания балки

Под действием веса электромотора консольная бака, на которой он установлен, прогнулась на . При каком числе оборотов якоря мотора может возникнуть опасность резонанса?

Решение

1. Корпус двигателя и балка, на которой он установлен, испытывают периодические толчки со стороны вращающегося якоря мотора и, следовательно, совершают вынужденные колебания с частотой следования толчков.

Резонанс будет наблюдаться при совпадении частоты следования толчков с собственной частотой колебания балки с мотором . Необходимо найти собственную частоту колебаний системы балка – мотор.

2. Аналогом колебательной системы балка – мотор может служить вертикальный пружинный маятник, масса которого равна массе мотора. Собственная частота колебаний пружинного маятника равна . Но жесткость пружины и масса мотора не известны! Как быть?

3. В положении равновесия пружинного маятника сила тяжести груза уравновешивается силой упругости пружины

4. Находим вращения якоря двигателя, т.е. частоту следования толчков